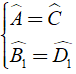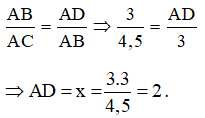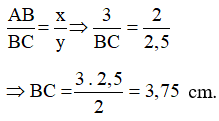TOP 40 câu Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác (có đáp án 2023) - Toán 8

Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 7: Trường hợp đồng dạng thứ ba của tam giác có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 7.

1 2,039 16/02/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 8 Bài 7: Trường hợp đồng dạng thứ ba của tam giác

Bài giảng Trắc nghiệm Toán 8 Bài 7: Trường hợp đồng dạng thứ ba của tam giác

Bài 1: Tam giác ABC có $\hat{A} = 2 \hat{B}$ , AC = 16cm, BC = 20cm. Tính độ dài cạnh AB.

A. 18cm

B. 20cm

C. 15cm

D. 9cm

Hiển thị đáp án

Đáp án: D

Giải thích:

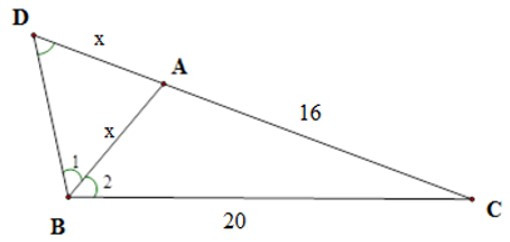
Trên tia đối của tia AC lấy điểm D sao cho AD = AB.

Tam giác ABD cân tại A

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 3)

Bài 2: Cho tam giác ABC vuông tại A có: AB = 5, AC = 12. Trên cạnh BC lấy điểm M

sao cho BM = $\frac{5}{13}$ BC. Qua M kẻ đường thẳng vuông góc với AC tại N. Độ dài MN là:

A. $\frac{12}{13}$

B. $\frac{45}{13}$

C. $\frac{40}{13}$

D. 12

Hiển thị đáp án

Đáp án: C

Giải thích:

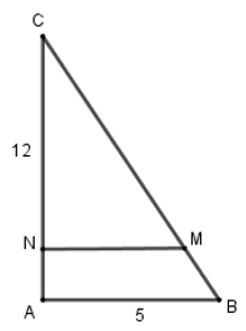
Tam giác ABC vuông tại A, theo định lí Pi-ta-go ta có:

BC² = AB² + AC²

=> BC² = 5² + 12² = 169

=> BC = 13

BM = BC = .13 = 5

=> CM = 13 - 5 = 8.

Xét ΔCMN và ΔCBA có:

N = A = 90⁰(gt)

Góc C chung

=> ΔCMN ~ ΔCBA (g - g)

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 6)

Bài 3: Cho hình thang vuông ABCD ( $\hat{A} = \hat{D} = 90^{0}$ )

có BC BD, AB = 4cm, CD = 9cm. Độ dài BD là:

A. 8cm

B. 12cm

C. 9cm

D. 6cm

Hiển thị đáp án

Đáp án: D

Giải thích:

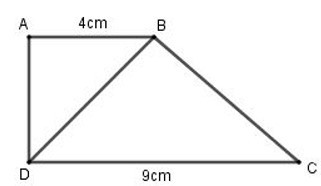
Xét tam giác ABD và BDC có:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 8)

=> BD² = AB.CD = 4.9 = 36

=> BD = 6.

Bài 4: Cho hai tam giác ABC và FED có $\hat{A} = \hat{F}$ , cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc - góc?

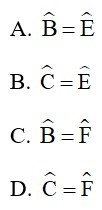
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 9)

Hiển thị đáp án

Đáp án: A

Giải thích:

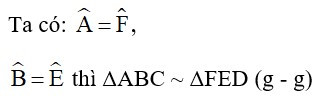
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 10)

Bài 5: Tính giá trị của x trong hình dưới đây:

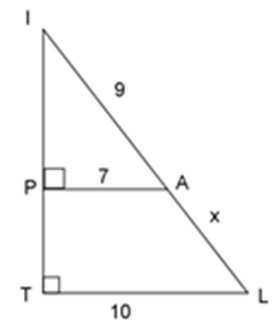
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 11)

A. x = 3

B.x = $\frac{27}{7}$

C. x = 4

D. x = $\frac{27}{5}$

Hiển thị đáp án

Đáp án: B

Giải thích:

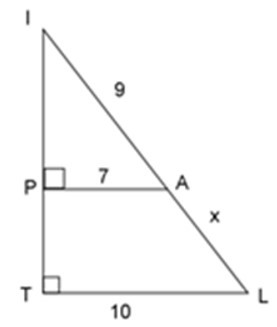
Xét ΔIPA và ΔITL ta có:

+) IPA = ITL = 90⁰

+) Góc TIL chung

=> ΔIPA ~ ΔITL (g - g)

=> $\frac{P A}{T L} = \frac{I A}{I L} \Leftrightarrow \frac{P A}{T L} = \frac{I A}{I A + A L}$

$\Leftrightarrow \frac{7}{10} = \frac{9}{9 + x}$

$\Leftrightarrow x = \frac{27}{7}$

Bài 6: Tam giác ABC có $\hat{A} = 2 \hat{B}$ , AB = 11cm, AC = 25cm. Tính độ dài cạnh BC.

A. 30cm

B. 20cm

C. 25cm

D. 15cm

Hiển thị đáp án

Đáp án: A

Giải thích:

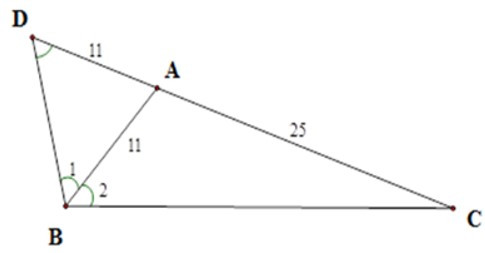
Trên tia đối của tia AC lấy điểm D sao cho AD = AB.

Tam giác ABD cân tại A

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 15)

Từ đó BC² = 25.36 suy ra BC = 5.6 = 30(cm)

Bài 7: Nếu 2 tam giác ABC và DEF có $\hat{A} = 70 °, \hat{C} = 60 °, \hat{E} = 50 °, \hat{F} = 70 °$ thì chứng minh được:

A.ΔABC ~ ΔFED

B. ΔACB ~ ΔFED

C. ΔABC ~ ΔDEF

D. ΔABC ~ ΔDFE

Hiển thị đáp án

Đáp án: A

Giải thích:

Xét ΔABC có:

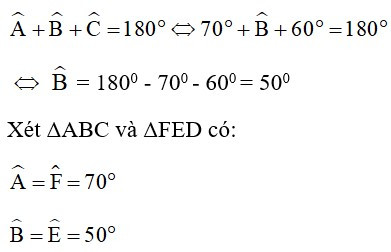
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 16)

=> ΔABC ~ ΔFED (g - g)

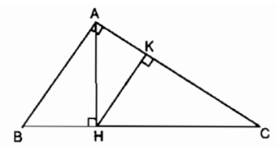
Bài 8: Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc $\hat{B C K} = \hat{A B M}$ .

1. Tam giác MBC đồng dạng với tam giác

A. MCK

B. MKC

C. KMC

D. CMK

Hiển thị đáp án

Đáp án: A

Giải thích:

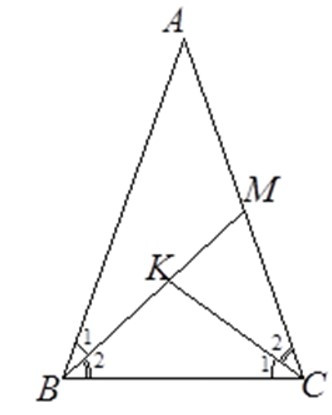
Tam giác ABC cân tại A

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 18)

Do đó ΔMBC ~ ΔMCK (g.g).

2. Tính MB.MK bằng

A. 2MC²

B. CA²

C. MC²

D. BC²

Hiển thị đáp án

Đáp án: C

Giải thích:

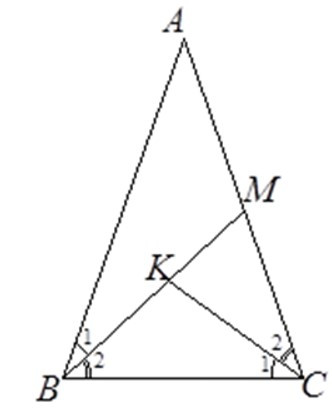
Vì ΔMBC ~ ΔMCK nên $\frac{M C}{M K} = \frac{M B}{M C}$ (hai cạnh tương ứng tỉ lệ)

Suy ra MC² = MB.MK

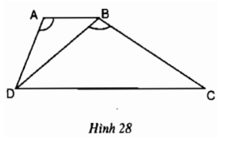
Bài 9: Cho hình thang ABCD (AB // CD) có góc $\hat{A D B} = \hat{B C D}$ , AB = 2cm, BD = $\sqrt{5}$ cmm, ta có:

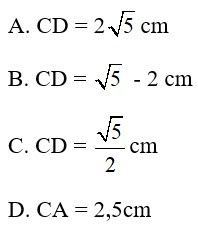
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 20)

Hiển thị đáp án

Đáp án: D

Giải thích:

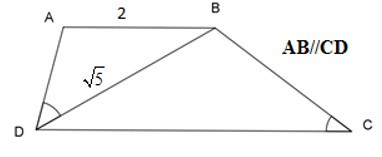
Vì AB // CD nên: $\hat{A B D} = \hat{B D C}$ (cặp góc so le trong)

Xét ΔADB và ΔBCD ta có:

$\hat{A B D} = \hat{B D C}$ (chứng minh trên)

$\hat{A D B} = \hat{B C D}$ (theo gt)

=> ΔADB ~ ΔBCD (g - g)

=> $\frac{A B}{B D} = \frac{D B}{C D} \Leftrightarrow \frac{2}{\sqrt{5}} = \frac{\sqrt{5}}{C D}$

$\Leftrightarrow C D = \frac{\sqrt{5} . \sqrt{5}}{2} = \frac{5}{2}$ = 2,5 cm

Bài 10: Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.

1. Chọn câu đúng.

A. ΔHBE ~ ΔHCD

B. ΔABD ~ ΔACE

C. Cả A, B đều đúng

D. Cả A, B đều sai

Hiển thị đáp án

Đáp án: C

Giải thích:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 1)

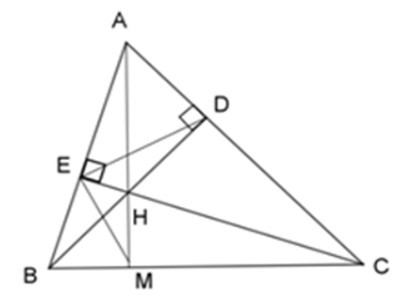
2. Chọn khẳng định sai.

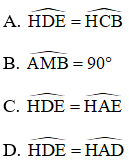
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 1)

Hiển thị đáp án

Đáp án: D

Giải thích:

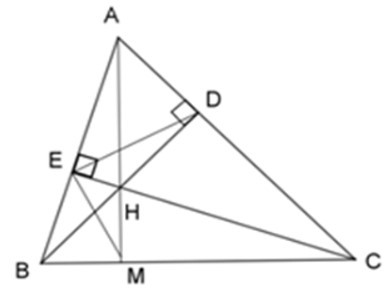
Theo cmt ta có: ΔHBE ~ ΔHCD

Xét ΔHED và ΔHBC ta có:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 27)

Từ (1) và (2) ta có: $\hat{H D E} = \hat{H A E}$ nên A, B, C đúng, D sai.

Bài 11: Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.

A. ΔBFE ~ ΔDAE

B. ΔDEG ~ ΔBEA

C. ΔBFE ~ ΔDEA

D. ΔDGE ~ ΔBAE

Hiển thị đáp án

Đáp án: C

Giải thích:

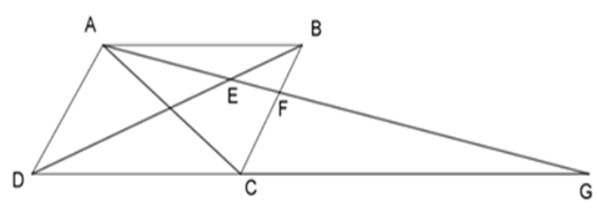
Có ABCD là hình bình hành nên: AD // BC, AB // DC

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 29)

=> ΔDGE ~ ΔBAE (g - g) hay ΔDEG ~ ΔBEA nên B, D đúng

Bài 12: Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?

A. ΔBGE ~ ΔHGI

B. ΔGHI ~ ΔBAI

C. ΔBGE ~ ΔDGF

D. ΔAHF ~ ΔCHE

Hiển thị đáp án

Đáp án: A

Giải thích:

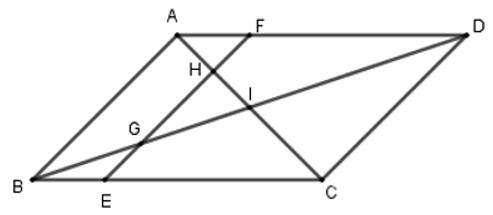
Có ABCD là hình bình hành nên: AD // BC, AB // DC

Xét ΔBGE và ΔDGF có:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 31)

Chỉ có A sai.

Bài 13: Nếu 2 tam giác ABC và DEF có $\hat{A} = \hat{D}, \hat{C} = \hat{F}$ thì:

A. ΔABC ~ ΔDEF

B. ΔCAB ~ ΔDEF

C. ΔABC ~ ΔDFE

D. ΔCBA ~ ΔDFE

Hiển thị đáp án

Đáp án: A

Giải thích:

Xét ΔABC và ΔDEF có:

$\hat{A} = \hat{D}$ (gt)

$\hat{C} = \hat{F}$ (gt)

=> ΔABC ~ ΔDEF (g - g)

Bài 14: Cho ΔABC có đường cao AD, CE và trực tâm H.

1. Chọn câu trả lời đúng nhất.

A. ΔADB ~ ΔCDH

B. ΔABD ~ ΔCBE

C. Cả A, B đều đúng

D. Cả A, B đều sai

Hiển thị đáp án

Đáp án: C

Giải thích:

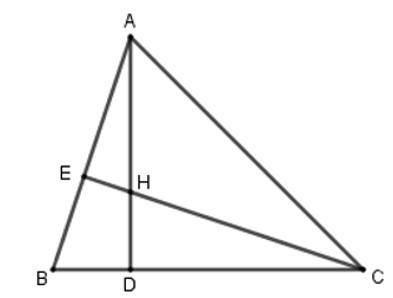
Xét tam giác ABD và CBE có:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 33)

Vậy A, B đều đúng

2. Chọn khẳng định sai.

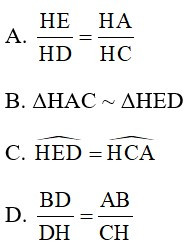
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 34)

Hiển thị đáp án

Đáp án: C

Giải thích:

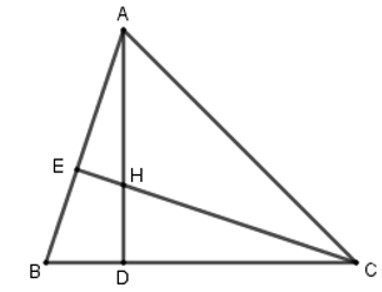
Theo câu trên, ΔADB ~ ΔCDH

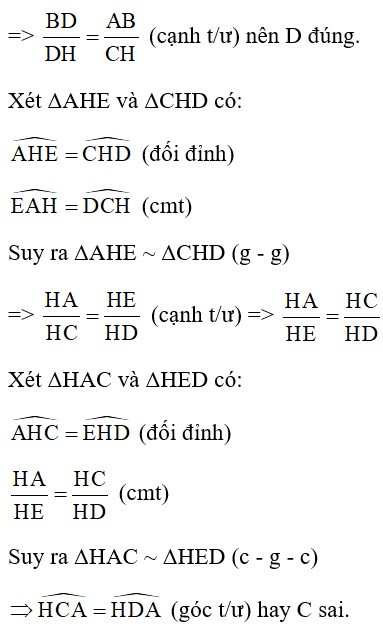
Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 36)

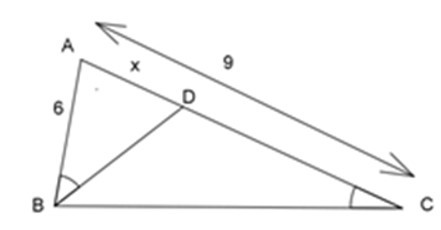
Bài 15: Cho hình bên biết AB = 6cm, AC = 9cm, $\hat{A B D} = \hat{B C A}$ . Độ dài đoạn AD là:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 37)

A. 2cm

B. 3cm

C. 4cm

D. 5cm

Hiển thị đáp án

Đáp án: C

Giải thích:

Xét ΔABD và ΔACB có:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 39)

Bài 16: Cho ΔABC cân tại A, M là trung điểm BC, BC = 2a

lấy D, E thuộc AB, AC sao cho $\hat{D M E} = \hat{A B C}$ . Tính BD.CE bằng

A. 2a²

B. 3a

C. a²

D. 4a²

Hiển thị đáp án

Đáp án: C

Giải thích:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 41)

Bài 17: Cho hình bên biết AB = 8cm, AC = 16cm, $\hat{A B D} = \hat{B C A}$ . Độ dài đoạn AD là:

A. 4cm

B. 8cm

C. 6cm

D. 5cm

Hiển thị đáp án

Đáp án: A

Giải thích:

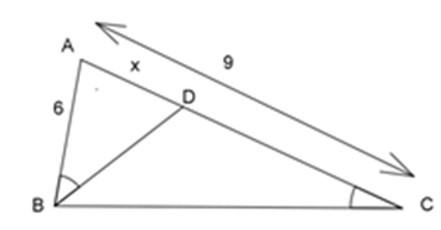
Xét ΔABD và ΔACB có:

A chuhng

ABD^ = BCA^ (gt)

=> ΔABD ~ ΔACB (g-g)

=> 4cm

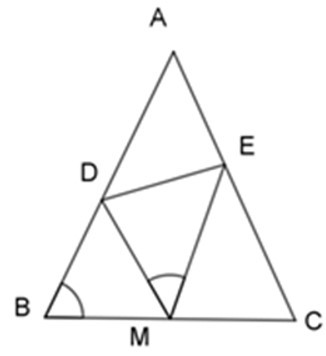
Bài 18: Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE. Chọn khẳng định đúng.

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 44)

Hiển thị đáp án

Đáp án: C

Giải thích:

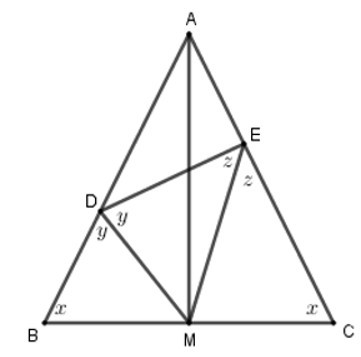
Tam giác ABC có: M là trung điểm của BC nên AM vừa là đường trung tuyến vừa là đường phân giác trong góc A.

Lại có: DM là ghân giác của góc BDE nên DM là phân giác ngoài góc D của tam giác ADE.

Tam giác ADE có phân giác trong AM cắt phân giác ngoài DM tại M nên EM là đường phân giác ngoài góc E hay EM là phân giác của góc DEC.

Vậy $\hat{D E M} = \hat{C E M}$ .

Bài 19: Cho 2 tam giác ABC và DEF

có $\hat{A} = 40 °, \hat{B} = 80 °, \hat{E} = 40 °, \hat{D} = 60 °$ . Chọn câu đúng.

A.ΔABC ~ ΔDEF

B. ΔFED ~ ΔCBA

C. ΔACB ~ ΔEFD

D. ΔDFE ~ ΔCBA

Hiển thị đáp án

Đáp án: D

Giải thích:

Xét ΔABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$

$\Rightarrow \hat{C} = 180 ° - 40 ° - 80 ° = 60 °$

$\Rightarrow \hat{C} = \hat{D}$

Tam giác DEF có: $\hat{D} + \hat{E} + \hat{F} = 180 °$

$\Rightarrow \hat{F} = 180 ° - 40 ° - 60 ° = 80 °$

Xét ΔABC và ΔFED có:

$\hat{A} = \hat{E} = 40 °$

$\hat{C} = \hat{D} = 60 °$

=> ΔABC ~ ΔEFD (g - g) hay ΔCBA ~ ΔDFE

Bài 20: Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE. Chọn kết luận đúng.

A. ΔBDM ~ ΔCME

B. ΔBDM ~ ΔEMC

C. ΔBDM ~ ΔCEM

D. ΔBDM ~ ΔECM

Hiển thị đáp án

Đáp án: A

Giải thích:

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 46)

Bài 21: Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC,

lấy D, E thuộc AB, AC sao cho $\hat{D M E} = \hat{A B C}$ . Góc BDM bằng với góc nào dưới đây?

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 42)

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: ΔBDM ~ ΔCME (cmt)

Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác có đáp án - Toán 8 (ảnh 43)

Bài 22: Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD (làm tròn đến chữ số thập phân thứ nhất)

A. 16cm

B. 12cm

C. 18cm

D. 20cm

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: Bài tập Các trường hợp đồng dạng của tam giác | Lý thuyết và Bài tập Toán 8 có đáp án

⇒ Δ CDB ∼ Δ ABE ( g - g )

⇒ CD/AB = BC/AE

hay CD/15 = 10/12 ⇔ CD = (10.15)/12 ⇒ CD = 18 ( cm )

Bài 23: Cho hình bình hành ABCD .Gọi E là trung điểm của AB, F là trung điểm của CD. Chọn câu trả lời đúng?

A. ΔAED ∽ ΔCFB

B. ΔADE ∽ ΔCFB

C. ΔAED ∽ ΔCBF

D. ΔADE ∽ ΔCFB

Hiển thị đáp án

Đáp án: A

Giải thích:

Vì ABCD là hình bình hành nên:

AB = CD (1)

Theo giả thiết:

AE = EB = $\frac{1}{2}$ AB (2)

DF = FC = $\frac{1}{2}$ CD (3)

Từ (1), (2) và (3) suy ra:

EB = DF và BE // DF (do AB // CD).

Suy ra: tứ giác BEDF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)

Suy ra: DE // BF.

Ta có: $\hat{A E D} = \hat{A B F}$ (đồng vị)

$\hat{A B F} = \hat{B F C}$ (so le trong)

Suy ra: $\hat{A E D} = \hat{B F C}$

Xét ΔAED và ΔCFB ta có:

$\hat{A E D} = \hat{B F C}$ (chứng minh trên)

$\hat{A} = \hat{C}$ (tính chất hình bình hành)

Vậy: ΔAED ∽ ΔCFB (g.g).

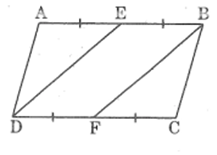
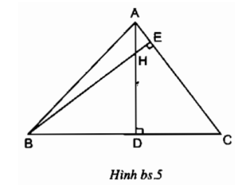
Bài 24: Tam giác vuông ABC có $\hat{A}$ = 90° và đường cao AH. Từ H hạ HK vuông góc với AC. Trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau?

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án

Đáp án: A

Giải thích:

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Ta có: $\hat{B A C} = \hat{A H C} = \hat{A H B} = \hat{A K H} = \hat{H K C} = 90^{o}$ .

$\hat{B} = \hat{H A C} = \hat{K H C}$ (do HK // AB và cùng phụ )

Và $\hat{C} = \hat{A H K} = \hat{B A H}$ .

Trong hình trên có 5 tam giác đồng dạng với nhau theo từng đôi một (theo trường hợp g.g) đó là:

ΔABC; ΔHBA; ΔHAC; ΔKAH; ΔKHC.

Bài 25: Hình thang ABCD (AB // CD) có AB = 2,5cm, AD = 3,5cm, BD = 5cm và $\hat{D A B} = \hat{D B C}$ .Tính độ dài BC.

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

A. 8cm

B. 10cm

C. 7cm

D. 5cm

Hiển thị đáp án

Đáp án: C

Giải thích:

Xét ΔABD và ΔBDC, ta có:

$\hat{D A B} = \hat{D B C}$ (gt)

$\hat{A B D} = \hat{B D C}$ (AB // CD, so le trong)

Suy ra: ΔABD ∽ ΔBDC (g.g)

b) Vì ΔABD ∽ ΔBDC nên: $\frac{A B}{B D} = \frac{A D}{B C} = \frac{B D}{D C}$

Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có:

$\frac{2, 5}{5} = \frac{3, 5}{B C} = \frac{5}{D C}$

$\Rightarrow B C = 3, 5 . \frac{5}{2, 5} = 7 (c m)$ .

Bài 26: Cho biết tam giác ABC có hai đường cao AD và BE cắt nhau tại H.

Trong hình có số cặp tam giác đồng dạng với nhau là:

A. 1 cặp

B. 6 cặp

C. 3 cặp

D. 4 cặp

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có 6 cặp tam giác đồng dạng là:

+ ΔBEC và ΔADC (vì $\hat{B E C} = \hat{A D C} = 90^{o}; \hat{ C} c h u n g$ )

+ ΔAHE và ΔBHD (vì $\hat{A E H} = \hat{B D H} = 90^{o}; \hat{A H E} = \hat{B H D}$ (hai góc đối đỉnh)).

+ ΔAHE và ΔACD (vì $\hat{A E H} = \hat{A D C} = 90^{o}; \hat{D A C} c h u n g)$

+ ΔAHE và ΔBCE (vì $\hat{A E H} = \hat{B E C} = 90^{o}; \hat{E A H} = \hat{E B C}$ (vì ΔAHE ∽ ΔBHD)).

+ ΔBDH và ΔBEC (vì $\hat{B E C} = \hat{B D H} = 90^{o}; \hat{E B C}$ chung).

+ ΔBDH và ΔADC (vì $\hat{B D H} = \hat{A D C} = 90^{o}$ ; $\hat{D B H} = \hat{D A C}$ (vì ΔAHE ∽ ΔBHD)).

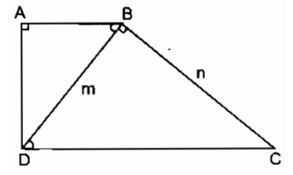
Bài 27: Hình thang vuông ABCD (AB // CD) có đường chéo BD vuông góc với cạnh BC tại B và có độ dài BD = m = 7,25cm. Hãy tính độ dài các cạnh của hình thang, biết rằng BC = n = 10,75cm

A. 11,29cm

B. 12,97cm

C. 18cm

D. 4,05cm

Hiển thị đáp án

Đáp án: B

Giải thích:

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Theo giả thiết ABCD là hình thang vuông và AB // CD, BD ⊥ BC nên ta có:

$\hat{D A B} = \hat{C B D} = 90 °$

$\hat{A B D} = \hat{B D C}$ (so le trong)

Do đó: ΔABD đồng dạng ΔBDC

$\Rightarrow \frac{A B}{B D} = \frac{A D}{B C} = \frac{B D}{D C} (1)$ .

Xét tam giác vuông DBC, theo định lí Py – ta – go, ta có:

$D C = \sqrt{B D^{2} + B C^{2}} = \sqrt{m^{2} + n^{2}}$

Từ dãy tỉ lệ thức (1), tính được:

$A B = \frac{B D^{2}}{D C} = \frac{m^{2}}{\sqrt{m^{2} + n^{2}}}; A D = \frac{B C . B D}{D C} = \frac{m n}{\sqrt{m^{2} + n^{2}}}$

Thay m = 7,25cm, n = 10,75 cm vào $D C = \sqrt{m^{2} + n^{2}}$ , ta được:

$D C = \sqrt{m^{2} + n^{2}} = \sqrt{{(7, 25)}^{2} + {(10, 75)}^{2}} = \sqrt{169, 125} \approx 12, 97 (c m)$

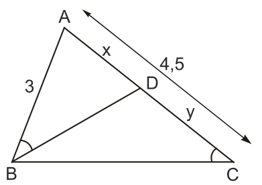
Bài 28: Cho biết AB = 3cm; AC = 4,5cm và. Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC.

Để học tốt Toán 8 | Giải toán lớp 8

A. 2cm

B. 4cm

C. 3,75cm

D. 2,5cm

Hiển thị đáp án

Đáp án: C

Giải thích:

Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC

+ Xét ΔABD và ΔACB có:

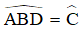
Để học tốt Toán 8 | Giải toán lớp 8

$\hat{A}$ chung

⇒ ΔABD Giải bài 25 trang 72 SGK Toán 8 Tập 2 | Giải toán lớp 8 ΔACB (g.g)

b) Theo a ta có: ΔABD Giải bài 25 trang 72 SGK Toán 8 Tập 2 | Giải toán lớp 8 ΔACB nên:

Để học tốt Toán 8 | Giải toán lớp 8

Suy ra: y = 4,5 – 2 = 2,5.

c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:

Để học tốt Toán 8 | Giải toán lớp 8

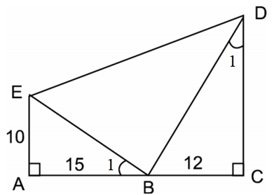
Bài 29: Cho biết . Cho biết AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD

Giải bài 37 trang 79 SGK Toán 8 Tập 2 | Giải toán lớp 8

A. 26,63cm

B. 18,03cm

C. 28,18cm

D. 21,63cm

Hiển thị đáp án

Đáp án: D

Giải thích:

Giải bài 37 trang 79 SGK Toán 8 Tập 2 | Giải toán lớp 8

Trong hình vẽ có tất cả ba tam giác vuông.

+ ΔABE vuông tại A.

+ ΔBCD vuông tại C.

Giải bài 37 trang 79 SGK Toán 8 Tập 2 | Giải toán lớp 8

Vậy ΔBED vuông tại B.

Áp dụng định lý Py – ta - go trong ΔABE vuông tại A ta có:

EB² = AE² + AB² = 10² + 15² = 325

⇒ EB = √325 ≈ 18,03 (cm).

+ Xét ∆ABE và ∆CDB có:

Giải bài 37 trang 79 SGK Toán 8 Tập 2 | Giải toán lớp 8

Suy ra: ∆ABE Giải bài 25 trang 72 SGK Toán 8 Tập 2 | Giải toán lớp 8 ∆CDB (g.g).

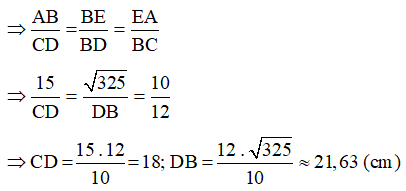
Giải bài 37 trang 79 SGK Toán 8 Tập 2 | Giải toán lớp 8

Bài 30: Cho hai tam giác ABC và FED có $\hat{A B C} = \hat{F E D}$ , cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc - góc?

A. $\hat{A C B} = \hat{F E D}$

B. $\hat{A B C} = \hat{F D E}$

C. $\hat{A C B} = \hat{F D E}$

D. $\hat{A C B} = \hat{D F E}$

Hiển thị đáp án

Đáp án: C

Giải thích: Xét hai tam giác ABC và FED có:

$\hat{A B C} = \hat{F E D}$ và $\hat{A C B} = \hat{F D E}$

=> $∆ A B C = ∆ F E D$ (g-g)

Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:

Trắc nghiệm Khái niệm về hai tam giác đồng dạng có đáp án

Trắc nghiệm Trường hợp đồng dạng thứ nhất của tam giác có đáp án

Trắc nghiệm Trường hợp đồng dạng thứ hai của tam giác có đáp án

Trắc nghiệm Trường hợp đồng dạng của tam giác vuông có đáp án

Trắc nghiệm Bài Ôn tập Chương 3 có đáp án

1 2,039 16/02/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3