SBT Toán 8 Bài 2: Diện tích hình chữ nhật

Mục lục Giải SBT Toán 8 Bài 2: Diện tích hình chữ nhật

Bài 12 trang 157 SBT Toán 8 Tập 1: Diện tích hình chữ nhật thay đổi như thế nào:

a) Chiều dài tăng 3 lần, chiều rộng không thay đổi?

b) Chiều rộng giảm 2 lần, chiều dài không thay đổi?

c) Chiều dài và chiều rộng đều tăng 4 lần?

d) Chiều dài tăng 4 lần, chiều rộng giảm 3 lần?

Lời giải:

Theo công thức tính diện tích hình chữ nhật S = ab thì diện tích của hình chữ nhật tỉ lệ thuận với chiều dài và chiều rộng của hình chữ nhật đó.

Gọi chiều dài của hình chữ nhật là a, chiều rộng là b, diện tích là S,

chiều dài mới a', chiều rộng mới b', diện tích mới S'.

a) Nếu a' = 3a, b' = b

⇒ S' = a'.b' = 3ab = 3S. Diện tích hình mới bằng 3 lần diện tích hình đã cho.

b) Nếu b' = $\frac{1}{2}$b, a' = a

⇒ S' =a'.b' = a. $\frac{1}{2}b=\frac{1}{2}ab=\frac{1}{2}S$.

Diện tích hình mới bằng một nửa diện tích hình đã cho.

c) Nếu a' = 4a, b' = 4b

⇒ S' = a'.b' = 4a.4b = 16ab = 16S.

Diện tích hình mới bằng 16 lần diện tích hình đã cho.

d) Nếu a' = 4a, b' = $\frac{1}{3}$b

⇒ S' = a'.b' = 4a. $\frac{1}{3}b=\frac{4}{3}ab=\frac{4}{3}\text{\hspace{0.17em}}S$.

Diện tích hình mới bằng $\frac{1}{3}$ diện tích hình đã cho.

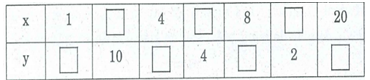
Bài 13 trang 157 SBT Toán 8 Tập 1: Cho hình chữ nhật có diện tích 20 (đơn vị diện tích) và hai kích thước x và y (đơn vị dài).

a) Hãy điền vào ô trống trong bảng sau.

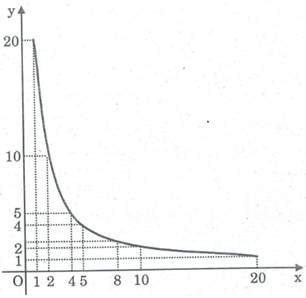
b) Theo bảng vừa thành lập, hãy biểu diễn bảy điểm của đồ thị hàm số trên mặt phẳng tọa độ xOy.

Lời giải:

a) Vì hình chữ nhật có diện tích là 20 nên ta luôn có: xy = 20.

Từ đó, ta có bảng sau:

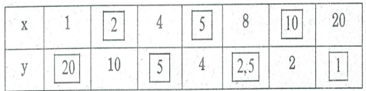
b) Vẽ hình

Bài 14 trang 157 SBT Toán 8 Tập 1:

a) Diện tích hình chữ nhật tăng bao nhiêu phần trăm nếu mỗi cạnh tăng 10%.

b) Diện tích hình chữ nhật giảm bao nhiêu phần trăm nếu mỗi cạnh giảm 10%.

Lời giải:

a) Gọi chiều dài, chiều rộng của hình chữ nhật là a và b ( a > b > 0).

Nếu mỗi cạnh tăng 10% thì độ dài mỗi cạnh sau khi tăng là:

$\begin{array}{l}a+\text{\hspace{0.17em}}10\%a=\frac{110}{100}a;\\ b+\text{}10\%b=\frac{110}{100}b\end{array}$  

Diện tích hình chữ nhật mới là: 

$\frac{110}{100}a.\frac{110}{100}b$

Phần diện tích tăng thêm là: 

$\begin{array}{l}\frac{110}{100}a.\frac{110}{100}b-ab\\ =\frac{121}{100}ab-ab\\ =\frac{21}{100}ab\end{array}$

Vậy diện tích tăng thêm 21% so với diện tích ban đầu.

b) Nếu mỗi cạnh giảm đi 10% thì độ dài mỗi cạnh sau khi giảm 

Diện tích hình chữ nhật mới là: 

$\begin{array}{l}a-10\%a=\frac{90}{100}a;\\ b-10\%b=\frac{90}{100}b\end{array}$

Phần diện tích bị giảm đi là:

 $\begin{array}{l}ab-\frac{90}{100}a.\frac{90}{100}b\\ =ab-\frac{81}{100}ab\\ =\frac{19}{100}ab\end{array}$

Vậy diện tích của hình giảm đi 19% so với diện tích hình ban đầu.

Bài 15 trang 157 SBT Toán 8 Tập 1: Diện tích của một hình chữ nhật bằng 48 cm², một cạnh của nó có độ dài 8cm. Đường thẳng song song với một trong các cạnh của hình chữ nhật chia hình chữ nhật đó thành hai hình chữ nhật bằng nhau. Tính chu vi của mỗi hình chữ nhật được tạo thành.

Lời giải:

Diện tích hình chữ nhật 48 cm², một cạnh có độ dài bằng 8 cm thì độ dài cạnh kia là: 48 : 8 = 6 (cm)

TH1: Chia hình chữ nhật bởi trung điểm của chiều dài thì ta có hai hình chữ nhật bằng nhau có kích thước là 4 cm và 6cm.

Chu vi mỗi hình là: (4 + 6). 2 = 20 (cm)

TH2: Chia hình chữ nhật bởi trung điểm của chiều rộng thì ta có hai hình chữ nhật bằng nhau có kích thước là 8 cm và 3 cm.

Chu vi mỗi hình là: (8 + 3).2 = 22 (cm)

Bài 16 trang 157 SBT Toán 8 Tập 1: Tính các cạnh của một hình chữ nhật, biết bình phương của độ dài một cạnh bằng 16 và diện tích của hình chữ nhật bằng 28cm².

Lời giải:

Gọi độ dài hai cạnh của hình chữ nhật là a và b (a > 0, b > 0)

Theo bài ra, giả sử ta có: a² = 16 và ab = 28

Vì a² = 16 ⇒ a = 4 (cm) (vì a > 0)

Mà ab = 28 ⇒ b = 28 : a = 28 : 4 = 7 (cm)

Vậy hai kích thước là 4cm và 7cm.

Bài 17 trang 157 SBT Toán 8 Tập 1: Tính các cạnh của một hình chữ nhật, biết tỉ số các cạnh là $\frac{4}{9}$ và diện tích của nó là 144 cm².

Lời giải:

Gọi độ dài hai cạnh hình chữ nhật là a và b (0 < a < b).

Theo bài ta, ta có: $\frac{a}{b}=\frac{4}{9}$ và ab = 144

Vì $\frac{a}{b}=\frac{4}{9}$ nên $a=\frac{4}{9}b$

Mà ab = 144 suy ra: $\frac{4}{9}$b.b = 144

$$\begin{gathered} \Rightarrow b^2=144:\frac{4}{9} \\ =144.\frac{9}{4} \\ =324={18}^2 \end{gathered}$$

⇒ b = 18 (cm)

⇒ a = $\frac{4}{9}$. 18 = 8 (cm).

Vậy độ dài các cạnh của hình chữ nhật là 18 cm và 8 cm.

Bài 18 trang 158 SBT Toán 8 Tập 1: Cho tam giác vuông cân, biết độ dài cạnh huyền là l. Tính diện tích tam giác đó.

Lời giải:

Gọi độ dài cạnh góc vuông của tam giác vuông cân là a (0 < a < l)

Áp dụng định lí Pi-ta-go vào tam giác vuông ta có:

$$\begin{gathered} a^2\text{}+\text{\hspace{0.17em}}{a}^2=l^2 \\ \Rightarrow 2a^2=l^2 \end{gathered}$$

$\Rightarrow a^2=\frac{l^2}{2}$

Diện tích tam giác vuông đó là:

$$\begin{gathered} S=\frac{1}{2}{a}^2 \\ =\frac{1}{2}.\frac{l^2}{2} \\ =\frac{l^2}{4} \end{gathered}$$

Bài 19 trang 158 SBT Toán 8 Tập 1: Tính diện tích các hình trong hình vẽ sau (mỗi ô vuông là một đơn vị diện tích). Hãy giải thích vì sao tính được như vậy.

Lời giải:

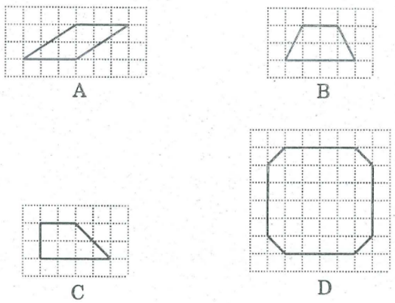
+ Hình A cắt rời thành hai tam giác ghép lại được một hình chữ nhật có một cạnh 3 ô vuông và một cạnh 2 ô vuông nên có diện tích là :

 3.2 = 6 ô vuông (6 đơn vị diện tích).

+ Hình B là một hình thang cân, cắt theo đường cao kẻ từ một đỉnh của đáy nhỏ ghép lại ta được một hình chữ nhật có một cạnh 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng 3.2 = 6 ô vuông (6 đơn vị diện tích).

+ Hình C là hình thang vuông, cắt phần nhọn ghép lên phần trên, ta được một hình chữ nhật có một cạnh là 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng

3.2 = 6 ô vuông (6 đơn vị diện tích).

+ Hình D ta lấy diện tích hình vuông có cạnh 5 ô vuông trừ đi phần khuyết của 4 góc mỗi góc là một nửa ô vuông ta có diện tích là :

$5.5-4.\frac{1}{2}=23$ ô vuông (23 đơn vị diện tích).

Bài 20 trang 158 SBT Toán 8 Tập 1: Trên giấy ô vuông hãy vẽ:

a) Hai hình chữ nhật có cùng chu vi khác diện tích.

b) Hai hình chữ nhật có kích thước khác nhau nhưng có diện tích bằng nhau.

Lời giải:

* Hình a:

Chu vi mỗi hình là 10 (đơn vị)

Diện tích hai hình lần lượt là: 3.2 = 6 và 4.1 = 4 (đơn vị diện tích).

* Hình b:

Chu vi mỗi hình lần lượt là: (6 + 1).2 = 14 và (3 + 2).2 = 10 (đơn vị).

Diện tích hai hình bằng nhau và bằng: 6.1 = 3.2 = 6 (đơn vị diện tích).

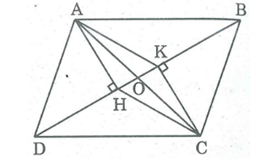
Bài 21 trang 158 SBT Toán 8 Tập 1: Cho hình bình hành ABCD (như hình vẽ). Từ A và C kẻ AH và CK vuông góc với đường chéo BD. Chứng minh rằng hai đa giác ABCH và ADCK có cùng diện tích.

Lời giải:

Ta có:

ΔABC = ΔCDA (c.c.c)

⇒ S_ABC = S_ADC (1)

ΔAHC = ΔCKA (c.c.c)

⇒ S_AHC = S_AKC (2)

Từ (l) và (2) ⇒ S_ABC + S_AHC = S_ADC + S_AKC

Hay S_ABCH = S_ADCK 

Bài 22 trang 158 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E, F.

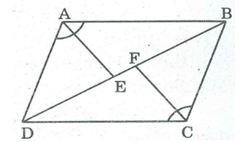
a) Chứng minh hai hình ABCFE và ADCFE có cùng diện tích.

b) Các hình đó có phải là đa giác lồi không? Vì sao?

Lời giải:

a) Ta có:

ΔABE = ΔCDF (g.c.g)

⇒ S_ABE = S_CDF (l)

ΔAED = ΔCFB (g.c.g)

⇒ S_AED = S_CFB (2)

Từ (1) và (2)

⇒ S_ABE + S_CFB = S_CDF + S_AED

Hay S_ABCFE = S_ADCFE

b) Các hình ABCFE, ADCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.

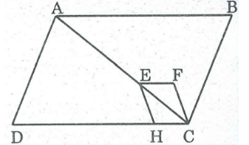
Bài 23 trang 158 SBT Toán 8 Tập 1: Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC.

a) Chứng minh rằng đa giác AEHD và hình ABCFE có diện tích bằng nhau.

b) ABCFE có phải là đa giác lồi không? Vì sao?

Lời giải:

a) Ta có:

ΔABC = ΔCDA (c.c.c)

⇒ S_ABC = S_CDA (1)

ΔEFC = ΔCHE (c.c.c)

⇒ S_EFC = S_CHE (2)

Từ (1) và (2)

⇒ S_ABC – S_EFC = S_CDA – S_CHE

Hay S_ABCFE = S_AEHD

b) Hình ABCFE không phải là tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.

Bài 24 trang 159 SBT Toán 8 Tập 1: Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền (không dùng định lý Py – ta – go).

Lời giải:

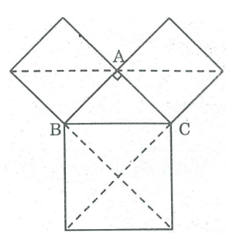
Gọi S là diện tích của tam giác ABC.

Hình vuông có cạnh AB được chia thành hai tam giác vuông cân bằng ΔABC nên diện tích hình vuông cạnh AB bằng 2S.

Hình vuông có cạnh AC được chia thành hai tam giác vuông cân bằng ΔABC nên diện tích hình vuông cạnh AC bằng 2S.

Hình vuông cạnh BC được chia thành bốn hình tam giác vuông cân bằng ΔABC nên có diện tích bằng 4S.

Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên cạnh huyền bằng tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông.

Bài tập bổ sung

Bài 2.1 trang 159 SBT Toán 8 Tập 1: a) Nền của một phòng học có dạng hình chữ nhật, với chiều rộng đo được là 4m và chiều dài là 6m...

Bài 2.2 trang 159 SBT Toán 8 Tập 1: a) Dùng diện tích để chứng tỏ : (a + b)² = a² + 2ab + b²...

Bài 2.3 trang 159 SBT Toán 8 Tập 1: Đố vui a) Có thể dùng kéo cắt một lần và chỉ cắt theo đường thẳng...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 3: Diện tích tam giác

Bài 4: Diện tích hình thang

Bài 5: Diện tích hình thoi

Bài 6: Diện tích đa giác

Ôn tập chương 2 - Phần Hình học

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Diện tích hình chữ nhật có đáp án