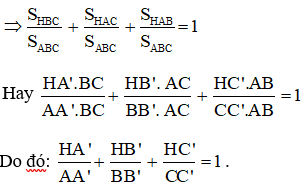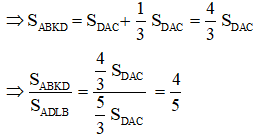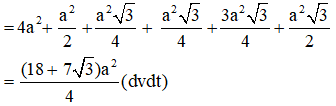Nội dung bài viết

    Xem thêm

    SBT Toán 8 Ôn tập chương 2 - Phần Hình học

    Với giải sách bài tập Toán lớp 8 Bài: Ôn tập chương 2 - Phần Hình học chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 983 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Ôn tập chương 2 - Phần Hình học

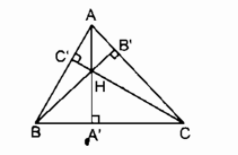
    Bài 51 trang 166 SBT Toán 8 Tập 1: Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chứng minh rằng HA'A​A' +  HB'BB'​  ​+  HC'C​​C'  =1​

    Lời giải:

    Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó (ảnh 1)

    Ta có:

    SHBC= 12HA'.BC;  SHAC  =  12HB'.AC;  SHAB=  12HC'.AB;  SABC= 12AA'.BC= 12BB'.AC=  12CC'.AB

    Và  SHBC + SHAC + SHAB = SABC

    Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó (ảnh 1)

    Bài 52 trang 166 SBT Toán 8 Tập 1: Cho tam giác ABC.

    a) Tính tỉ số đường cao BB’, CC’ xuất phát từ đỉnh B, C.

    b) Tại sao nếu AB < AC thì BB' < CC’?

    Lời giải:

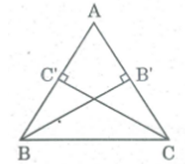
    Cho tam giác ABC. Tính tỉ số đường cao BB’, CC’ xuất phát từ đỉnh B, C (ảnh 1)

    a) Ta có: 

    SABC  =  12BB'.AC =  12CC'.  AB

    Suy ra: BB'.AC = CC'.AB

    Do đó, BB'CC'  =  ABAC.

    b) Nếu AB < AC thì ABAC  <​ 1

    Mà theo a) BB'CC'  =  ABAC

    Suy ra: BB'CC'  <  1

    Do đó, BB' < CC'.

    Bài 53 trang 166 SBT Toán 8 Tập 1: Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thẳng l cắt cạnh AB và CD lần lượt tại M và N. Biết MN = b. Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo).

    Lời giải:

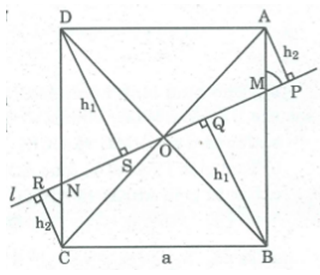
    Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thẳng l cắt cạnh AB và CD (ảnh 1)

    Gọi h1 và h2 là khoảng cách từ đỉnh B và đỉnh A đến đường thẳng l

    Tổng khoảng cách là S.

    Vì O là tâm đối xứng của hình vuông nên OM = ON (tính chất đối xứng tâm)

    MN = b nên MO = NO = b2

    Suy ra AM = CN.

    Mà: AMP^  =  DNS^ (đồng vị)

    Và  (đối đỉnh)

    Suy ra: DNS^  =  C​NR^

    Suy ra: ΔAPM = ΔCRN (cạnh huyền, góc nhọn)

    ⇒ CR = AP = h2

    Vì AM = CN ⇒ BM = DN

    Và  BMQ^  =  DNS^ (so le trong)

    Suy ra: ΔBQM = ΔDSN (cạnh huyền, góc nhọn)

    ⇒ DS = BQ = h1

    SBOA = 14SABCD = 14a2 (l)

    SBOA = SBOM + SAOM 

    =12. b2.h1​​+​  12.b2.h2=  bh1+​  bh24=14.h1+h2b    (2)

    Từ (1) và (2) suy ra

    h1 + h2 = a2b

    Vậy: S = 2(h1 + h2) = 2a2b

    Bài 54 trang 166 SBT Toán 8 Tập 1: Tam giác ABC có hai trung tuyến AM, BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN.

    Lời giải:

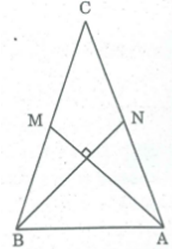
    Tam giác ABC có hai trung tuyến AM, BN vuông góc với nhau (ảnh 1)

    Tứ giác ABMN có hai đường chéo vuông góc nên

    SABMN = 12AM.BN

    Vì Δ ABM và Δ AMC có chung chiều cao kẻ từ A, cạnh đáy BM = MC nên:

    SABM = SAMC = 12SABC

    Vì ΔMNA và ΔMNC có chung chiều cao kẻ từ M, cạnh đáy AN = NC nên:

    SMAN = SMNC = 12SAMC = 14SABC

    Ta có: SABMN = SABM + SMNA 

    = 12SABC + 14SABC = 34SABC

    Vậy SABC = 43SABMN

    = 43.12.AM.BN

    = 23AM.BN.

    Bài 55 trang 166 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc BC sao cho BK = KL = LC. Tính tỉ số diện tích của:

    a) Các tam giác DAC và DCK;

    b) Tam giác DAC và tứ giác ADLB;

    c) Các tứ giác ABKD và ABLD.

    Lời giải:

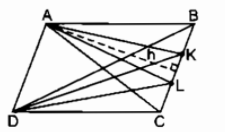
    Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc BC sao cho BK = KL = LC (ảnh 1)

    a) Ta có: SACD = SBCD = SDAB 

    = SCAB = 12SABCD (1)

    ΔDCK và ΔDCB có chung chiều cao kẻ từ đỉnh D, cạnh đáy CK = 23CB nên

    SDCK = 23SDBC (2)

    Từ (1) và (2) ⇒ SDCK  = 23SDA​C 

     ⇒SD​C​KSD​A​C  =  23

    b) Ta có: SADLB = SADB + SDLB

    Vì ΔDBC và ΔDLB có chung chiều cao kẻ từ D, cạnh đáy LB = 23BC

    ⇒ SDLB = 23SDBC

    Mà SDAC = SADB = SDBC (chứng minh trên)

    Suy ra:

    SADLB = SDAC + 23SDAC 

    = 53SDAC 

    ⇒  SDA​CSADLB  = 35

    c) Ta có: SABKD = SABD + SDKB

    Vì ΔDKB và ΔDCB có chung chiều cao kẻ từ D, cạnh đáy BK = 13BC

    ⇒ SDKB = 13SDCB

    Mà SDCB = SDAC = SABD (chứng minh trên).

    Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc BC sao cho BK = KL = LC (ảnh 1)

    Bài 56 trang 166 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A và có BC = 2AB = 2a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC.

    a) Tính các góc B, C, cạnh AC và diện tích tam giác ABC.

    b) Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE.

    c) Tính diện tích tứ giác DEFG.

    Lời giải:

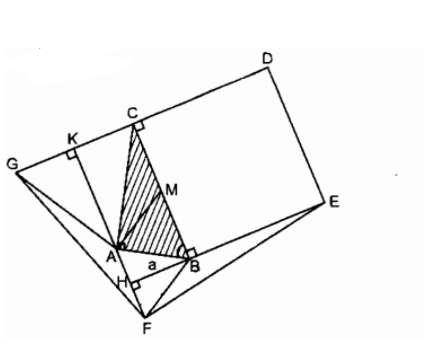
    Cho tam giác ABC vuông tại A và có BC = 2AB = 2a. Ở phía ngoài tam giác (ảnh 1)

    a) Gọi M là trung điểm của BC, ta có:

    AM = MB = BC = a (tính chất trung tuyến của tam giác vuông)

    Suy ra MA = MB = AB = a.

    Suy ra ΔAMB đều

    ⇒ ABC^= 60o

    Mặt khác: ABC^  +  ACB^ = 90° (tính chất tam giác vuông)

    Suy ra: ACB^ = 90o - A​BC^

     = 90o – 60o = 30o

    Trong tam giác vuông ABC, theo Pi-ta-go, ta có:

    BC2 = AB2+ AC2

    ⇒ AC2 = BC2 - AB2 

    = 4a2 - a2 = 3a2 

    ⇒ AC = a3

    Vậy SABC = 12.AB.AC

    =  12a.  a3  =  a232  ( đvdt).

    b) Ta có: FAB^  =  ABC^ = 60o

    Do đó: FA // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

    Và BC ⊥ BE (vì BCDE là hình vuông)

    Suy ra: FA ⊥ BE

    Vì BC ⊥ CD (vì BCDE là hình vuông) và FA // BC

    Suy ra: FA ⊥ CD

    Gọi giao điểm BE và FA là H, FA và CD là K.

    ⇒ BH ⊥ FA và FH = HA = a2 (tính chất tam giác đều)

    Ta có:

    ACG^  ​+  ACB^​​  +​  BCD^

     = 60o + 30o + 90o = 180o

    ⇒ G, C, D thẳng hàng

    ⇒ AK ⊥ CG và GK = KC =12GC  =  12AC  = a32

    SFAG = 12GK.AF

    = 12. a32. a

    =  a234 ( đvdt)

    SFBE = 12FH.BE

    = 12.  a2.2a = 12a2 (đvdt)

    c) SBCDE = BC2 = (2a)2 = 4a2 (dvdt)

    Trong tam giác vuông BHA, theo Pi-ta-go, ta có:

    AH2 + BH2 = AB2

    ⇒ BH2 = AB2 - AH2 

    =a2−  a24  =   3a24 

     ⇒BH = a32

    SABF = 12BH.FA

    =  12.  a32 .a  

     = a234 ( đvdt)

    Trong tam giác vuông AKC, theo Pi-ta-go, ta có:

    AC2 = AK2 + KC2

    ⇒ AK2 = AC2 - KC2 

    =3a2 −  3a24  =  9a24 

    ⇒AK  =  3a2

    SACG = AK.CG

    = 12.  3a2 .a3 

     = 3a234  ( đvdt)

    Ta có:

    SDEFG = SBCDE + SFBE + SFAB + SFAG + SACG + SABC

    Cho tam giác ABC vuông tại A và có BC = 2AB = 2a. Ở phía ngoài tam giác (ảnh 1)

    Bài tập bổ sung

    Bài II.1 trang 166 SBT Toán 8 Tập 1: Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh...

    Bài II.2 trang 166 SBT Toán 8 Tập 1: Cho hình lục giác ABCDEF, có AB = BC = 3cm và ED = 4cm. Biết rằng ED song song với AB, AB...

    Bài II.3 trang 167 SBT Toán 8 Tập 1: Cho lục giác đều MNPQRS (h.bs.27). Gọi X, Y, Z tương ứng là trung điểm của các cạnh MN, PQ và RS...

    Bài II.4 trang 167 SBT Toán 8 Tập 1: Cho tứ giác MNPQ và các kích thước đã cho trên hình bs.28. Diện tích tam giác MQP bằng...

    Bài II.5 trang 167 SBT Toán 8 Tập 1: Cho hình bs.29, trong đó HK = KF = FL = LT và tam giác GHT có diện tích S. Khi đó...

    Bài II.6 trang 167 SBT Toán 8 Tập 1: Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN)...

    Bài II.7 trang 168 SBT Toán 8 Tập 1: Cho hình bs.31, (R là điểm bất kì trên QS, S là điểm bất kì trên NO, hình thang NOPQ có diện tích S)...

    Bài II.8 trang 168 SBT Toán 8 Tập 1: Cho tam giác MNP. Điểm T nằm trong tam giác MNP sao cho các tam giác TMN, TMP, TPN có diện tích bằng nhau...

    Bài II.9 trang 168 SBT Toán 8 Tập 1: Cho hình bs.32 (tam giác MNP vuông tại đỉnh M và NRQP, PUTM, MKHN đều là hình vuông...

    Bài II.10 trang 169 SBT Toán 8 Tập 1: Nếu độ dài cạnh của một hình vuông tăng gấp bốn lần thì diện tích hình vuông đó tăng lên bao nhiêu lần...

    Bài II.11 trang 169 SBT Toán 8 Tập 1: Nếu một hình chữ nhật có chu vi là 16 (cm) và diện tích là 12 (cm2) thì độ dài hai cạnh của nó bằng...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 1: Mở đầu về phương trình

    Bài 2: Phương trình bậc nhất một ẩn và cách giải

    Bài 3: Phương trình đưa về dạng ax + b = 0

    Bài 4: Phương trình tích

    Bài 5: Phương trình chứa ẩn ở mẫu

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Bài Ôn tập Chương 2 có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 983 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: