SBT Toán 8 Bài 11: Hình thoi

Mục lục Giải SBT Toán 8 Bài 11: Hình thoi

Bài 132 trang 96 SBT Toán 8 Tập 1: Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là một hình thoi.

Lời giải:

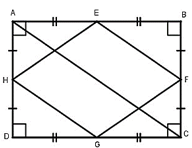
Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA của hình chữ nhật ABCD.

Kẻ đường chéo AC, BD.

* Trong ΔABC, ta có:

E là trung điểm của AB

F là trung điểm của BC

Nên EF là đường trung bình của ΔABC.

⇒ EF // AC và EF = $\frac{1}{2}$AC (tính chất đường trung bình của tam giác) (1)

Trong ΔADC, ta có:

H là trung điểm của AD và G là trung điểm của DC

Nên HG là đường trung bình của tam giác ADC.

⇒ HG // AC và HG = $\frac{1}{2}$AC (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Xét ΔAEH và ΔDGH, ta có:

AH = HD (H là trung điểm của AD)

$\widehat{EAH}=\widehat{GDH}$= 90^o

AE = DG (vì AB = CD)

Suy ra: ΔAEH = ΔDGH (c.g.c)

⇒ HE = HG

Vậy hình bình hành EFGH là hình thoi (hình bình hành có 2 cạnh kề bằng nhau).

Bài 133 trang 96 SBT Toán 8 Tập 1: Chứng minh rằng trung điểm các cạnh của một hình thoi là đỉnh của một hình chữ nhật.

Lời giải:

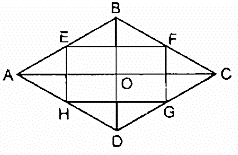
Giả sử hình thoi ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

* Trong ΔABC, ta có:

E là trung điểm của AB và F là trung điểm của BC

Nên EF là đường trung bình của ΔABC.

⇒ EF // AC và EF = $\frac{1}{2}$AC (tính chất đường trung bình của tam giác) (1)

* Trong ΔADC, ta có:

H là trung điểm của AD và G là trung điểm của CD

Nên HG là đường trung bình của tam giác ADC

⇒ HG // AC và HG = $\frac{1}{2}$AC (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra:

EF // HG và EF = HG.

Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Mặt khác: AC ⊥ BD (tính chất hình thoi)

EF // AC (chứng minh trên)

Suy ra: EF ⊥ BD.

Trong ΔABD ta có E là trung điểm của AB; H là trung điểm của AD

  EH là đường trung bình

⇒ EH // BD (tính chất đường trung bình của tam giác)

Suy ra: EH ⊥ EF hay  $\widehat{FEH}$ = 90°

Vậy hình bình hành EFGH là hình chữ nhật.

Bài 134 trang 97 SBT Toán 8 Tập 1: Chứng minh rằng trong hình thoi:

a) Giao điểm của hai đường thẳng chéo là tâm đối xứng của hình thoi.

b) Hai đường chéo là hai trục đối xứng của hình thoi.

Lời giải:

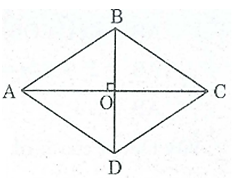
a) Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo. Hình thoi cũng là một hình bình hành nên cũng có tâm đối xứng là giao điểm hai đường chéo của nó.

b)

* Ta có: AC ⊥ BD (tính chất hình thoi)

OB = OD (tính chất hình thoi)

Nên AC là đường trung trực của BD.

Do đó điểm đối xứng với điểm B qua AC là D;

Điểm đối xứng với điểm D qua AC là B

Điểm đối xứng với điểm A qua AC là điểm A;

Điểm đối xứng với điểm C qua AC là điểm C

Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua AC cũng thuộc hình thoi

Do đó AC là trục đối xứng của hình thoi ABCD.

* Ta có : OC = OA và AC ⊥ BD (tính chất hình thoi)

Nên BD là đường trung trực của AC

Do đó điểm đối xứng với điểm A qua BD là điểm C

Điểm đối xứng với điểm C qua BD là điểm A

Điểm đối xứng với điểm B qua BD là điểm B

Điểm đối xứng với điểm D qua BD là điểm D

Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua BD cũng thuộc hình thoi.

Do đó BD là trục đối xứng của hình thoi ABCD.

Bài 135 trang 97 SBT Toán 8 Tập 1: Tứ giác ABCD có tọa độ các đỉnh như sau A(0; 2); B(3; 0); C(0; -2); D(-3; 0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.

Lời giải:

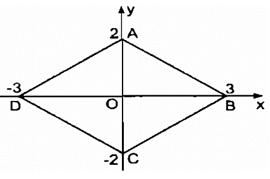
Ta có: A(0; 2) và C(0; -2) là hai điểm đối xứng qua O(0;0)

⇒ OA = OC

B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)

⇒ OB = OD

Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Lại có: Ox ⊥ Oy hay AC ⊥ BD.

Vậy tứ giác ABCD là hình thoi

Trong ΔOAB vuông tại O, theo định lý Py-ta-go ta có:

AB² = OA² + OB²

AB² = 2² + 3² = 4 + 9 = 13

AB = $\sqrt{13}$

Vậy chu vi của hình thoi bằng 4AB = 4$\sqrt{13}$  (đơn vị độ dài)

Bài 136 trang 97 SBT Toán 8 Tập 1:

a) Cho hình thoi ABCD. Kẻ đường cao AH, AK. Chứng minh rằng AH = AK.

b) Hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh rằng ABCD là hình thoi.

Lời giải:

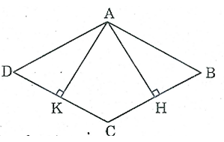
a) Xét hai tam giác vuông AHB và AKD, ta có:

$\widehat{AHB}=\widehat{AKD}$ = 90^o

AB = AD (ABCD là hình thoi)

$\widehat{B}=\widehat{D}$ (tính chất hình thoi)

Suy ra: ΔAHB = ΔAKD (cạnh huyền - góc nhọn)

⇒ AH = AK

b)

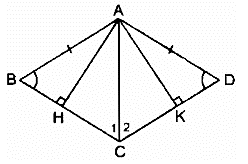
Xét hai tam giác vuông AHC và AKC, ta có:

$\widehat{AHC}=\widehat{AKC}$ = 90^o

AH = AK (giả thiết)

AC cạnh huyền chung

Suy ra: ΔAHC = ΔAKC (cạnh huyền - cạnh góc vuông)

⇒ $\widehat{ACH}=\widehat{ACK}$ hay $\widehat{ACB}=\widehat{ACD}$

⇒ CA là tia phân giác $\widehat{BCD}$

Hình bình hành ABCD có đường chéo CA là đường phân giác nên là hình thoi.

Bài 137 trang 97 SBT Toán 8 Tập 1: Hình thoi ABCD có $\hat{A}$ = 60^o. Kẻ hai đường cao BE, BF. Tam giác BEF là tam giác gì? Vì sao?

Lời giải:

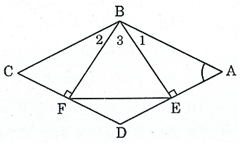
Xét hai tam giác vuông BEA và BFC, ta có:

$\widehat{BEA}=\widehat{BFC}$ = 90^o

$\widehat{A}=\widehat{C}$ (tính chất hình thoi)

BA = BC (giả thiết)

Suy ra: ΔBEA = ΔBFC (cạnh huyền - góc nhọn)

Do đó, ta có:

* BE = BF ⇒ ΔBEF cân tại B

* $\widehat{B_1}=\widehat{B_2}$

Trong tam giác vuông BEA, ta có:

$\widehat{A}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{B_1}$ = 90^o 

⇒ $\widehat{B_1}$ = 90^o – $\widehat{A}$  

= 90^o – 60^o = 30^o

⇒ $\widehat{B_1}=\widehat{B_2}$ = 30^o

Lại có: $\widehat{A}+\text{\hspace{0.17em}}\widehat{ABC}$ = 180^o (hai góc trong cùng phía bù nhau)

⇒ $\widehat{ABC}$ = 180^o – $\widehat{A}$

= 180^o – 60^o = 120^o

Ta có: $\widehat{ABC}=\widehat{B_1}+\widehat{B_2}+\text{\hspace{0.17em}}\widehat{B_3}$

⇒ $\widehat{B_3}=\widehat{ABC}-\left(\widehat{B_1}+\widehat{B_2}\right)$

 = 120^o - (30^o + 30^o) = 60^o

Tam giác BEF cân tại B có $\widehat{EBF}$ = 60^o nên ΔBEF đều.

Bài 138 trang 97 SBT Toán 8 Tập 1: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

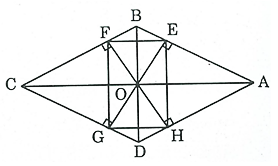
Ta có: AB // CD (do ABCD là hình thoi)

OE ⊥ AB (giả thiết)

⇒ OE ⊥CD

Mà OG ⊥CD (giả thiết)

Suy ra OE trùng với OG nên ba điểm O,E,G thẳng hàng.

Ta có: BC // AD (do ABCD là hình thoi)

Và OF ⊥ BC (giả thiết)

⇒ OF ⊥ AD

Mà OH ⊥ AD (gỉa thiết)

Suy ra OF trùng với OH nên ba điểm O,H,F thẳng hàng.

Vì AC và BD là đường phân giác các góc của hình thoi nên:

OE = OF (tính chất tia phân giác) (1)

OE = OH (tính chất tia phân giác) (2)

OH = OG (tính chất tia phân giác) (3)

Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình chữ nhật.

Bài 139 trang 97 SBT Toán 8 Tập 1: Hình thoi ABCD có chu vi bằng 16cm, đường cao AH = 2cm. Tính các góc của hình thoi, biết .

Lời giải:

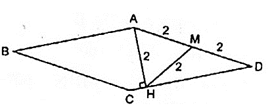
Chu vi hình thoi bằng 16(cm) nên độ dài một cạnh bằng:

16 : 4 = 4(cm).

Gọi M là trung điểm của AD.

*Trong tam giác vuông AHD ta có HM là trung tuyến thuộc cạnh huyền, suy ra:

HM = AM = $\frac{1}{2}$AD

= $\frac{1}{2}$. 4 = 2(cm)

⇒ AM = HM = AH = 2cm

⇒ Δ AHM đều

⇒$\widehat{HAM}$ = 60^o

*Trong tam giác vuông AHD, ta có:

$\widehat{HAD}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{D}$ = 90^o

⇒$\widehat{D}$ = 90^o - $\widehat{HAD}$

= 90^o – 60^o = 30^o

⇒ $\widehat{B}=\widehat{D}$ = 30^o (tính chất hình thoi)

Lại có: $\widehat{B}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{C}$ = 180^o (hai góc trong cùng phía bù nhau)

⇒ $\widehat{C}$ = 180^o - $\widehat{B}$ 

= 180^o – 30^o = 150^o

⇒ $\widehat{A}=\widehat{C}$ = 150^o (tính chất hình thoi).

Bài 140 trang 97 SBT Toán 8 Tập 1: Hình thoi ABCD có góc A = 60°. Trên cạnh AD lấy điểm M, trên cạnh CD lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì? Vì sao?

Lời giải:

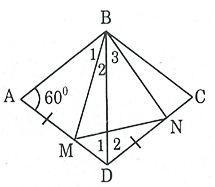
Nối BD, ta có AB = AD (do ABCD là hình thoi)

Suy ra Δ ABD cân tại A

Mà $\widehat{A}$ = 60^o ⇒ ΔABD đều

⇒ $\widehat{ABD}=\widehat{D_1}$ = 60^o và BD = AB.

Suy ra: BD = BC = CD.

⇒ΔCBD đều ⇒ $\widehat{D_2}$ = 60^o

Xét ΔBAM và ΔBDN, ta có:

AB = BD (chứng minh trên)

$\widehat{A}=\widehat{D_2}$ = 60^o

AM = DN (giả thiết)

Do đó ΔBAM = ΔBDN (c.g.c) .

⇒ $\widehat{B_1}=\widehat{B_3}$ và BM = BN.

Suy ra ΔBMN cân tại B.

Mà $\widehat{B_2}+\widehat{B_1}=\widehat{ABD}$ = 60^o

Suy ra:

$\widehat{B_2}+\widehat{B_3}$ $=\widehat{B_2}+\widehat{B_1}$ = 60° hay $\widehat{MBN}$ = 60^o

Vậy ΔBMN đều.

Bài 141 trang 97 SBT Toán 8 Tập 1: Cho tam giác ABC. Lấy các điểm D,E theo thứ tự trên cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K theo thứ tự là trung điểm của BE, CD, DE, BC. Chứng minh rằng IK vuông góc với MN.

Lời giải:

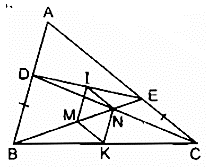
*Trong ΔBCD,ta có:

K là trung điểm của BC (giả thiết)

N là trung điểm của CD (giả thiết)

Nên NK là đường trung bình của ΔBCD

⇒ NK // BD và NK = $\frac{1}{2}$BD (tính chất đường trung bình trong tam giác) (1)

*Trong ΔBED,ta có:

M là trung điểm của BE (giả thiết)

I là trung điểm của DE (giả thiết)

Nên MI là đường trung bình của ΔBED

⇒ MI // BD và MI = $\frac{1}{2}$BD (tính chất đường trung bình trong tam giác) (2)

Từ (1) và (2) suy ra:

MI // NK và MI = NK.

Nên tứ giác MKNI là hình bình hành.

*Trong ΔBEC ta có

M là trung điểm của BE; K là trung điểm của BC nên MK là đường trung bình của tam giác BEC

⇒ MK = CE (tính chất đường trung bình của tam giác)

BD = $\frac{1}{2}$CE (giả thiết).

Suy ra: MK = KN

Vậy hình bình hành MKNI là hình thoi (hình bình hành có hai cạnh kề bằng nhau là hình thoi)

⇒IK ⊥ MN (tính chất hình thoi).

Bài 142 trang 97 SBT Toán 8 Tập 1: Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E, F, G, H theo thứ tự là giao điểm của các đường phân giác của tam giác AOB, BOC, COD, DOA. Chứng minh rằng EFGH là hình thoi.

Lời giải:

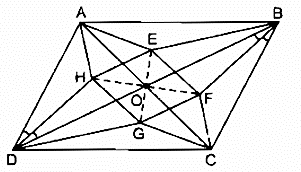
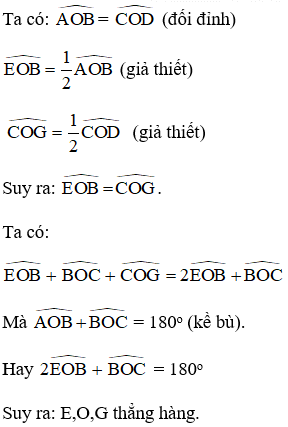
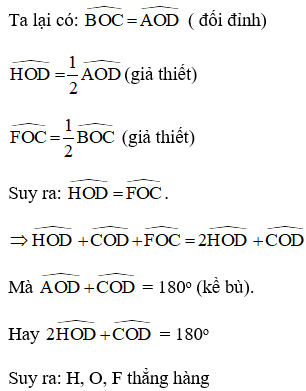
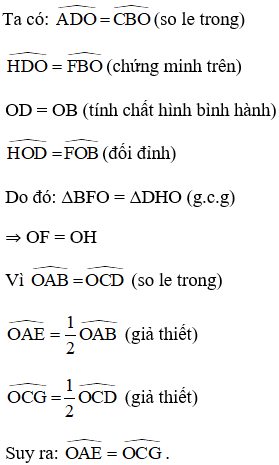
Xét ΔOAE và ΔOCG,ta có :

$\widehat{OAE}=\widehat{OCG}$ (chứng mình trên)

OA = OC (tính chất hình bình hành)

$\widehat{EOA}=\widehat{GOC}$ (đối đỉnh)

Do đó: ΔOAE= ΔOCG (g.c.g)

⇒ OE = OG

Suy ra tứ giác EFGH là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

OE ⊥ OF (tính chất tia phân giác của hai góc kề bù) hay EG ⊥ FH

Vậy tứ giác EFGH là hình thoi.

Bài 143 trang 97 SBT Toán 8 Tập 1: Dựng hình thoi ABCD biết cạnh bằng 2cm, một đường chéo bằng 3cm.

Lời giải:

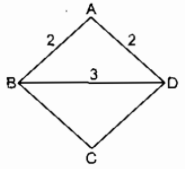
*Cách dựng:

- Dựng ΔABD biết AB = AD = 2(cm), BD = 3(cm).

- Trên nửa mặt phẳng bờ BD không chứa điểm A. Từ B dựng tia Bx // AD, từ D dựng tia Dy // AB, chúng cắt nhau tại C.

Ta có hình thoi ABCD cần dựng.

*Chứng minh:

Vì AB // CD và AD // BC nên tứ giác ABCD là hình bình hành

AB = AD = 2cm. Vậy tứ giác ABCD là hình thoi.

Lại có: BD = 3cm

Hình thoi dựng được thỏa mãn điều kiện bài toán.

Bài tập bổ sung

Bài 11.1 trang 97 SBT Toán 8 Tập 1: Cạnh của một hình thoi bằng 25, một đường chéo bằng 14. Đường chéo kia bằng...

Bài 11.2 trang 97 SBT Toán 8 Tập 1: Cho hình thang cân ABCD (AB // CD). Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA...

Bài 11.3 trang 98 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ đường thẳng song song với AC, cắt AB ở I...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 12: Hình vuông

Ôn tập chương 1 - Phần Hình học

Bài 1: Đa giác - Đa giác đều

Bài 2: Diện tích hình chữ nhật

Bài 3: Diện tích tam giác

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Hình thoi có đáp án