SBT Toán 8 Bài 9: Thể tích của hình chóp đều

Mục lục Giải SBT Toán 8 Bài 9: Thể tích của hình chóp đều

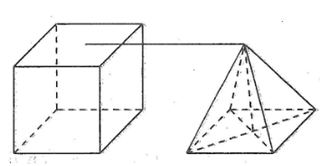
Bài 62 trang 150 SBT Toán 8 Tập 2: Một hình chóp tứ giác đều và một lăng trụ đứng tứ giác đều như hình vẽ (cạnh đáy và chiều cao bằng nhau).

Nếu thể tích hình trụ là V thì thể tích hình chóp là:

A.V;

B. $\frac{V}{2}$;

C. $\frac{V}{3}$.

D. $\frac{V}{4}.$

Hãy chọn kết quả đúng.

Lời giải:

Một hình chóp tứ giác đều và một lăng trụ đứng là tứ giác đều có chiều cao bằng nhau và có diện tích đáy bằng nhau.

Thể tích hình lăng trụ đứng là: V= S. h

Thể tích hình chóp tứ giác đều là

$V\text{'}=\frac{1}{3}S.h=\frac{1}{3}\text{}V$

Vậy nếu thể tích của hình lăng trụ là V thì thể tích là hình chóp là $\frac{V}{3}$.

Vậy chọn đáp án C.

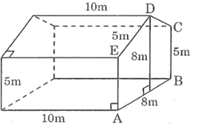
Bài 63 trang 151 SBT Toán 8 Tập 2: Một cái nhà trồng cây thí nghiệm có dạng hình lăng trụ đứng có các kích thước như hình vẽ trong đó EDC là tam giác cân. Hãy tính :

a) Diện tích hình ABCDE;

b) Tính thể tích nhà kính;

c) Diện tích kính cần phải có để “lợp” hai mái và bốn bức tường nhà.

Lời giải:

a) Chia hình ABCDE thành hai hình thang vuông có cạnh đáy nhỏ là 5m đáy lớn 8m, chiều cao là 4m.

Ta có: S_ABCDE = $2.\left(\frac{5+\text{}8}{2}.4\right)=52\left(m^2\right)$.

b) Thể tích hình lăng trụ đứng (nhà kính) là:

V = S.h = 52.10 = 520 (m³)

c) Diện tích nhà kính gồm bốn hình chữ nhật có kích thước là 5m và 10m và hai hình bằng diện tích hình ABCDE.

Diện tích bốn hình chữ nhật là:

(5.10).4 = 200(m²)

Tống diện tích kính cần dùng là:

200 + 52.2 = 304 (m²)

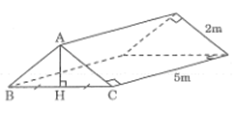
Bài 64 trang 151 SBT Toán 8 Tập 2: Hình vẽ là chiếc lều ở một trại hè với các kích thước trên hình ABC là tam giác vuông cân.

a) Tính thể tích lều.

b) Số vải bạt cần có để dựng lều đó là bao nhiêu? (Không tính các mép gấp đường viền,…)

Lời giải:

a) Lều là lăng trụ đứng đáy tam giác vuông cân, cạnh 2m, chiều cao lăng trụ 5m.

Diện tích đáy là: S_đáy = $\frac{1}{2}$.2.2 = 2 (m²)

Thể tích lều là: V= S.h = 2.5 = 10 (m³)

c) Số vải cần để làm lều là hai mặt bên và hai đầu (hai đáy của lăng trụ đứng)

Diện tích hai mặt bên (hình chữ nhật) là:

(2.5).2 = 20 (m²)

Diện tích vải cần dùng là:

20 + 2.2 = 24 (m²).

Bài 65 trang 151 SBT Toán 8 Tập 2: Xét các hình sau:

1. Kim tự tháp Kê-ốp là một hình chóp tứ giác đều, cạnh đáy bằng 233m, chiều cao hình chóp 146,5m.

a) Độ dài cạnh bên là bao nhiêu?

b) Tính diện tích xung quanh của hình chóp.

c) Tính thể tích hình chóp.

2. Kim tự tháp Lu-vrơ: Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-Vrơ. Mô hình có dạng hình chóp đều cao 21m, độ dài cạnh đáy là 34m.

a) Cạnh bên hình chóp là bao nhiêu?

b) Tính thể tích hình chóp.

c) Tính tổng diện tích các tấm kính để phủ lên hình chóp này.

Lời giải:

Giả sử các kim tự tháp là hình chóp tứ giác đều S.ABCD.

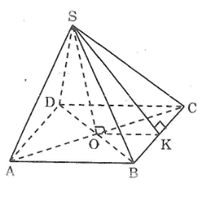
1.

a) Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:

OA² + OB² = AB²

Suy ra: 2. OA² = AB²

Suy ra:

OA² $=\frac{A{B}^2}{2}=\frac{{233}^2}{2}=27144,5$

Áp dụng định lí Pi-ta-go vào tam giác vuông SOA, ta có:

SA² = SO² + OA²

 = (146,5)² + 27144,5 = 48606,75

SA = $\sqrt{48606,75}$ ≈ 220,5 (m)

b) Kẻ SK ⊥ BC

Hình chóp S.ABCD đều nên

SB = SA, AB = BC

Ta có:

BK = KC = $\frac{1}{2}$BC = 116,5(m)

Áp dụng định lí Pi-ta-go vào tam giác vuông SKB, ta có:

SB² = SK² + BK²

Suy ra: SK² = SB² - BK² 

= 48606,75 – 13572,25 = 35034,5

SK = $\sqrt{35034,5}$ (m)

Diện tích xung quanh của kim tự tháp là:

 S = (233.2).$\sqrt{35034,5}$ ≈ 87223,6 (m²)

c) Thể tích hình chóp là :

V= $\frac{1}{3}$.S.h = $\frac{1}{3}$.233.233.146,5

= 2651112,8 (m³)

2. Tương tự câu 1, trong đó tổng diện tích các tấm kính để phủ lên hình chóp chính là diện tích xung quanh của hình chóp.

a) Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:

OA² + OB² = AB²

Suy ra: 2. OA² = AB²

Suy ra:

OA² = $=\frac{A{B}^2}{2}=\frac{{34}^2}{2}=578$

Áp dụng định lí Pi-ta-go vào tam giác vuông SOA, ta có:

SA² = SO² + OA² 

= 21² + 578 = 1019

SA = $\sqrt{1019}$ ≈ 31,9 (m)

b) Thể tích hình chóp là :

V = $\frac{1}{3}$.S.h = $\frac{1}{3}$. 34 . 34 . 21

= 8092 (m³)

c)

 Kẻ SK ⊥ BC

Hình chóp S.ABCD đều nên

SB = SA, AB = BC

Ta có: BK = KC = $\frac{1}{2}$BC = 17 (m)

Áp dụng định lí Pi-ta-go vào tam giác vuông SKB, ta có:

SB² = SK² + BK²

Suy ra:

SK² = SB² - BK² = 1019 – 17² = 730

SK = $\sqrt{730}$ (m)

Diện tích xung quanh của kim tự tháp là:

 S = (34 . 2).$\sqrt{730}$ ≈ 1837,3 (m²)

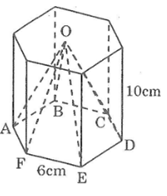
Bài 66 trang 152 SBT Toán 8 Tập 2: Thể tích hình chóp đều cho theo các kích thước ở hình là:

A. 54$\sqrt{3}$ (cm³);

B. 540$\sqrt{3}$ (cm³);

C. 180$\sqrt{3}$ (cm³);

D. 108$\sqrt{3}$ (cm³).

Hãy chọn kết quả đúng

Lời giải:

Hình chóp trong hình có đáy là lục giác đều. Chia lục giác đều thành 6 phần bằng nhau ta được 6 tam giác đều cạnh 6cm.

Diện tích mỗi tam giác đều bằng 

$\frac{6^2\sqrt{3}}{4}=9\sqrt{3}$  (cm²).

Diện tích lục giác đều là:

 $6.9\sqrt{3}=54\sqrt{3}\left(c{m}^2\right)$

Thể tích hình chóp bằng:

$\frac{1}{3}.54\sqrt{3}.10=180\sqrt{3}$(cm³).

Vậy chọn đáp án C.

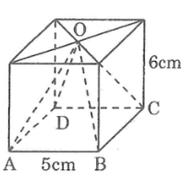
Bài 67 trang 152 SBT Toán 8 Tập 2: Tính thể tích hình chóp tứ giác đều O.ABCD các kích thước cho trên hình

Lời giải:

Hình chóp tứ giác đều đáy là hình vuông.

Diện tích đáy là:

S = 5.5 = 25 (cm²)

Thể tích hình chóp là:

V = $\frac{1}{3}$S.h = $\frac{1}{3}$.25.6 = 50 (cm³).

Bài 68 trang 152 SBT Toán 8 Tập 2: Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao hình chóp là 4cm. Thể tích của hình chóp là:

A. 30 (cm³);

B. 24(cm³);

C. 22(cm³);

D. 18(cm³);

E. 15(cm³).

Hãy chọn kết quả đúng

Lời giải:

Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao 4cm.

Áp dụng định lí Pi-ta-go ta tính được nửa đường chéo của hình vuông đáy là

$\sqrt{5^2-4^2}=3$ (cm)

Suy ra, đường chéo của đáy là 2.3 = 6 (cm).

Diện tích đáy bằng:

$\frac{1}{2}$.6.6 = 18(cm²).

Thể tích của hình chóp là:

V = $\frac{1}{3}$.S.h = $\frac{1}{3}$.18.4 = 24 (cm³).

Vậy chọn đáp án B.

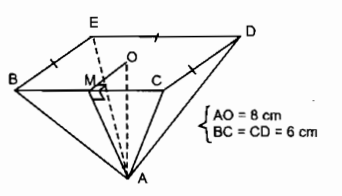
Bài 69 trang 152 SBT Toán 8 Tập 2: Tính diện tích toàn phần của các hình chóp đều sau đây:

a) Hình cho theo các kích thước trên hình sau:

b) Hình chóp tứ giác đều cạnh đáy 6cm, chiều cao hình chóp 5cm;

c) Hình chóp tứ giác đều cạnh đáy 20cm, chiều cao hình chóp 7cm;

d) Hình chóp tứ giác đều cạnh đáy 1m, chiều cao hình chóp 50cm.

Lời giải:

a) Vì AO là đường cao hình chóp nên ΔAOM vuông tại O.

Ta có OM = $\frac{1}{2}$CD = 3 (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:

AM² = AO² + OM² = 8² + 3² = 73

Suy ra: AM = $\sqrt{73}$ (cm)

Ta có:

S_xq = P.d = 6.2.$\sqrt{73}=12\sqrt{73}$  (cm²)

S_đáy = 6.6 = 36 (cm²)

Vậy S_TP = S_xq + S_đáy 

= $12\sqrt{73}$ + 36 ≈ 138,5(cm²)

b) Hình chóp tứ giác đều cạnh đáy bằng 6cm, chiều cao hình chóp bằng 5cm.

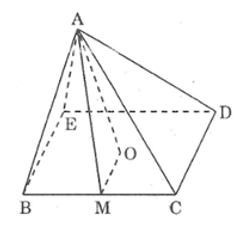
OM = $\frac{CD}{2}$ = 6 : 2 = 3

Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.

Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:

AM² = OA² + OM² = 5² + 3² = 34

Suy ra: AM = $\sqrt{34}$ cm

Ta có:

S_xq = 6.2.$\sqrt{34}=12\sqrt{34}$(cm²)

S_đáy = 6.6 = 36 (cm²)

Vậy S_TP = S_xq + S_đáy 

= $12\sqrt{34}$ + 36 ≈ 106 (cm²)

c) Hình chóp tứ giác đều, cạnh đáy bằng 20cm, chiều cao hình chóp bằng 7cm

MO = 20 : 1 = 10

Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.

Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:

AM² = AO² + MO² 

= 7² + 10² = 149

Suy ra: AM = $\sqrt{149}$ (cm)

Ta có:

S_xq = 20.2.$\sqrt{149}$  = 40$\sqrt{149}$(cm²)

S_đáy = 20.20 = 400 (cm²)

Vậy S_TP = S_xq + S_đáy

= 40$\sqrt{149}$ + 400 ≈ 888,3 (cm²)

d) Hình chóp tứ giác đều, cạnh đáy bằng 1m, chiều cao hình chóp bằng 0,5m.

OM = 1 : 2 = 0,5

Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.

Áp dụng định lí Pi-ta-go vào tam giác vuông AOM,ta có:

AM² =AO² + OM² 

= (0,5)² + (0,5)² = 0,5

Suy ra: AM = $\sqrt{0,5}$ cm

Ta có: S_xq =1.2.$\sqrt{0,5}=2\sqrt{0,5}$  (m²).

S_đáy = 1.1 = 1(m²)

Vậy S_TP = $2\sqrt{0,5}$+ 1 ≈ 2,4 (m²).

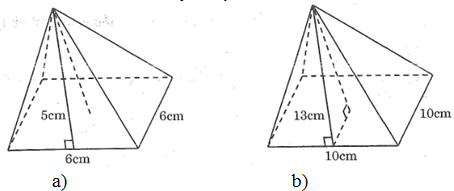
Bài 70 trang 153 SBT Toán 8 Tập 2: Tính thể tích và diện tích toàn phần của hình chóp đều dưới đây theo kích thước cho trên hình

Lời giải:

*Hình a:

Đường cao hình chóp bằng:

$\sqrt{5^2-3^2}=4cm$

Diện tích đáy bằng:

S = 6.6 = 36 (cm²)

Thể tích hình chóp bằng :

V = $\frac{1}{3}$S.h = $\frac{1}{3}$.36.4 = 48 (cm³)

Diện tích xung quanh bằng:

S_xq = Pd = 2.6.5 = 60 (cm²)

Diện tích toàn phần là :

S_TP = S_xq + S_đáy = 60 + 36 = 96 (cm²)

*Hình b:

Đường cao hình chóp bằng: $\sqrt{{13}^2-5^2}=12$cm

Diện tích đáy bằng:

S = 10.10 = 100 (cm²)

Thể tích hình chóp bằng :

V= $\frac{1}{3}$S.h = $\frac{1}{3}$100.12 = 400 (cm³)

Diện tích xung quanh bằng hình chóp bằng :

S_xq = Pd = 10.2.13 = 260 (cm²)

Diện tích toàn phần của hình chóp là:

S_TP = S_xq + S_đáy =260 +100 = 360 (cm²)

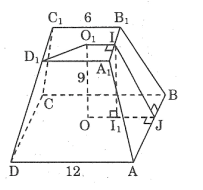
Bài 71 trang 153 SBT Toán 8 Tập 2: Tính diện tích toàn phần của hình chóp cụt đều theo các kích thước cho trên hình

Lời giải:

Ta có: A₁D₁ = 6 ⇒ O₁I = 3

AD = 12 ⇒ OJ = 6

Kẻ II₁ ⊥ OJ ta có: I₁O = 3

Suy ra

I₁I = OJ – I₁O = 6 – 3 = 3;

II₁ = OO₁ = 9

Áp dụng định lí Pi-ta-go vào tam giác vuông II₁J, ta có:

IJ² = II₁² + I₁J² = 9² + 3² = 90

Suy ra: IJ = $\sqrt{90}$.

Diện tích mặt một bên là một hình thang bằng:

 $S=\frac{1}{2}.(6+\text{}12).\sqrt{90}=9\sqrt{90}$(đvdt)

Diện tích xung quanh bằng:

S_xq = $\mathrm{4.9.}\sqrt{90}=36\sqrt{90}$ (đvdt)

Diện tích đáy trên bằng:

S = 6.6 = 36 (đvdt)

Diện tích đáy dưới bằng :

S = 12.12 = 144 (đvdt)

Diện tích toàn phần của hình chóp cụt bằng:

$$\begin{gathered} S_{tp}=36\sqrt{90}+36+144 \\ =36\sqrt{90}+\text{\hspace{0.17em}\hspace{0.17em}}180 \left(đvdt\right) \end{gathered}$$

Bài 72 trang 153 SBT Toán 8 Tập 2: Cho hình chóp cụt tứ giác đều ABCD.A₁B₁C₁D₁ có các cạnh đáy 5cm và 10cm, đường cao của mặt bên bằng 5cm. Hãy tính:

a) Diện tích xung quanh của hình chóp cụt.

b) Tính cạnh bên và đường cao hình chóp cụt.

Lời giải:

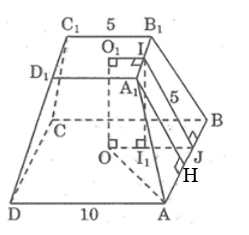
a) Diện tích một mặt bên là hình thang bằng:

S = $\frac{1}{2}$(5 + 10).5 = 37,5 (cm²)

Diện tích xung quanh của hình chóp cụt đều là:

 S_xq = 4 . 37,5 = 150 (cm²)

b) Kẻ A₁H ⊥ AB, ta có:

A₁I = 2,5cm; AJ = 5cm

Suy ra: AH = 5 - 2,5 = 2,5cm

Áp dụng định lí Pi-ta-go vào tam giác vuông A₁HA, ta có:

A₁A² = A₁H² + AH² 

= 5² + 2,5² = 31,25 (A₁H = IJ = 5cm)

Suy ra cạnh bên:

A₁A = $\sqrt{31,25}$ ≈ 5,59 (cm)

Ta có: O₁I = 2,5; OJ = 5cm.

Kẻ II₁ ⊥ OJ, suy ra I₁J = 2,5.

Áp dụng định kí Pi-ta-go vào tam giác vuông II₁J, ta có:

IJ² = II₁² + I₁J²

Suy ra: II₁² = IJ² – I₁J² 

= 5² – 2,5² = 18,75

Suy ra: II₁ = $\sqrt{18,75}$ ≈ 4,33 (cm)

Vậy chiều cao O₁O = II₁ = 4,33 (cm)

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 5: Diện tích xung quanh của hình lăng trụ đứng

Bài 6: Thể tích của hình lăng trụ đứng

Bài 7: Hình chóp đều và hình chóp cụt đều

Bài 8: Diện tích xung quanh của hình chóp đều

Ôn tập chương 4 - Phần Hình học

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Lý thuyết Thể tích của hình chóp đều

Trắc nghiệm Thể tích hình chóp đều có đáp án