Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 6: Đối xứng trục

    Với giải sách bài tập Toán lớp 8 Bài 6: Đối xứng trục chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 1,185 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Bài 6: Đối xứng trục

    Bài 60 trang 86 SBT Toán 8 Tập 1: Cho tam giác ABC có A^ = 70o, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC.

    a) Chứng minh rằng AD = AE;

    b) Tính số đo góc DAE^.

    Lời giải:

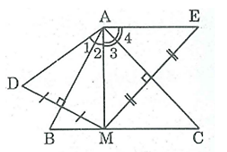
    Cho tam giác ABC có góc A = 70 độ, điểm M thuộc cạnh BC (ảnh 1)

    a) Vì D đối xứng với M qua trục AB

    ⇒ AB là đường trung trực của MD.

    ⇒ AD = AM (t/chất đường trung trực) (1)

    Vì E đối xứng với M qua trục AC

    ⇒ AC là đường trung trực của ME

    ⇒ AM = AE (t/chất đường trung trực) (2)

    Từ (1) và (2) suy ra: AD = AE  (điều phải chứng minh).

    b) Vì AD = AM suy ra ΔAMD cân tại A có AB ⊥ MD nên AB cũng là đường phân giác của MAD^.

    ⇒ A1^  =  A2^

    Vì AM = AE suy ra ΔAME cân tại A có AC ⊥ ME nên AC cũng là đường phân giác của MAE^.

    ⇒ A3^  =  A4^

    Ta có: DAE^= A1^  +  A2^+​ A3^  +  A4^

    = 2 A2^  +  A3^= 2BAC^

    = 2.70o = 140o

    Bài 61 trang 87 SBT Toán 8 Tập 1: Cho tam giác nhọn ABC có A^ = 60o, trực tâm H. Gọi M là điểm đối xứng với H qua BC.

    a) Chứng minh ΔBHC = ΔBMC;

    b) Tính góc BMC^.

    Lời giải:

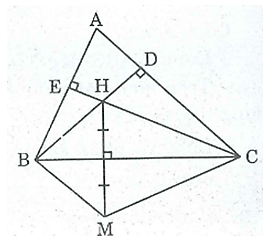
    Cho tam giác nhọn ABC có góc A = 60 độ, trực tâm H (ảnh 1)

    a) Vì M đối xứng với H qua trục BC

    ⇒ BC là đường trung trực của HM

    ⇒ BH = BM (t/chất đường trung trực)

    Và CH = CM (t/chất đường trung trực)

    Xét tam giác BHC và tam giác BMC có:

    BC chung

    BH= BM ( chứng minh trên)

    CH = CM (chứng minh trên)

    Suy ra: ΔBHC = ΔBMC (c.c.c)

    b) Gọi giao điểm BH với AC là D, giao điểm của CH và AB là E, H là trực tâm của ΔABC

    ⇒ BD ⊥ AC, CE ⊥ AB

    Xét tứ giác ADHE, ta có:

    DHE^= 3600  − A^​+​ HDE^ + HED^

     = 360o – ( 60o + 90o + 90o) = 120o

    BHC^ = DHE^(đối đỉnh)   (1)

    Lại có: ΔBHC = ΔBMC (chứng minh trên)

    ⇒ BMC^  = BHC^  (2)

    Từ (1) (2) suy ra:

    BMC^  = DHE^ = 120o

    Bài 62 trang 87 SBT Toán 8 Tập 1: Cho hình thang vuông ABCD ( A^  =  D^ = 90°). Gọi H là điểm đối xứng với B qua AD, I là giao điểm của CH và AD. Chứng minh rằng AIB^  = DIC^.

    Lời giải:

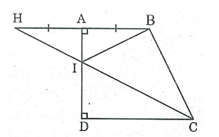
    Cho hình thang vuông ABCD ( góc A = góc D = 90 độ). Gọi H là điểm đối xứng (ảnh 1)

    Tam giác có IHB có IA là đường cao đồng thời là đường trung tuyến nên tam giác IHB cân tại I.

    Suy ra: IA là tia phân giác của góc BI​H^.

    ⇒ AIB^  = AIH^

    Lại có: AIH^  = DIC^ ( 2 góc đối đỉnh)

    Suy ra: AIB^  = DIC^.

    Bài 63 trang 87 SBT Toán 8 Tập 1: Cho hai điểm A, B thuộc cùng một nửa mặt phẳng bờ là đường thẳng xy (AB không vuông góc với xy). Gọi A’ đối xứng với A qua xy, C là giao điểm của A’B và xy. Gọi M là điểm bất kì khác C thuộc đường thẳng xy. Chứng minh rằng: AC + CB < AM + MB.

    Lời giải:

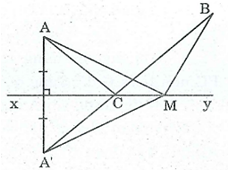
    Cho hai điểm A, B thuộc cùng một nửa mặt phẳng bờ là đường thẳng xy (ảnh 1)

    Vì A' đối xứng với A qua xy

    ⇒ xy là đường trung trực của AA'.

    ⇒ CA' = CA (t/chất đường trung trực)

    MA' = MA (t/chất đường trung trực)

    AC + CB = A'C + CB = A'B (1)

    MA + MB = MA'+ MB (2)

    Trong ΔMA'B, ta có:

    A'B < A'M + MB (bất đẳng thức tam giác) (3)

    Từ (1), (2) và (3) suy ra:

    AC + CB < AM + MB.

    Bài 64 trang 87 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK . Chứng minh rằng điểm I đối xứng với điểm K qua AH.

    Lời giải:

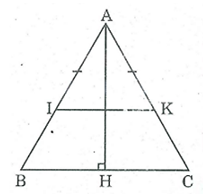
    Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I (ảnh 1)

    Ta có: ΔABC cân tại A; AH ⊥ BC (gt)

    Suy ra: AH là tia phân giác của góc A

    Lại có: AI = AK (gt)

    Suy ra: ΔAIK cân tại A

    Do AH là tia phân giác của góc A

    Nên AH là đường trung trực của IK

    Vậy I đối xứng với K qua AH.

    Bài 65 trang 87 SBT Toán 8 Tập 1: Tứ giác ABCD có AB = BC, AD = DC (hình cái diều). Chứng minh rằng điểm A đối xứng với điểm C qua đường thẳng BD.

    Lời giải:

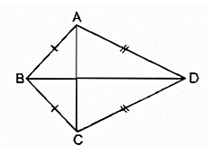
    Tứ giác ABCD có AB = BC, AD = DC (hình cái diều). Chứng minh rằng (ảnh 1)

    * Ta có: BA = BC (gt)

    Suy ra B thuộc đường trung trực của AC

    *Và DC = DA (gt)

    Suy ra D thuộc đường trung trực của AC

    Mà B ≠ D nên BD là đường trung trực của AC.

    Do đó A đối xứng với C qua trục BD.

    Bài 66 trang 87 SBT Toán 8 Tập 1: Cho tam giác ABC có AB < AC. Gọi d là đường thẳng trung trực của BC. Vẽ điểm K đối xứng với điểm A qua đường thẳng d

    a) Tìm các đoạn thẳng đối xứng với đoạn thẳng AB qua d, đối xứng với đoạn thẳng AC qua d.

    b) Tứ giác AKCB là hình gì? Vì sao?

    Lời giải:

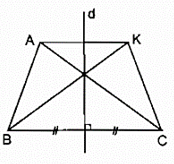
    Cho tam giác ABC có AB < AC. Gọi d là đường thẳng trung trực của BC (ảnh 1)

    a) Vì d là đường thẳng trung trực của BC nên B và C đối xứng qua d

    K đối xứng với A qua d

    Nên đoạn thẳng đối xứng với đoạn AB qua d là đoạn KC

    Suy ra: Đoạn thẳng đối xứng với đoạn AC qua d là đoạn KB.

    b) d là đường trung trực của BC (gt)

    ⇒ d ⊥ BC

    A và K đối xứng qua d nên d là trung trực của AK

    ⇒ d ⊥ AK

    Suy ra: BC //AK. Do đó, tứ giác ABCK là hình thang.

    Vì AC và KB đối xứng qua d nên AC = BK

    Vậy hình thang ABCK là hình thang cân.

    Bài 67 trang 87 SBT Toán 8 Tập 1: Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C). Chứng minh rằng AC + CB < AM + MB

    Lời giải:

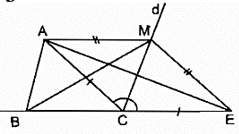
    Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (ảnh 1)

    Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ΔACE cân tại C có CM là đường phân giác nên CM là đường trung trực (tính chất tam giác cân).

    ⇒ MA = ME (tính chất đường trung trực).

    Ta có: AC + BC = CE + BC = BE (1)

    MA + MB = ME + MB (2)

    Trong ΔMBE, ta có:

    BE < MB+ ME (bất đẳng thức tam giác) (3)

    Từ (1), (2) và (3) suy ra:

    AC + CB < AM + MB.

    Bài 68 trang 87 SBT Toán 8 Tập 1: Trong các hình nét đậm vẽ trên giấy kẻ ô vuông ở hình 4, hình 5, hình nào có trục đối xứng.

    Lời giải:

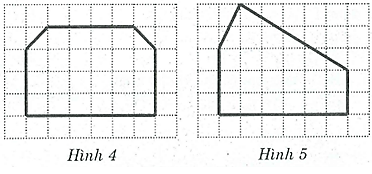
    Trong các hình nét đậm vẽ trên giấy kẻ ô vuông ở hình 4, hình 5 (ảnh 1)

    Hình 4 là hình có trục đối xứng.

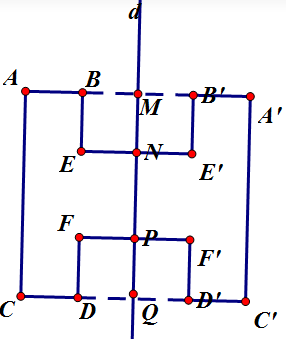
    Bài 69 trang 88 SBT Toán 8 Tập 1: Vẽ hình đối xứng qua đường thẳng d của hình đã vẽ (h.6)

    Lời giải:

    a)

    - Kéo dài AB, CD cắt d tại M, Q

    - Trên tia AB lấy A', B' sao cho MB' = MB; MA' = MA

    - Trên tia CD lấy C', D' sao cho QC' = QC; QD' = QD

    - Trên tia EN lấy E' sao cho NE = NE'

    - Trên tia FP lấy F' sao cho PF = PF'

    Nối các điểm đã dựng ta được hình đối xứng qua d của hình đã cho.

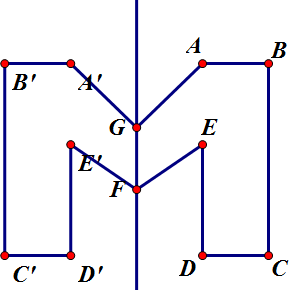
    Vẽ hình đối xứng qua đường thẳng d của hình đã vẽ (ảnh 1)

    b)

    Gọi tên như hình vẽ dưới đây.

    - Vẽ A’ đối xứng với A qua đường thẳng d, vẽ B’ đối xứng với B qua đường thẳng d.

    - Nối A’B’; A’G

    - Vẽ E’ đối xứng với E qua đường thẳng d, nối E’F

    - Vẽ C’ đối xứng với C qua đường thẳng d, vẽ D’ đối xứng với D qua đường thẳng d.

    - Nối E’D”, C’D’, C’B’ ta được hình đối xứng với hình đã cho qua d.

    Vẽ hình đối xứng qua đường thẳng d của hình đã vẽ (ảnh 1)Bài 70 trang 88 SBT Toán 8 Tập 1: Điền dấu “X” vào ô thích hợp:

    Câu khẳng định

    Đúng

    Sai

    a) Tam giác có một trục đối xứng là tam giác cân

    		    

    b) Tứ giác có một trục đối xứng là hình thang cân

    		    

    Lời giải:

    Câu khẳng định

    Đúng

    Sai

    a) Tam giác có một trục đối xứng là tam giác cân

    X

    		  

    b) Tứ giác có một trục đối xứng là hình thang cân

    		  

    X

    Bài 71 trang 88 SBT Toán 8 Tập 1: Chứng minh rằng giao điểm hai đường chéo hình thang cân nằm trên trục đối xứng của hình thang cân.

    Lời giải:

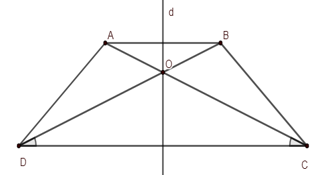
    Chứng minh rằng giao điểm hai đường chéo hình thang cân (ảnh 1)

    Hình thang cân ABCD có AB // CD.

    Gọi O là giao điểm của hai đường chéo AC và BD.

    Xét ΔADC và ΔBCD:

    AD = BC (tính chất hình thang cân)

    AC = BD (tính chất hình thang cân)

    CD chung

    Do đó ΔADC= ΔBCD (c.c.c)

    ⇒ ODC^ = OCD^ (hai góc tương ứng)

    ⇒ΔOCD cân tại O

    ⇒ OC = OD nên O nằm trên đường trung trực của CD.

    Trục đối xứng hình thang cân là đường thẳng trung trực của hai đáy.

    Vậy O thuộc trục đối xứng của hình thang cân.

    Bài 72 trang 88 SBT Toán 8 Tập 1: Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.

    Lời giải:

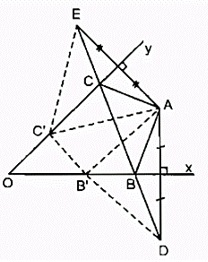
    Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox (ảnh 1)

    Cách dựng:

    - Dựng điểm D đối xứng với A qua Ox

    - Dựng điểm E đối xứng với A qua Oy

    Nối DE cắt Ox tại B, Oy tại C

    Tam giác ABC là tam giác có chu vi nhỏ nhất

    Vì xOy^ < 90o nên DE luôn cắt Ox và Oy do đó ΔABC luôn dựng được.

    Chứng minh:

    Chu vi ΔABC bằng AB + BC + AC

    Vì D đối xứng với A qua Ox nên Ox là trung trực của AD

    ⇒ AB = BD (tính chất đường trung trực)

    E đối xứng với A qua Oy nên Oy là trung trực của AE

    ⇒ AC = CE (tính chất đường trung trực)

    Suy ra:

    AB + BC + AC = BD + BC + BE = DE (1)

    Lấy B' bất kì trên Ox, C' bất kì trên tia Oy. Nối C'E, C'A, B'A, B'D.

    Ta có: B'A = B'D và C'A = C'E (tính chất đường trung trực)

    Chu vi ΔAB'C' bằng AB'+ AC’ + B'C'= B'D+C’E+ B'C' (2)

    Vì DE ≤ B'D + C’E+ B'C' (dấu bằng xảy ra khi B' trùng B, C' trùng C) nên chu vi của ΔABC ≤ chu vi của ΔA'B'C'

    Vậy ΔABC có chu vi bé nhất.

    Bài tập bổ sung

    Bài 6.1 trang 88 SBT Toán 8 Tập 1: Hãy nối mỗi cột của ô bên trái với một ô của cột bên phải để được khẳng định đúng...

    Bài 6.2 trang 88 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 7: Hình bình hành

    Bài 8: Đối xứng tâm

    Bài 9: Hình chữ nhật

    Bài 10: Đường thẳng song song với một đường thẳng cho trước

    Bài 11: Hình thoi

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Đối xứng trục có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,185 18/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: