SBT Toán 8 Bài 3: Tính chất đường phân giác của tam giác

Mục lục Giải SBT Toán 8 Bài 3: Tính chất đường phân giác của tam giác

Bài 17 trang 87 SBT Toán 8 Tập 2: Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D.

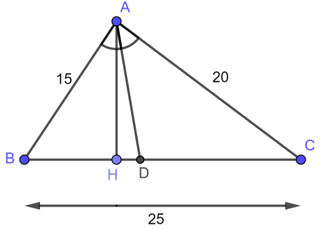
a) Tính độ dài các đoạn thẳng DB và DC.

b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

Lời giải:

a) Trong ΔABC, ta có: AD là đường phân giác của góc BAC.

Suy ra: $\frac{DB}{DC}=\frac{AB}{AC}$ (tính chất đường phân giác)

Mà AB = 15 (cm); AC = 20 (cm)

Nên $\frac{DB}{DC}=\frac{15}{20}$

Suy ra: $\frac{DB}{DB+DC}=\frac{15}{15+\text{\hspace{0.17em}}20}$ (tính chất tỉ lệ thức)

Suy ra:

$$\begin{gathered} \frac{DB}{BC}=\frac{15}{35} \\ \Rightarrow DB\text{\hspace{0.17em}}=\frac{15}{35}.25=\frac{75}{7}cm \end{gathered}$$

 Do đó, DC = BC – BD = $25-\frac{75}{7}=\frac{100}{7}cm$

b) Kẻ AH ⊥ BC

Ta có: S_ABD =  $\frac{1}{2}$AH.BD; S_ADC = $\frac{1}{2}$AH.DC.

Suy ra: $\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}$

Mà $\frac{DB}{DC}=\frac{15}{20}=\frac{3}{4}$ ( chứng minh trên)

Vậy $\frac{S_{ABD}}{S_{ADC}}=\frac{BD}{DC}\text{\hspace{0.17em}\hspace{0.17em}}=\frac{3}{4}$.

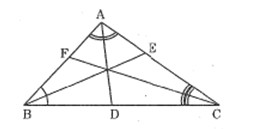
Bài 18 trang 87 SBT Toán 8 Tập 2: Tam giác ABC có các đường phân giác AD, BE, CF.

Chứng minh rằng: $\frac{DB}{DC}.\frac{EC}{EA}.\frac{FA}{FB}=1$ .

Lời giải:

Trong ΔABC, ta có: AD là đường phân giác của góc BAC

Suy ra: $\frac{DB}{DC}=\frac{AB}{AC}$ (tính chất đường phân giác) (1)

BE là đường phân giác của góc ABC

Suy ra: $\frac{EC}{EA}=\frac{BC}{AB}$ (tính chất đường phân giác) (2)

CF là đường phân giác của góc ACB

Suy ra: $\frac{FA}{FB}=\frac{CA}{CB}$ (tính chất đường phân giác) (3)

Nhân từng vế (1), (2) và (3) ta có:

$\frac{DB}{DC}.\frac{EC}{EA}.\frac{FA}{FB}=\frac{AB}{AC}.\frac{BC}{AB}.\frac{CA}{CB}=1$

 (điều phải chứng minh).

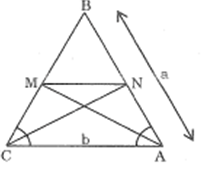
Bài 19 trang 87 SBT Toán 8 Tập 2: Tam giác cân ABC có BA = BC = a, AC = b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N.

a) Chứng minh MN // AC;

b) Tính MN theo a, b.

Lời giải:

a) Trong ΔBAC, ta có: AM là đường phân giác của $\widehat{BAC}$

Suy ra: $\frac{MC}{MB}=\frac{AC}{AB}$ (tính chất đường phân giác) (1)

CN là đường phân giác của $\widehat{BCA}$.

Suy ra: $\frac{NA}{NB}=\frac{AC}{CB}$ (tính chất đường phân giác) (2)

Lại có: AB = CB = a (gt)

Từ (1), (2) và (gt) suy ra: $\frac{NA}{NB}=\frac{MC}{MB}$

Trong ΔBAC, ta có: $\frac{NA}{NB}=\frac{MC}{MB}$ .

Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét).

b) Ta có: $\frac{MC}{MB}=\frac{AC}{AB}$ (chứng minh trên)

Suy ra: 

$$\begin{gathered} \frac{MC+\text{\hspace{0.17em}\hspace{0.17em}}MB}{MB}=\frac{AC+\text{}AB}{AB} \\ \Rightarrow \frac{CB}{MB}=\frac{AC+\text{}AB}{AB} \end{gathered}$$

Hay $\frac{a}{MB}=\frac{b+\text{}a}{a}\Rightarrow MB\text{\hspace{0.17em}\hspace{0.17em}}=\frac{a^2}{a+\text{\hspace{0.17em}\hspace{0.17em}}b}$ .

Trong ΔBAC, ta có:

MN //AC (chứng minh trên)

Suy ra: $\frac{MN}{AC}=\frac{MB}{BC}$

Vậy

$$\begin{gathered} MN=\frac{AC.MB}{BC}=\frac{b.\frac{a^2}{a+\text{\hspace{0.17em}\hspace{0.17em}}b}}{a} \\ =\frac{ab}{a+\text{\hspace{0.17em}\hspace{0.17em}}b} \end{gathered}$$

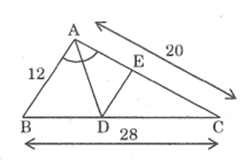
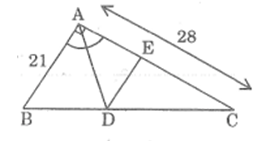
Bài 20 trang 87 SBT Toán 8 Tập 2: Tam giác ABC có AB = 12cm, AC = 20cm, BC = 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E ∈ AC).

a) Tính độ dài các đoạn thẳng BD, DC, DE.

b) Cho biết diện tích tam giác ABC là S, tính diện tích các tam ABD, ADE, DCE.

Lời giải:

a) Trong ΔABC, ta có: AD là đường phân giác của góc BAC

Suy ra: $\frac{DB}{DC}=\frac{AB}{AC}$  (tính chất tia phân giác)

Suy ra: $\frac{DB}{DB+\text{\hspace{0.17em}}DC}=\frac{AB}{AB+\text{\hspace{0.17em}}AC}$

Suy ra: $\frac{DB}{BC}=\frac{AB}{AB+\text{\hspace{0.17em}}AC}$ .

Suy ra:

$$\begin{gathered} DB=\frac{BC.AB}{AB+\text{\hspace{0.17em}\hspace{0.17em}}AC}=\frac{28.12}{12+\text{}20} \\ =\frac{21}{2}=10,5cm \end{gathered}$$ 

Vậy DC = BC - DB = 28 - 10,5 = 17,5 (cm)

* Trong ΔABC, ta có: DE // AB

Suy ra: $\frac{DC}{BC}=\frac{DE}{AB}$  (Hệ quả định lí Ta-lét)

Vậy: $DE=\frac{DC.AB}{BC}=\frac{17,5.12}{28}=7,5cm$

b) Vì ΔABD và ΔABC có chung đường cao kẻ từ đỉnh A nên

$\frac{S_{ABD}}{S_{ABC}}=\frac{BD}{BC}=\frac{10,5}{28}=\frac{3}{8}$

Vậy: S_ABD = $\frac{3}{8}$.S

S_ADC = S_ABC - S_ABD = S - $\frac{3}{8}S=\frac{5}{8}S$

Vì DE // AB và AD là đường phân giác góc A nên ta chứng minh được tam giác AED cân tại E, do đó AE = DE

Ta có: $\frac{S_{ADE}}{S_{ADC}}=\frac{AE}{AC}=\frac{DE}{AC}=\frac{7,5}{20}=\frac{3}{8}$

Vậy: $S_{ADE}=\frac{3}{8}{S}_{ADC}=\frac{3}{8}.\frac{5}{8}S=\frac{15}{64}\text{}S$

Ta có:

$$\begin{gathered} S_{DCE}=S_{ADC}-S_{ADE} \\ =\frac{5}{8}S\text{\hspace{0.17em}\hspace{0.17em}}-\frac{15}{64}S=\frac{25}{64}S \end{gathered}$$

Bài 21 trang 88 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thẳng qua D song song với AB cắt AC tại E.

a)Tính độ dài các đoạn thẳng BD, DC và DE.

b) Tính diện tích tam giác ABD và diện tích tam giác ACD.

Lời giải:

a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = 21² + 28² = 1225

Suy ra: BC = 35 (cm)

Vì AD là đường phân giác của góc BAC nên:

$\frac{BD}{DC}=\frac{AB}{AC}$ (t/chất đường phân giác)

Suy ra: $\frac{BD}{BD+\text{\hspace{0.17em}\hspace{0.17em}}DC}=\frac{AB}{AB+\text{\hspace{0.17em}}AC}$

Hay $\frac{BD}{BC}=\frac{AB}{AB+\text{\hspace{0.17em}}AC}$ .

Suy ra: 

$BD=\frac{BC.AB}{AB+\text{\hspace{0.17em}\hspace{0.17em}}AC}=\frac{35.21}{21+28}=15cm$

Vậy DC = BC – BD = 35 – 15 = 20cm

Trong ΔABC ta có: DE // AB

Suy ra: $\frac{DC}{BC}=\frac{DE}{AB}$  (Hệ quả định lí Ta-lét)

Suy ra: $DE\text{\hspace{0.17em}\hspace{0.17em}}=\frac{DC.\text{}AB}{BC}=\frac{20.21}{35}=12cm$ 

b) Ta có: S_ABC = $\frac{1}{2}$.AB.AC = $\frac{1}{2}$.21.28 = 294 (cm²)

Vì ΔABC và ΔADB có chung đường cao kẻ từ đỉnh A nên:

$$\begin{gathered} \frac{S_{ADB}}{S_{ABC}}=\frac{BD}{BC}=\frac{15}{35}=\frac{3}{7} \\ \Rightarrow S_{ADB}=\frac{3}{7}{S}_{ABC} \\ =\frac{3}{7}.294=126 \left(c{m}^2\right) \end{gathered}$$

Vậy S_ADC = S_ABC – S_ABD = 294 – 126 = 168(cm²).

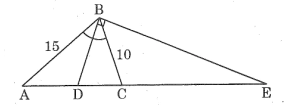
Bài 22 trang 88 SBT Toán 8 Tập 2: Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm.

a) Tính AD, DC.

b) Đường vuông góc với BD tại B cắt đường thẳng AC tại E. Tính EC.

Lời giải:

Vì BD là đường phân giác của góc ABC nên:

$\frac{AD}{DC}=\frac{AB}{BC}$ (t/chất đường phân giác)

Suy ra: $\frac{AD}{AD+\text{}DC}=\frac{AB}{AB+\text{\hspace{0.17em}\hspace{0.17em}}BC}$ hay $\frac{AD}{AC}=\frac{AB}{AB+\text{\hspace{0.17em}\hspace{0.17em}}BC}$

Mà ΔABC cân tại A nên AC = AB = 15 (cm)

Suy ra: $\frac{AD}{15}=\frac{15}{15+\text{}10}\Rightarrow AD=\frac{15.15}{15+10}=9$(cm)

Vậy DC = AC – AD = 15 – 9 = 6 (cm)

b) Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B

Suy ra : $\frac{E\text{}C}{EA}=\text{}\frac{BC}{BA}$( t/chất đường phân giác)

Suy ra: $\frac{E\text{}C}{EC+\text{}CA}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{BC}{BA}$  ⇒ EC.BA= BC (EC + AC)

Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC

Vậy $EC=\frac{BC.AC}{BA\text{}-BC}=\frac{10.15}{15-10}=30\left(cm\right)$ .

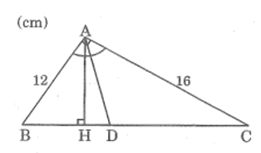
Bài 23 trang 88 SBT Toán 8 Tập 2: Tam giác ABC có góc A = 90^o, AB = 12cm, AC =16cm; đường phân giác góc A cắt BC tại D.

a) Tính BC, BD và DC.

b) Kẻ đường cao AH, tính AH, HD và AD.

Lời giải:

a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = 12² + 16² = 400

Suy ra: BC = 20 (cm)

Vì AD là đường phân giác của góc BAC nên:

 $\frac{DB}{DC}=\frac{AB}{AC}$ (tính chất đường phân giác)

Suy ra: $\frac{DB}{DB+\text{\hspace{0.17em}}DC}=\frac{AB}{AB\text{}+\text{\hspace{0.17em}\hspace{0.17em}}AC}$hay $\frac{DB}{BC}=\frac{AB}{AB\text{}+\text{\hspace{0.17em}\hspace{0.17em}}AC}$

Suy ra: $DB\text{\hspace{0.17em}\hspace{0.17em}}=\frac{BC.AB}{AB+\text{\hspace{0.17em}\hspace{0.17em}}AC}=\frac{20.12}{12+\text{}16}=\frac{60}{7}$(cm)

Vậy : DC = BC – DB

= 20 - $\frac{60}{7}=\frac{80}{7}$ (cm)

b) Ta có: S_ABC = $\frac{1}{2}$.AB.AC = $\frac{1}{2}$.AH.BC.

Suy ra: AB.AC = AH.BC

$\Rightarrow AH=\frac{AB.\text{}AC}{BC}=\frac{12.16}{20}=9,6$ (cm)

Trong tam giác vuông AHB,

ta có: $\widehat{AHB}$ = 90^o

Theo định lí Pi-ta-go, ta có:

AB² = AH² + HB²

Suy ra:

HB² = AB² - AH² = 12² - (9,6)² 

= 51,84 ⇒ HB =7,2 (cm)

Vậy HD = BD – HB =  - 7,2 ≈ 1,37 (cm)

Trong tam giác vuông AHD,

ta có: $\widehat{AHD}$ = 90^o

Theo định lí Pi-ta-go, ta có:

AD² = AH² + HD² 

= (9,6)² + (1,37)² = 94,0369

Suy ra: AD ≈ 9,70 (cm).

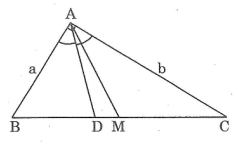
Bài 24 trang 88 SBT Toán 8 Tập 2: Tam giác ABC có $\hat{A}$ = 90°, AB = a (cm), AC = b (cm) (a < b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC).

a) Tính độ dài các đoạn thẳng BC, BD, DC, AM và DM theo a, b

b) Hãy tính độ dài các đoạn thẳng trên chính xác đến chữ số thập phân thứ hai khi biết a = 4,15cm, b = 7,25cm.

Lời giải:

a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = a² + b²

Suy ra: $BC\text{\hspace{0.17em}\hspace{0.17em}}=\sqrt{a^2\text{}+\text{\hspace{0.17em}\hspace{0.17em}}{b}^2}$.

Ta có: AM = BM = $\frac{1}{2}$.BC (tính chất đường trung tuyến ứng với cạnh huyền).

Suy ra: AM $=\frac{1}{2}\sqrt{a^2\text{}+\text{\hspace{0.17em}\hspace{0.17em}}{b}^2}$

Vì AD là đường phân giác của góc BAC nên:

$\frac{DB}{DC}=\frac{AB}{AC}$ (tính chất đường phân giác)

Suy ra: $\frac{DB}{DB+\text{\hspace{0.17em}}DC}=\frac{AB}{AB+AC}$

hay

$$\begin{gathered} \frac{DB}{BC}=\frac{AB}{AB+AC} \\ \Rightarrow DB=\frac{BC.AB}{AB+\text{\hspace{0.17em}}AC}=\frac{a\sqrt{a^2\text{}+\text{\hspace{0.17em}}{b}^2}}{a+\text{}b} \end{gathered}$$

Vậy

$$\begin{gathered} DC=BC-DB \\ =\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}-\frac{a.\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}}{a+b} \\ =\frac{b.\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}}{a+b} \end{gathered}$$

$\begin{array}{l}DM=BM-BD\\ =\frac{1}{2}\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}-\frac{a.\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}}{a+b}\\ =\frac{(a+\text{}b).\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}}{2(a+b)}-\frac{2a.\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}}{2(a+b)}\\ \hspace{0.17em}=\frac{(b-a).\sqrt{a^2+\text{\hspace{0.17em}}{b}^2}}{2(a+b)}\end{array}$

b) Với a = 4,15 (cm); b = 7,25 (cm), sử dụng máy tính và các kết quả ý a, ta tính được:

BC ≈ 8,35 cm

BD ≈ 3,04 cm

DC ≈ 5,31 cm

AM ≈ 4,18 cm

DM ≈ 1,14cm

Bài tập bổ sung

Bài 3.1 trang 89 SBT Toán 8 Tập 2: Tam giác ABC vuông tại A có đường phân giác AD. Biết rằng độ dài của các cạnh góc vuông...

Bài 3.2 trang 89 SBT Toán 8 Tập 2: Hình bình hành ABCD có độ dài cạnh AB = a = 12,5cm, BC = b = 7,25cm. Đường phân giác...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 4: Khái niệm hai tam giác đồng dạng

Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)

Bài 6: Trường hợp đồng dạng thứ hai (c.g.c)

Bài 7: Trường hợp đồng dạng thứ ba (g.g)

Bài 8: Các trường hợp đồng dạng của tam giác vuông

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Lý thuyết Tính chất đường phân giác của tam giác

Trắc nghiệm Tính chất đường phân giác của tam giác có đáp án