Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 3: Bất phương trình một ẩn

    Với giải sách bài tập Toán lớp 8 Bài 3: Bất phương trình một ẩn chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 951 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Bài 3: Bất phương trình một ẩn

    Bài 31 trang 54 SBT Toán 8 Tập 2: Kiểm tra xem các giá trị sau đây của x có là nghiệm của bất phương trình x2 – 2x < 3x hay không:

    a) x = 2;

    b) x = 1;

    c) x = –3;

    d) x = 4.

    Lời giải:

    a) Thay x = 2 vào bất phương trình ta được:

    22 – 2.2 < 3.2 hay 0 < 6 ( thỏa mãn)

    Vậy x = 2 là nghiệm của bất phương trình.

    b) Thay x = 1 vào bất phương trình ta được:

    12 – 2.1 < 3.1 hay –1 < 3 ( thỏa mãn)

    Vậy x = 1 là nghiệm của bất phương trình.

    c) Thay x = –3 vào bất phương trình ta được:

    (–3)2 – 2.(–3) < 3.(–3)  hay 15 < – 9 ( vô lí)

    Vậy x = –3 không là nghiệm của bất phương trình.

    d) Thay x = 4 vào bất phương trình ta được:

    42 – 2.4 < 3.4 hay 8 < 12 (thỏa mãn)

    Vậy x = 4 là nghiệm của bất phương trình.

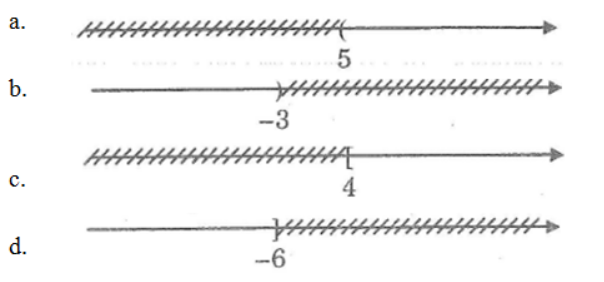
    Bài 32 trang 54 SBT Toán 8 Tập 2: Biểu diễn tập nghiệm của bất phương trình sau trên trục số:

    a) x > 5

    b) x < –3

    c) x ≥ 4

    d) x ≤ – 6

    Lời giải:

    Tài liệu VietJack

    Bài 33 trang 54 SBT Toán 8 Tập 2: Cho tập A = {–10; –9; –8; –7; – 6 ; –5; – 4;……; 8; 9; 10}. Hãy cho biết giá trị nào của x trong tập A sẽ là nghiệm của bất phương trình.

    a) |x| < 3;

    b) |x| > 8;

    c) |x| ≤ 4;

    d) |x| ≥ 7.

    Lời giải:

    a) Ta có: |x| < 3 ⇔ –3 < x < 3

    Các giá trị trong tập hợp A là nghiệm của bất phương trình là:

    –2; –1; 0; 1; 2

    b) Ta có: |x| > 8 ⇔ x > 8 hoặc x < –8

    Các giá trị trong tập hợp A là nghiệm của bất phương trình là:

    –10; –9; 9; 10

    c) Ta có: |x| ≤ 4 ⇔ –4 ≤ x ≤ 4

    Các số trong tập hợp A là nghiệm của bất phương trình là:

    –4; –3; –2; –1; 0; 1; 2; 3; 4

    d) Ta có: |x| ≥ 7 ⇔ x ≥ 7 hoặc x ≤ –7

    Các số trong tập hợp A là nghiệm của bất phương trình là:

    –10; –9; –8; –7; 7; 8; 9; 10

    Bài 34 trang 54 SBT Toán 8 Tập 2: Hãy đưa ra hai số nguyên là nghiệm của bất phương trình sau:

    a) –4x + 5 > 10;

    b) 2x + 100 < 90;

    Lời giải:

    a) Ta có: x = – 4 và x = –3 là nghiệm của bất phương trình vì:

    – 4.(– 4) + 5 = 16 + 5 = 21 và 21 > 10

    – 4.(– 3) + 5 = 12 + 5 = 17 và 17 > 10

    b) Ta có: x = – 10 và x = – 20 là nghiệm của bất phương trình vì:

    2.(– 10) + 100 = – 20 + 100 = 80

    và 80 <  90.

    2.(– 20) + 100 = – 40 + 100 = 60

    và 60 < 90.

    Bài 35 trang 55 SBT Toán 8 Tập 2: Viết thành bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau đây:

    a) Tổng của số nào đó và 5 lớn hơn 7.

    b) Hiệu của 9 và số nào đó nhỏ hơn –12.

    Lời giải:

    a) Theo đầu bài ta có bất phương trình:

    x + 5 > 7

    Ta có x = 3 là nghiệm của bất phương trình

    vì 3 + 5 = 8 và 8 > 7.

    b) Ta có bất phương trình 9 – x < –12

    Ta có x = 22 là nghiệm của bất phương trình

    vì 9 – 22 = –13 và – 13 < –12.

    Bài 36 trang 55 SBT Toán 8 Tập 2: Viết thành bất phương trình và chỉ ra hai nghiệm của nó từ các mệnh đề sau đây:

    a) Tổng của 2 lần số nào đó và 3 lớn hơn 12.

    b) Hiệu của 5 và 3 lần số nào đó nhỏ hơn 10.

    Lời giải:

    a) Ta có bất phương trình 2x + 3 > 12

    Và x = 6 và x = 7 là nghiệm của bất phương trình vì:

    2.6 + 3 = 15 > 12 và 2.7 + 3 = 17 > 12

    b) Ta có bất phương trình 5 – 3x < 10

    Và x = 1 và x = 2 là nghiệm của bất phương trình vì:

    5 – 3.1 = 2 < 10 và 5 – 3.2 = –1 < 10

    Lời giải:

    a) Theo đầu bài ta có bất phương trình:

    x + 5 > 7

    Ta có x = 3 là nghiệm của bất phương trình

    vì 3 + 5 = 8 và 8 > 7.

    b) Ta có bất phương trình 9 – x < –12

    Ta có x = 22 là nghiệm của bất phương trình

    vì 9 – 22 = –13 và – 13 < –12.

    Bài 37 trang 55 SBT Toán 8 Tập 2: Cho tập A = {–10; –9; –8; –7;…..; 8; 9; 10}. Hãy cho biết số nào trong A là nghiệm của bất phương trình.

    a) |x – 2| ≤ 3;

    b) |x – 3| > 5.

    Lời giải:

    a) Ta có: |x – 2| ≤ 3

    ⇔ –3 ≤ x – 2 ≤ 3

    ⇔ –1 ≤ x ≤ 5

    Các số trong tập hợp A là nghiệm của bất phương trình là:

    –1; 0; 1; 2; 3; 4; 5

    b) Ta có: |x – 3| > 5

    ⇒ (x – 3 > 5) hoặc (x – 3 < –5)

    ⇔ x > 8 hoặc x < –2.

    Các số trong tập hợp A là nghiệm của bất phương trình là:

    10; 9; –3; –4; –5; –6; –7; –8; –9; –10.

    Bài 38 trang 55 SBT Toán 8 Tập 2: Hãy đưa ra ba nghiệm của bất phương trình:

    a) 5 > x;

    b) –4 < x.

    Lời giải:

    a) Ta có:  5 > 3; 5 > 2 và 5 > 1.

     Do đó, các số 3; 2; 1 là nghiệm của bất phương trình.

    b) Ta có: – 4 < –3; – 4 < – 2; –4 < –1

     Do đó, các số –3; –2; –1 là nghiệm của bất phương trình.

    Bài 39 trang 55 SBT Toán 8 Tập 2: Viết tập hợp nghiệm của bất phương trình sau bằng kí hiệu tập hợp và biểu diễn tập nghiệm trên trục số.

    a) 2 > x ;

    b) –3 < x .

    Lời giải:

    a) Viết tập hợp nghiệm của bất phương trình bằng kí hiệu tập hợp:

     S ={x| x < 2}.

    Biểu diễn tập nghiệm trên trục số.

    Tài liệu VietJack

    b. Viết tập hợp nghiệm của bất phương trình bằng kí hiệu tập hợp:

    S = {x| x > –3}.

    Biểu diễn tập nghiệm trên trục số.

    Tài liệu VietJack

    Bài tập bổ sung

    Bài 3.1 trang 55 SBT Toán 8 Tập 2: Khoanh vào chữ cái trước khẳng định đúng...

    Bài 3.2 trang 55 SBT Toán 8 Tập 2: Khoanh vào chữ cái trước hình đúng Hình biểu diễn tập nghiệm của bất phương trình...

    Bài 3.3 trang 56 SBT Toán 8 Tập 2: Lập bất phương trình cho bài toán sau...

    Xem thêm lời giải sách bài tập Toán học lớp 8 hay, chi tiết khác:

    Bài 1: Liên hệ giữa thứ tự và phép cộng

    Bài 2: Liên hệ giữa thứ tự và phép nhân

    Bài 4: Bất phương trình bậc nhất một ẩn

    Bài 5: Phương trình chứa dấu giá trị tuyệt đối

    Ôn tập chương 4

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Bất phương trình một ẩn

    Trắc nghiệm Bất phương trình một ẩn có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 951 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: