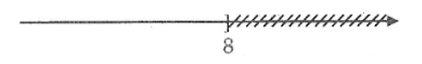SBT Toán 8 Bài 4: Bất phương trình bậc nhất một ẩn

Mục lục Giải SBT Toán 8 Bài 4: Bất phương trình bậc nhất một ẩn

Bài 40 trang 56 SBT Toán 8 Tập 2: Áp dụng quy tắc chuyển vế để giải các bất phương trình sau:

a) x – 2 > 4;

b) x + 5 < 7;

c) x – 4 < –8;

d) x + 3 > – 6.

Lời giải:

a) Ta có: x – 2 > 4

⇔ x > 4 + 2 ⇔ x > 6

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 6}.

b) Ta có: x + 5 < 7

⇔ x < 7 – 5 ⇔ x < 2

Vậy tập nghiệm của bất phương trình là:

S = {x| x < 2}.

c) Ta có: x – 4 < –8

⇔ x < –8 + 4 ⇔ x < – 4

Vậy tập nghiệm của bất phương trình là:

S = {x| x < –4}.

d) Ta có: x + 3 > –6

⇔ x > –6 – 3 ⇔ x > –9.

Vậy tập nghiệm của bất phương trình là:

S = {x| x > –9}.

Bài 41 trang 56 SBT Toán 8 Tập 2: Áp dụng quy tắc chuyển vế, giải các bất phương trình sau:

a) 3x < 2x + 5;

b) 2x + 1 < x + 4;

c) –2x > –3x + 3;

d) –4x – 2 > –5x + 6.

Lời giải:

a) Ta có: 3x < 2x + 5

⇔ 3x – 2x < 5 ⇔ x < 5

Vậy tập nghiệm của bất phương trình là:

S= {x| x < 5}.

b) Ta có: 2x + 1 < x + 4

⇔ 2x – x < 4 – 1 ⇔ x < 3

Vậy tập nghiệm của bất phương trình là:

S = {x| x < 3}.

c) Ta có: –2x > –3x + 3

⇔ –2x + 3x > 3 ⇔ x > 3

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 3}.

d) Ta có: –4x – 2 > –5x + 6

⇔ –4x + 5x > 6 + 2 ⇔ x > 8

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 8}.

Bài 42 trang 56 SBT Toán 8 Tập 2: Áp dụng quy tắc nhân để giải các bất phương trình sau:

a) $\frac{1}{2}x>3$;

b) $\frac{-1}{3}x<-2$;

c) $\frac{2}{3}x>-4$;

d) $\frac{-3}{5}x>6$.

Lời giải:

a) Ta có: $\frac{1}{2}x>3$

 ⇔ $\frac{1}{2}x.2>3.2$ ⇔ x > 6.

Vậy tập nghiệm của bất phương trình là:

S =  {x| x > 6}.

b) Ta có: $\frac{-1}{3}x<-2$

⇔ $\frac{-1}{3}x.(-3)>-2.(-3)$ ⇔ x > 6

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 6}.

c) Ta có: $\frac{2}{3}x>-4$

⇔ $\frac{2}{3}x.\frac{3}{2}>-4.\frac{3}{2}$ ⇔ x > –6

Vậy tập nghiệm của bất phương trình là:

S = {x| x > –6}.

d) Ta có: $\frac{-3}{5}x>6$

⇔ $\frac{-3}{5}x.\left(\frac{-5}{3}\right)<6.\left(\frac{-5}{3}\right)$ ⇔ x < –10

Vậy tập nghiệm của bất phương trình là:

S = {x| x < –10}.

Bài 43 trang 56 SBT Toán 8 Tập 2: Áp dụng quy tắc nhân, giải các bất phương trình sau:

a) 3x < 18 ;

b) –2x > –6;

c) 0,2x > 8;

d) –0,3x < 12.

Lời giải:

a) Ta có: 3x < 18

$\iff 3x.\frac{1}{3}<18.\frac{1}{3}\iff x<6$

Vậy tập nghiệm của bất phương trình là:

S = {x| x < 6}.

b) Ta có: –2x > –6

$\iff (-2x).\left(\frac{-1}{2}\right)<(-6).\left(\frac{-1}{2}\right)\iff x<3$

Vậy tập nghiệm của bất phương trình là:

S = {x| x < 3}.

c) Ta có: 0,2x > 8

 ⇔ 0,2x.5 > 8.5 ⇔ x > 40.

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 40}.

d) Ta có: –0,3x < 12

$$\begin{gathered} \iff -0,3x.\left(\frac{-10}{3}\right)>12.\left(\frac{-10}{3}\right) \\ \iff x>-40 \end{gathered}$$

Vậy tập nghiệm của bất phương trình là:

S = {x| x > –40}.

Bài 44 trang 56 SBT Toán 8 Tập 2: Giải thích sự tương đương:

a) 2x < 3 ⇔ 3x < 4,5;

b) x – 5 < 12 ⇔ x + 5 < 22;

c) –3x < 9 ⇔ 6x > –18.

Lời giải:

a) Nhân hai vế của bất phương trình 2x < 3 với 1,5.

b) Cộng hai vế của bất phương trình x – 5 < 12 với 10.

c) Nhân hai vế của bất phương trình –3x < 9 với –2.

Bài 45 trang 56 SBT Toán 8 Tập 2: Cho hình vẽ:

Bạn An cho rằng, hình vẽ đó biểu diễn tập nghiệm của bất phương trình 2x ≤ 16, còn bạn Bình lại khẳng định hình vẽ đó biểu diễn tập nghiệm của bất phương trình x + 2 ≤ 10. Theo em bạn nào đúng?

Lời giải:

Ta có: 2x ≤ 16 ⇔ x ≤ 8

x + 2 ≤ 10 ⇔ x ≤ 8

Như vậy cả hai bạn đều phát biểu đúng.

Bài 46 trang 57 SBT Toán 8 Tập 2: Giải các bất phương trình và biểu diễn tập nghiệm trên trục số

a) 2x – 4 < 0 ;

b) 3x + 9 > 0;

c) –x + 3 < 0;

d) –3x + 12 > 0.

Lời giải:

a)Ta có: 2x – 4 < 0

⇔ 2x < 4 ⇔ x < 2

Vậy tập nghiệm của bất phương trình là

S = {x | x < 2}

Biểu diễn tập nghiệm trên trục số

b) Ta có: 3x + 9 > 0

⇔ 3x > –9 ⇔ x > –3

Vậy tập nghiệm của bất phương trình là

S = {x | x > - 3}

Biểu diễn tập nghiệm trên trục số

c) Ta có: –x + 3 < 0

⇔ –x < –3 ⇔ x > 3.

Vậy tập nghiệm của bất phương trình là

S = {x | x > 3}

Biểu diễn tập nghiệm trên trục số

d) Ta có: –3x + 12 > 0

⇔ –3x > –12 ⇔ x < 4

Vậy tập nghiệm của bất phương trình là

S = {x | x < 4|}

Biểu diễn tập nghiệm trên trục số:

Bài 47 trang 57 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) 3x + 2 > 8;

b) 4x – 5 < 7;

c) – 2x + 1 < 7;

d) 13 – 3x > – 2.

Lời giải:

a) 3x + 2 > 8 $\iff$ 3x > 8 – 2

$\iff$ 3x > 6 $\iff x>2$

Vậy tập nghiệm của bất phương trình là

S = {x | x > 2}.

b) 4x – 5 < 7 $\iff$ 4x < 7 + 5

 $\iff$ 4x < 12 $\iff$ x < 3.

Vậy tập nghiệm của bất phương trình là

S = {x | x < 3}.

c) – 2x + 1 < 7 $\iff$ – 2x < 7 – 1

$\iff$ – 2x < 6 $\iff$ x > – 3

Vậy tập nghiệm của bất phương trình là

S = {x | x > – 3}.

d) 13 – 3x > – 2 $\iff$ – 3x > – 2 – 13

$\iff$ – 3x > – 15 $\iff$ x < 5

Vậy tập nghiệm của bất phương trình là

S = {x | x < 5}.

Bài 48 trang 57 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) $\frac{3}{2}x<-9$;

b) $5+\frac{2}{3}x>3$;

c) $2x+\frac{4}{5}>\frac{9}{5}$.

d) $6-\frac{3}{5}x<4$.

Lời giải:

a) Ta có: $\frac{3}{2}x<-9$

$\iff \frac{3}{2}x.\frac{2}{3}<-9.\frac{2}{3}\iff x<-6$

Vậy tập nghiệm của bất phương trình là:

S = {x| x < – 6}.

b) Ta có:

$\begin{array}{l}5+\frac{2}{3}x>3\iff \frac{2}{3}x>3-5\iff \frac{2}{3}x>-2\\ \iff \frac{2}{3}x.\frac{3}{2}>-2.\frac{3}{2}\iff x>-3\end{array}$

Vậy tập nghiệm của bất phương trình là:

S= {x| x > –3}.

c)Ta có: $2x+\frac{4}{5}>\frac{9}{5}$

$\iff 2x>\frac{9}{5}-\frac{4}{5}\iff 2x>1\iff x>\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{2}$

Vậy tập nghiệm của bất phương trình là:

S = {x| x > $\frac{1}{2}$}.

d) Ta có:

$\begin{array}{l}6-\frac{3}{5}x<4\iff -\frac{3}{5}x<4-6\\ \iff -\frac{3}{5}x<-2\\ \iff -\frac{3}{5}x.\frac{-5}{3}>-2.\frac{-5}{3}\iff x>\frac{10}{3}\end{array}$

Vậy tập nghiệm của bất phương trình là:

S = {x| x > $\frac{10}{3}$}.

Bài 49 trang 57 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) 7x – 2,2 < 0,6;

b) 1,5 > 2,3 – 4x.

Lời giải:

a) Ta có: 7x – 2,2 < 0,6

⇔ 7x < 0,6 + 2,2

⇔ 7x < 2,8

⇔ x < 0,4

Vậy tập nghiệm của bất phương trình là:

S = {x| x < 0,4}.

b) Ta có: 1,5 > 2,3 – 4x

⇔ 4x > 2,3 – 1,5

⇔ 4x > 0,8

⇔ x > 0,2

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 0,2}.

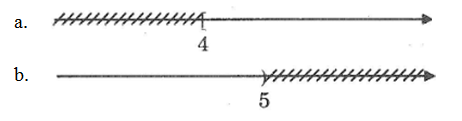
Bài 50 trang 57 SBT Toán 8 Tập 2: Viết bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ.

Lời giải:

a) Bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ là:

2x – 8 ≥ 0

Vì 2x – 8 ≥ 0 ⇔ 2x ≥ 8⇔ x ≥ 4

b) Bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ là:

3x – 15 < 0

Vì 3x – 15 < 0 ⇔  3x <  15⇔ x < 5.

Bài 51 trang 57 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) $\frac{3x-1}{4}>2$;

b) $\frac{2x+4}{3}\text{\hspace{0.17em}\hspace{0.17em}}<3$;

c) $\frac{1-2x}{3}>4$;

d) $\frac{6-4x}{5}<1$.

Lời giải:

a)Ta có: $\frac{3x-1}{4}>2$

⇔ 3x – 1 > 8

⇔ 3x > 8 + 1

⇔ 3x > 9 ⇔ x > 3

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 3}.

b) Ta có: $\frac{2x+4}{3}\text{\hspace{0.17em}\hspace{0.17em}}<3$

$\iff \frac{2x+4}{3}\text{\hspace{0.17em}\hspace{0.17em}}.3<3.3$

⇔ 2x + 4 < 9

⇔ 2x < 9 – 4

⇔ 2x < 5 ⇔ x < 2,5

Vậy tập nghiệm của bất phương trình là:

S =  {x| x < 2,5}.

c) Ta có: $\frac{1-2x}{3}>4$

$\iff \frac{1-2x}{3}.3>4.3$

⇔ 1 – 2x > 12

⇔ –2x > 12 – 1

⇔ –2x > 11 ⇔ x < –5,5

Vậy tập nghiệm của bất phương trình là:

S = {x| x < –5,5}.

d) Ta có: $\frac{6-4x}{5}<1$

$\iff \frac{6-4x}{5}.5<1.5$

⇔ 6 – 4x < 5

⇔ –4x < 5 – 6

⇔ –4x < –1 ⇔ $x>\frac{1}{4}$.

Vậy tập nghiệm của bất phương trình là:

S = {x| $x>\frac{1}{4}$ }.

Bài 52 trang 57 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) (x – 1)² < x(x + 3);

b) (x – 2)(x + 2) > x(x – 4);

c) 2x + 3 < 6 – (3 – 4x);

d) –2 – 7x > (3 + 2x) – (5 – 6x).

Lời giải:

a) Ta có: (x – 1)² < x(x + 3)

⇔ x² – 2x + 1 < x² + 3x

⇔ x² – 2x + 1 – x² – 3x < 0

⇔ –5x + 1 < 0 ⇔ 5x > 1 ⇔ $x>\frac{1}{5}$.

Vậy tập nghiệm của bất phương trình là:

S = {x| $x>\frac{1}{5}$}.

b) Ta có: (x – 2)(x + 2) > x(x – 4)

⇔ x² – 4 > x² – 4x

⇔ x² – 4 – x² + 4x > 0

⇔ 4x – 4 > 0 ⇔ x > 1

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 1}.

c) Ta có: 2x + 3 < 6 – (3 – 4x)

⇔ 2x + 3 < 6 – 3 + 4x

⇔ 2x – 4x < 3 – 3

⇔ –2x < 0 ⇔ x > 0

Vậy tập nghiệm của bất phương trình là:

S = {x| x > 0}.

d) Ta có: –2 – 7x > (3 + 2x) – (5 – 6x)

⇔ –2 – 7x > 3 + 2x – 5 + 6x

⇔ –7x – 2x – 6x > 3 – 5 + 2

⇔ –15x > 0 ⇔ x < 0

Vậy tập nghiệm của bất phương trình là:

S = {x| x < 0}.

Bài 53 trang 57 SBT Toán 8 Tập 2: Với các giá trị nào của x thì:

a) Giá trị phân thức $\frac{5-2x}{6}$ lớn hơn giá trị phân thức $\frac{5-2x}{3}$.

b) Giá trị phân thức $\frac{1,5-x}{5}$ nhỏ hơn giá trị phân thức $\frac{4x+5}{2}$.

Lời giải:

a) Ta có:

$\begin{array}{l}\frac{5-2x}{6}>\frac{5x-2}{3}\\ \iff \frac{5-2x}{6}.6>\frac{5x-2}{3}.6\end{array}$

⇔ 5 – 2x > 10x – 4

⇔ –2x – 10x > –4 – 5

⇔ –12x > –9⇔ $x<\frac{3}{4}$.

Vậy với $x<\frac{3}{4}$ thì giá trị phân thức $\frac{5-2x}{6}$ lớn hơn giá trị phân thức $\frac{5-2x}{3}$.

b)Ta có: $\frac{1,5-x}{5}$ < $\frac{4x+5}{2}$

$\iff \frac{1,5-x}{5}.10<\frac{4x+5}{2}.10$

⇔ 3 – 2x < 20x + 25

⇔ –2x – 20x < 25 – 3

⇔ –22x < 22⇔ x > –1

Vậy với x > –1 thì giá trị phân thức $\frac{1,5-x}{5}$ nhỏ hơn giá trị phân thức $\frac{4x+5}{2}$.

Bài 54 trang 58 SBT Toán 8 Tập 2: Hãy cho biết số nào trong các số $\frac{2}{3};\frac{2}{7};\frac{-4}{5}$ là nghiệm của bất phương trình 5 – 3x < (4 + 2x) – 1.

Lời giải:

Ta có: 5 – 3x < (4 + 2x) – 1

⇔ 5 – 3x < 4 + 2x – 1

⇔ –3x – 2x < 4 – 1 – 5

⇔ –5x < –2 ⇔ $x>\frac{2}{5}$

Vì chỉ có giá trị $\frac{2}{3}>\frac{2}{5}$ nên trong các số đã cho thì số $\frac{2}{3}$ là nghiệm của bất phương trình.

Bài 55 trang 58 SBT Toán 8 Tập 2: Hai quy tắc biến đổi tương đương của bất phương trình cũng giống như hai quy tắc biến đổi tương đương của phương trình. Điều đó có đúng không?

Lời giải:

Ta có, quy tắc chuyển vế của phương trình giống quy tắc chuyển vế của bất phương trình, nhưng quy tắc nhân hai vế của phương trình với cùng một số khác 0 không thể chuyển thành quy tắc nhân hai vế của bất phương trình với cùng một số khác 0, bởi vì bất phường trình sẽ đổi chiều khi ta nhân hai vế của nó với một số âm.

Bài 56 trang 58 SBT Toán 8 Tập 2: Cho bất phương trình ẩn x: 2x + 1 > 2(x + 1).

a) Chứng tỏ các giá trị –5; 0; –8 đều không phải là nghiệm của nó.

b) Bất phương trình này có thể nhận giá trị nào của x là nghiệm?

Lời giải:

a) Thay giá trị của x vào từng vế của bất phương trình:

+)Với x = –5 vế trái:

2.(–5) + 1 = –10 + 1 = –9

Vế phải: 2.[(–5) + 1] = 2.(–4) = –8

Vì –9 < –8 nên x = –5 không phải là nghiệm của bất phương trình.

+)Với x = 0 vế trái: 2.0 + 1 = 1

Vế phải: 2.(0 + 1) = 2

Vì 1 < 2 nên x = 0 không phải là nghiệm của bất phương trình.

+)Với x = –8 vế trái:

2.(–8) + 1 = –16 + 1 = –15

Vế phải: 2.[(–8) + 1] = 2.(–7) = –14

Vì –15 < –14 nên x = –8 không là nghiệm của bất phương trình.

b) Ta có: 2x + 1 > 2(x + 1)

      ⇔ 2x + 1 > 2x + 2

      ⇔ 0x > 1 hay 0 > 1 ( vô lí).

Vậy bất phương trình vô nghiệm.

Bài 57 trang 58 SBT Toán 8 Tập 2: Bất phương trình ẩn x:

5 + 5x < 5(x + 2)

có thể nhận những giá trị nào của ẩn x là nghiệm?

Lời giải:

Ta có: 5 + 5x < 5(x + 2)

⇔ 5 + 5x < 5x + 10

⇔ 5x – 5x < 10 – 5

⇔ 0x < 5 hay 0 < 5 (luôn đúng).

Bất kì giá trị nào của x cũng thỏa mãn vế trái nhỏ hơn vế phải.

Vậy tập nghiệm của bất phương trình là tập số thực R.

Bài 58 trang 58 SBT Toán 8 Tập 2: So sánh số a và số b nếu:

a) x < 5 ⇔ (a – b)x < 5(a – b) ;

b) x > 2 ⇔ (a – b)x < 2(a – b).

Lời giải:

a) Ta có: x < 5 ⇔ (a – b)x < 5(a – b)

⇒ a – b > 0 ⇔ a > b

b) Ta có: x > 2 ⇔ (a – b)x < 2(a – b)

⇒ a – b < 0 ⇔ a < b

Bài 59 trang 58 SBT Toán 8 Tập 2: Tìm số nguyên x lớn nhất thỏa mãn mỗi bất phương trình sau:

a) 5,2 + 0,3x < – 0,5 ;

b) 1,2 – (2,1 – 0,2x) < 4,4.

Lời giải:

a) Ta có: 5,2 + 0,3x < – 0,5

⇔ 0,3x < – 0,5 – 5,2

⇔ 0,3x < – 5,7

⇔ x < –19

Vậy số nguyên lớn nhất cần tìm là –20.

b) Ta có: 1,2 – (2,1 – 0,2x) < 4,4

⇔ 1,2 – 2,1 + 0,2x < 4,4

⇔ 0,2x < 4,4 – 1,2 + 2,1

⇔ 0,2x < 5,3

⇔ x < $\frac{53}{2}$

Vậy số nguyên lớn nhất thỏa mãn điều kiện là số 26.

Bài 60 trang 58 SBT Toán 8 Tập 2: Tìm số nguyên x bé nhất thỏa mãn mỗi bất phương trình sau:

a) 0,2x + 3,2 > 1,5

b) 4,2 – (3 – 0,4x) > 0,1x + 0,5

Lời giải:

a) Ta có: 0,2x + 3,2 > 1,5

⇔ 0,2x > 1,5 – 3,2

 ⇔ 0,2x > – 1,7

 ⇔ x > $\frac{-17}{2}$

Vậy số nguyên bé nhất cần tìm là – 8.

b) Ta có: 4,2 – (3 – 0,4x) > 0,1x + 0,5

⇔ 4,2 – 3 + 0,4x > 0,1x + 0,5

⇔ 0,4x – 0,1x > 0,5 – 4,2 + 3

⇔ 0,3x > – 0,7

⇔ x > $\frac{-7}{3}$.

Vậy số nguyên bé nhất cần tìm là –2.

Bài 61 trang 58 SBT Toán 8 Tập 2: Với giá trị nào của m thì phương trình ẩn x:

a) x – 3 = 2m + 4 có nghiệm dương?

b) 2x – 5 = m + 8 có nghiệm số âm?

Lời giải:

a) Ta có x – 3 = 2m + 4

⇔ x = 2m + 4 + 3

⇔ x = 2m + 7

Phương trình có nghiệm số dương khi

2m + 7 > 0 ⇔ $m>\frac{-7}{2}$.

b) Ta có: 2x – 5 = m + 8

⇔ 2x = m + 8 + 5

⇔ 2x = m + 13

⇔ x = $\frac{m+13}{2}$

Phương trình có nghiệm số âm khi

$\frac{m+13}{2}$ < 0 ⇔ m + 13 < 0 ⇔ m < –13.

Bài 62 trang 58 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) (x + 2)² < 2x(x + 2) + 4

b) (x + 2)(x + 4) > (x – 2)(x + 8) + 26

Lời giải:

a) Ta có: (x + 2)² < 2x(x + 2) + 4

⇔ x² + 4x + 4 < 2x² + 4x + 4

 ⇔ x² + 4x – 2x² – 4x < 4 – 4

⇔ –x² < 0

⇔ x² > 0 nên $x\ne 0$ (vì x² ≥ 0 với mọi x)

Vậy tập nghiệm của bất phương trình là:

S = {x| x ≠ 0}.

b) Ta có: (x + 2)(x + 4) > (x – 2)(x + 8) + 26

⇔ x² + 6x + 8 > x² + 6x + 10

⇔ x² + 6x – x² – 6x > 10 – 8

 ⇔ 0x > 2 (vô lý)

Vậy bất phương trình vô nghiệm.

Bài 63 trang 58 SBT Toán 8 Tập 2: Giải các bất phương trình:

a) $\frac{1-2x}{4}-2\text{\hspace{0.17em}\hspace{0.17em}}<\frac{1-5x}{8}$;

b) $\frac{x-1}{4}-1>\frac{x+1}{3}+8$.

Lời giải:

a) Ta có: $\frac{1-2x}{4}-2\text{\hspace{0.17em}\hspace{0.17em}}<\frac{1-5x}{8}$;

$\iff \frac{1-2x}{4}.8-2.8\text{\hspace{0.17em}\hspace{0.17em}}<\frac{1-5x}{8}.8$

⇔ 2 – 4x – 16 < 1 – 5x

⇔ –4x + 5x < 1 – 2 + 16

⇔ x < 15

Vậy tập nghiệm của bất phương trình là:

S = {x| x < 15}.

b) Ta có: $\frac{x-1}{4}-1>\frac{x+1}{3}+8$

$\iff \frac{x-1}{4}.12-1.12>\frac{x+1}{3}.12+8.12$

⇔ 3x – 3 – 12 > 4x + 4 + 96

⇔ 3x – 4x > 4 + 96 + 3 + 12

⇔ –x > 115 ⇔ x < –115

Vậy tập nghiệm của bất phương trình là:

S = {x| x < –115}.

Bài 64 trang 58 SBT Toán 8 Tập 2: Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau:

a) 3(5 – 4n) + (27 + 2n) > 0;

b) (n + 2)² – (n – 3)(n + 3) ≤ 40.

Lời giải:

a) Ta có: 3(5 – 4n) + (27 + 2n) > 0

⇔ 15 – 12n + 27 + 2n > 0

⇔ –10n + 42 > 0

⇔ –10n > –42

 ⇔ n < 4,2 

Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4.

b) Ta có: (n + 2)² – (n – 3)(n + 3) ≤ 40

⇔ n² + 4n + 4 – n² + 9 ≤ 40

⇔ 4n < 40 – 13

⇔ 4n < 27 $\iff n<\frac{27}{4}=6,75$.

Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4; 5; 6.

Bài tập bổ sung

Bài 4.1 trang 59 SBT Toán 8 Tập 2: Khoanh tròn vào chữ cái trước khẳng định đúng...

Bài 4.2 trang 59 SBT Toán 8 Tập 2: Khoanh tròn vào chữ cái trước hình đúng...

Bài 4.3 trang 59 SBT Toán 8 Tập 2: Với giá trị nào của m thì phương trình ẩn x...

Bài 4.4 trang 59 SBT Toán 8 Tập 2: Chứng minh hai bất phương trình sau không tương đương...

Xem thêm lời giải sách bài tập Toán học lớp 8 hay, chi tiết khác:

Bài 1: Liên hệ giữa thứ tự và phép cộng

Bài 2: Liên hệ giữa thứ tự và phép nhân

Bài 3: Bất phương trình một ẩn

Bài 5: Phương trình chứa dấu giá trị tuyệt đối

Ôn tập chương 4

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Lý thuyết Bất phương trình bậc nhất một ẩn

Trắc nghiệm Bất phương trình bậc nhất một ẩn có đáp án