Nội dung bài viết

    Xem thêm

    SBT Toán 8 Ôn tập chương 1 - Phần Đại số

    Với giải sách bài tập Toán lớp 8 Ôn tập chương 1 - Phần Đại số chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 1,326 13/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Ôn tập chương 1 - Phần Đại số

    Bài 53 trang 13 SBT Toán 8 Tập 1: Làm tính nhân:

    a) 3x(x2 – 7x + 9);

    b) 25xy(x2y – 5x + 10y) .

    Lời giải:

    a) 3x(x2 – 7x + 9)

    = 3x.x2 + 3x.(– 7x) + 3x.9

    = 3x3 – 21x2 + 27x

    b) 25xy(x2y – 5x + 10y)

    = 25.xy .x2y + 25.xy. (– 5x) + 25xy.10y

    = 25x3y2 – 2x2y + 4xy2

    Bài 54 trang 14 SBT Toán 8 Tập 1: Làm tính nhân:

    a) (x2 – 1)(x2 + 2x) ;

    b) (x + 3y)(x2 – 2xy + y) ;

    c) (2x – 1)(3x + 2)(3 – x).

    Lời giải:

    a) (x2 – 1)(x2 + 2x)

    = x2.(x2 + 2x) – 1.(x2 + 2x)

    = x4 + 2x3 – x2 – 2x

    b) (x + 3y)(x2 – 2xy + y)

    = x. (x2 – 2xy + y) + 3y.(x2 – 2xy + y)

    = x3 – 2x2y + xy + 3x2y – 6xy2 + 3y2

    = x3 + (3x2y – 2x2y) + xy – 6xy2 + 3y2

    = x3 + x2y + xy – 6xy2 + 3y2

    c) (2x – 1)(3x + 2)(3 – x)

    = [2x.(3x + 2) – 1.(3x + 2)] . (3 – x)

    = (6x2 + 4x – 3x – 2)(3 – x)

    = (6x2 + x – 2)(3 – x)

    = 6x2.(3 – x) + x(3 – x) – 2(3 – x)

    = 18x2 – 6x3 + 3x – x2 – 6 + 2x

    = (18x2 – x2) – 6x3 + (3x + 2x) – 6

    = 17x2 – 6x3 + 5x – 6

    Bài 55 trang 14 SBT Toán 8 Tập 1: Tính nhanh giá trị của mỗi biểu thức sau:

    a) 1,62 + 4.0,8.3,4 + 3,42 ;

    b) 34.54 – (152 + 1)(152 – 1);

    c) x4 – 12x3 + 12x2 – 12x + 111 tại x = 11.

    Lời giải:

    a) 1,62 + 4.0,8.3,4 + 3,42

    = 1,62 + 2.1,6.3,4 + 3,42 ( vì 4.0,8 = 2.2.0,8 = 2.1,6)

    = (1,6 + 3,4)2 

    = 52 = 25

    b) 34.54 – (152 + 1)(152 – 1)

    = (3.5)4 – [(152)2 – 12]

    = (3.5)4 – (154 – 1)

    = 154 – 154 + 1

    = 1

    c) Với x = 11, ta có: 12 = 11 + 1 = x + 1

    Suy ra: x4 – 12x3 + 12x2 – 12x + 111

    = x4 – (x + 1)x3 + (x + 1)x2 – (x + 1)x + 111

    = x4 – x4 – x3 + x3 + x2 – x2 – x + 111

    = (x4 – x4 ) + (x3 – x3) + (x2 – x2 ) – x + 111

    = – x + 111

    Thay x = 11 vào biểu thức ta được: – x + 111 = – 11 + 111 = 100                                       

    Vậy giá trị của biểu thức tại x = 11 là 100.

    Bài 56 trang 14 SBT Toán 8 Tập 1: Rút gọn biểu thức:

    a) (6x + 1)2 + (6x – 1)2 – 2(1 + 6x)(6x – 1);

    b) 3(22 + 1)(24 + 1)(28 + 1)(216 + 1).

    Lời giải:

    a) (6x + 1)2 + (6x – 1)2 – 2(1 + 6x)(6x – 1)

    = (6x + 1)2 – 2(1 + 6x)(6x – 1) + (6x – 1)2

    = [(6x + 1) – (6x – 1)]2

    = (6x + 1 – 6x + 1)2 

    = 22 = 4

    b) 3(22 + 1)(24 + 1)(28 + 1)(216 + 1)

    = (22 – 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)

     (vì 22 – 1 = 4 – 1= 3)

    = ((22)2 – 1)(24 + 1)(28 + 1)(216 + 1)

    = (24 – 1)(24 + 1)(28 + 1)(216 + 1)

    = (28 – 1)(28 + 1)(216 + 1)

    = (216 – 1)(216 + 1)

    = 232 – 1

    Bài 57 trang 14 SBT Toán 8 Tập 1: Phân tích đa thức thành nhân tử:

    a) x3 – 3x2 – 4x + 12;

    b) x4 – 5x2 + 4;

    c) (x + y + z)3 – x3 – y3 – z3 .

    Lời giải:

    a) x3 – 3x2 – 4x + 12

    = (x3 – 3x2 ) – (4x – 12)

    = x2(x – 3) – 4(x – 3)

    = (x – 3)(x2 – 4)

    = (x – 3)(x + 2)(x – 2)

    b) x4 – 5x2 + 4

    = x4 – 4x2 – x2 + 4

    = (x4 – 4x2 ) – (x2 – 4)

    = x2(x2 – 4) – 1.(x2 – 4)

    = (x2 – 4)( x2 – 1)

    = (x + 2)(x – 2)(x + 1)(x – 1)

    c) (x + y + z)3 – x3 – y3 – z3

    = [(x + y) + z]3 – x3 – y3 – z3

    = (x + y)3 + 3(x + y)2z + 3(x + y)z2 + z3 – x3 – y3 – z3

    = x3 + y3 + 3xy(x + y) + 3(x + y)2z + 3(x + y)z2 – x3 – y3

      (vì z3 – z3 = 0 ; 3x2y + 3xy2 = 3xy (x + y)).

    = 3xy.(x + y) + 3(x + y)2.z + 3(x + y).z2

    = 3(x + y)[xy + (x + y)z + z2]

    = 3(x + y)[xy + xz + yz + z2]

    = 3(x + y)[x(y + z) + z(y + z)]

    = 3(x + y)(y + z)(x + z).

    Bài 58 trang 14 SBT Toán 8 Tập 1: Làm tính chia:

    a) (2x3 + 5x2 – 2x + 3) : (2x2 – x + 1);

    b) (2x3 – 5x2 + 6x – 15) : (2x – 5);

    c) (x4 – x – 14) : (x – 2).

    Lời giải:

    a)

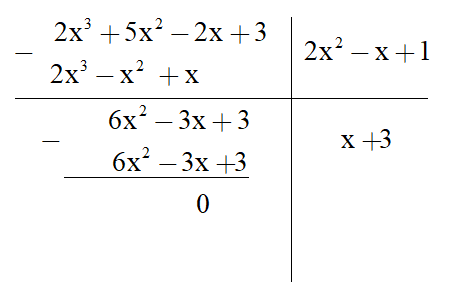
    Tài liệu VietJack

    Vậy (2x3 + 5x2 – 2x + 3) : (2x2 – x + 1) = x + 3

    b)

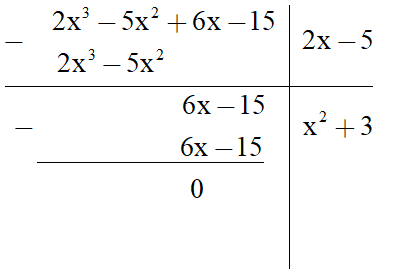
    Tài liệu VietJack

    Vậy (2x3 – 5x2 + 6x – 15) : (2x – 5) = x2 + 3.

    c)

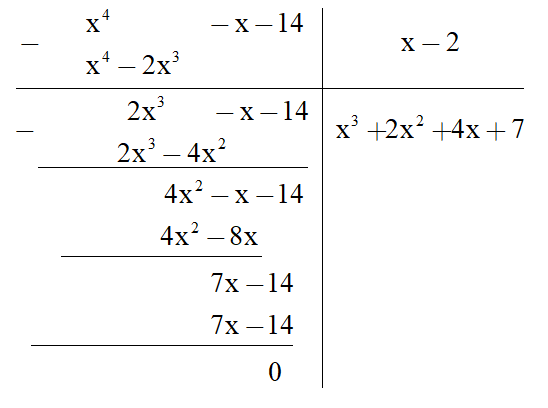
    Tài liệu VietJack

    Vậy (x4 – x – 14) : (x – 2) = x3 + 2x2 + 4x + 7.

    Bài 59 trang 14 SBT Toán 8 Tập 1: Tìm giá trị lớn nhất (hoặc nhỏ nhất) của các biểu thức sau:

    a) A = x2 – 6x + 11;

    b) B = 2x2 + 10x – 1;

    c) C = 5x – x2.

    Lời giải:

    a) Ta có: A = x2 – 6x + 11

    = x2 – 2.3x + 9 + 2

    = (x – 3)2 + 2

    Vì (x – 3)2 ≥ 0 với mọi x nên (x – 3)2 + 2 ≥ 2

    Suy ra: A ≥ 2.

    A = 2 khi và chỉ khi x – 3 = 0 hay x = 3.

    Vậy A = 2 là giá trị nhỏ nhất của biểu thức tại x = 3.

    b) B = 2x2 + 10x – 1

    = 2(x2 + 5x – 12)

    = 2[x2 + 2. 52x + (52 )2 – (52 )2 – 12 ]

    = 2[(x + )2 – 254 – 24 ]

    = 2[(x + 52)2 –  274] = 2(x + 52)2 – 272

    Vì (x + 52)2 ≥ 0 với mọi x nên 2(x + 52)2 ≥ 0

     2(x + )2 –  272≥ -272

    Suy ra: B ≥-272 .

    B = −272 khi và chỉ khi x + 52 = 0 suy ra x = – 52

    Vậy B = -272 là giá trị nhỏ nhất của biểu thức tại x = – 52.

    c) C = 5x – x2 = – (x2 – 5x)

    = – [x2 – 2. 52x + (52 )2 – (52 )2]

    = – [(x – 52)2 – 254] = – (x – 52)2 + 254

    Vì – (x – 52)2 ≤ 0 với mọi x nên – (x – 52)2 + 254≤254

    Suy ra: C ≤254.

    C = 254 khi và chỉ khi x - 52 = 0 suy ra x = 52.

    Vậy C = 254 là giá trị lớn nhất của biểu thức tại x = 52 .

    Bài tập bổ sung

    Bài I.1 trang 14 SBT Toán 8 Tập 1: Kết quả của phép tính (x + 2)(x − 1)...

    Bài I.2 trang 14 SBT Toán 8 Tập 1: Rút gọn biểu thức x(x − y) − y(y − x) ta được...

    Bài I.3 trang 14 SBT Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử...

    Bài I.4 trang 15 SBT Toán 8 Tập 1: Làm tính chia (2x5 − 5x3 + x2 + 3x − 1) : (x2 − 1)...

    Bài I.5 trang 15 SBT Toán 8 Tập 1: Tính giá trị lớn nhất hoặc nhỏ nhất của các biểu thức...

    Xem thêm lời giải sách bài tập Toán học lớp 8 hay, chi tiết khác:

    Bài 1: Phân thức đại số

    Bài 2: Tính chất cơ bản của phân thức

    Bài 3: Rút gọn phân thức

    Bài 4: Quy đồng mẫu thức nhiều phân thức

    Bài 5: Phép cộng các phân thức đại số

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Ôn tập chương 1

    Trắc nghiệm Bài tập ôn tập chương 1 có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,326 13/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: