SBT Toán 8 Bài 3: Hình thang cân

Mục lục Giải SBT Toán 8 Bài 3: Hình thang cân

Bài 22 trang 82 SBT Toán 8 Tập 1: Hình thang cân ABCD có AB // CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng: DH = CK.

Lời giải:

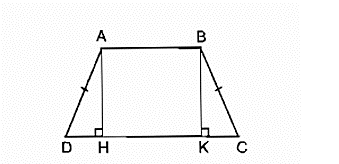
Xét hai tam giác vuông AHD và BKC:

$\widehat{AHD}=\widehat{BKC}$ = 90^o

AD = BC (tính chất hình thang cân)

$\widehat{C}=\widehat{D}$ (tính chất hình thang cân)

Do đó, ΔAHD = ΔBKC (cạnh huyền - góc nhọn)

⇒ HD = KC  (điều phải chứng minh).

Bài 23 trang 82 SBT Toán 8 Tập 1: Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD.

Lời giải:

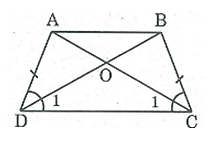
Xét ΔADC và ΔBCD, ta có:

AD = BC (tính chất hình thang cân)

$\widehat{ADC}=\widehat{BCD}$ (hai góc kề một đáy)

DC chung

Do đó: ΔADC = ΔBCD (c.g.c)

⇒ $\widehat{C_1}=\widehat{D_1}$

Trong ΔOCD ta có: $\widehat{C_1}=\widehat{D_1}$

 ⇒ ΔOCD cân tại O

⇒ OC = OD (1)

Mà AC = BD (tính chất hình thang cân)

Do đó: AO + OC = BO + OD (2)

Từ (1) và (2) suy ra: AO = BO (điều phải chứng minh).

Bài 24 trang 83 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy các điểm M, N sao cho BM = CN.

a) Tứ giác BMNC là hình gì? Vì sao?

b) Tính các góc của tứ giác BMNC biết rằng góc $\hat{A}$ = 40^o

Lời giải:

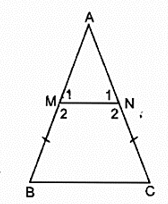
a) ΔABC cân tại A

⇒ $\widehat{B}=\widehat{C}$  (tính chất tam giác cân)

Mà $\widehat{A}+\text{\hspace{0.17em}}\widehat{B}+\text{}\widehat{C}={180}^0$ nên $\widehat{B}=\widehat{C}=\frac{{180}^0-\widehat{A}}{2}$ (1)

Vì AB = AC (giả thiết)

⇒ AM + BM = AN + CN

Mà BM = CN (giả thiết)

⇒ AM = AN

⇒ ΔAMN cân tại A.

⇒ $\widehat{M_1}=\widehat{N_1}$ = $\frac{{180}^0-\widehat{A}}{2}$ (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: $\widehat{M_1}=\widehat{B}$

⇒ MN // BC (vì có cặp góc đồng vị bằng nhau).

Tứ giác BCNM là hình thang có $\widehat{B}=\widehat{C}$

Vậy BCNM là hình thang cân.

b) $\widehat{B}=\widehat{C}$ = $\frac{{180}^0-\widehat{A}}{2}$

$=\frac{{180}^0-{40}^0}{2}={70}^0$

Mà $\widehat{M_2}+\widehat{B}$ = 180^o (hai góc trong cùng phía nên bù nhau)

Suy ra: $\widehat{M_2}$ = 180^o - $\widehat{B}$

 = 180^o – 70^o = 110^o

$\widehat{N_2}=\widehat{M_2}$ = 110^o (tính chất hình thang cân).

Bài 25 trang 83 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.

Lời giải:

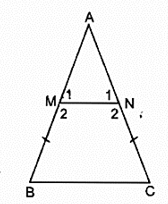
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:

$\begin{array}{l}\widehat{ABE}=\frac{1}{2}\widehat{B};\\ \widehat{ACF}=\frac{1}{2}\widehat{C}\end{array}$

Mà tam giác ABC cân tại A nên $\widehat{B}=\widehat{C}$

Suy ra: $\widehat{ABE}=\widehat{ACF}$

Xét hai tam giác AEB và AFC

Có AB = AC (ΔABC cân tại A)

$\widehat{ABE}=\widehat{ACF}$ (chứng minh trên)

$\widehat{A}$ là góc chung

⇒ ΔAEB = ΔAFC (g.c.g)

⇒ AE = AF ⇒ ΔAEF cân tại A

⇒ $\widehat{A\text{}FE}=\frac{{180}^0-\widehat{A}}{2}$

Vì tam giác ABC cân tại A nên $\widehat{B}=\frac{{180}^0-\widehat{A}}{2}$ (tính chất).

⇒ $\widehat{AFE}=\widehat{B}$ 

⇒ FE // BC (có hai góc ở vị trí đồng vị bằng nhau).

⇒ Tứ giác BFEC là hình thang.

Lại có: $\widehat{B}=\widehat{C}$(tính chất tam giác cân)

Do đó hình thang BFEC là hình thang cân

Vì FE // BC nên ta có: $\widehat{FEB}=\widehat{EBC}$ (so le trong)

Lại có: $\widehat{FBE}=\widehat{EBC}$ ( vì BE là tia phân giác của góc B)

⇒ $\widehat{FBE}=\widehat{FEB}$

⇒ ΔFBE cân ở F ⇒ FB = FE

⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm).

Bài 26 trang 83 SBT Toán 8 Tập 1: Chứng minh hình thang có hai đường chéo bằng nhau là hình thang cân.

Lời giải:

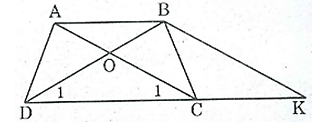
Giả sử ta có hình thang ABCD, AB // CD và AC = BD. Ta đi chứng min ABCD là hình thang cân

Từ B kẻ đường thẳng song song với AC cắt đường thẳng DC tại K.

Ta có hình thang ABKC có hai cạnh bên BK // AC nên AC = BK

Mà AC = BD (giả thiết)

Suy ra: BD = BK do đó ΔBDK cân tại B

⇒ $\widehat{D_1}=\widehat{K}$ (tính chất hai tam giác cân)

Ta lại có: $\widehat{C_1}=\widehat{K}$(hai góc đồng vị)

Suy ra: $\widehat{D_1}=\widehat{C_1}$

Xét ΔACD và ΔBDC:

AC = BD (giả thiết)

$\widehat{C_1}=\widehat{D_1}$ (chứng minh trên)

CD chung

Do đó ΔACD = ΔBDC (c.g.c)

⇒$\widehat{ADC}$ = $\widehat{BCD}$ (hai góc tương ứng)

Hình thang ABCD có $\widehat{ADC}=\widehat{BCD}$ nên là hình thang cân.

Bài 27 trang 83 SBT Toán 8 Tập 1: Tính các góc của hình thang cân, biết một góc bằng 50^o

Lời giải:

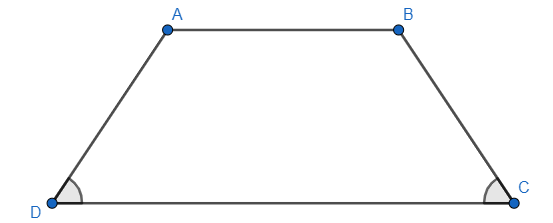
Giả sử hình thang ABCD có AB // CD và $\widehat{D}$ = 50^o

Vì $\widehat{C}=\widehat{D}$ (tính chất hình thang cân)

⇒$\widehat{C}$ = 50^o

Lại có: $\widehat{A}+\text{\hspace{0.17em}}\widehat{D}$ = 180^o (hai góc trong cùng phía)

⇒$\widehat{A}$ = 180^o - $\widehat{D}$ 

= 180^o – 50^o = 130^o

Mà $\widehat{B}=\widehat{A}$ (tính chất hình thang cân)

Suy ra: $\widehat{B}$ = 130^o.

Bài 28 trang 83 SBT Toán 8 Tập 1: Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.

Lời giải:

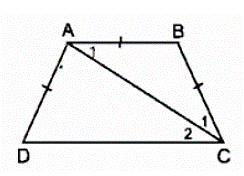
Ta có:

AB = AD (giả thiết)

AD = BC (tính chất hình thang cân)

⇒ AB = BC do đó ΔABC cân tại B

⇒ $\widehat{BAC}=\widehat{BCA}$ (tính chất tam giác cân) (*)

Vì ABCD là hình thang có đáy là AB nên AB // CD

$\widehat{BAC}=\widehat{DCA}$ (hai góc so le trong) (**)

Từ (*) và (**) suy ra: $\widehat{BCA}=\widehat{DCA}$ (cùng bằng )

Vậy CA là tia phân giác của $\widehat{BCD}$

Bài 29 trang 83 SBT Toán 8 Tập 1: Hai đoạn thẳng AB và CD cắt nhau tại O. Biết rằng OA = OC, OB = OD. Tứ giác ABCD là hình gì ? Vì sao

Lời giải:

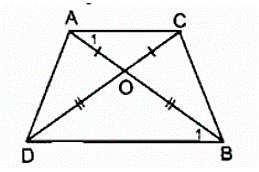
Ta có: OA = OC (giả thiết)

⇒ ΔOAC cân tại O

⇒ $\widehat{A_1}=\frac{{180}^0-\widehat{AOC}}{2}$ (tính chất tam giác cân) (1)

OB = OD (giả thiết)

⇒ ΔOBD cân tại O.

⇒ $\widehat{B_1}=\frac{{180}^0-\widehat{BOD}}{2}$ (tính chất tam giác cân) (2)

Mà $\widehat{AOC}=\widehat{BOD}$ (đối đỉnh) (3)

Từ (1), (2), (3) suy ra: $\hat{A}=\widehat{B_1}$

⇒ AC // BD (vì có cặp góc ở vị trí so le trong bằng nhau)

Suy ra: Tứ giác ACBD là hình thang.

Ta có: AB = OA + OB

Và CD = OC + OD

Mà OA = OC, OB = OD

Suy ra: AB = CD.

Vậy hình thang ABCD là hình thang cân.

Bài 30 trang 83 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.

a) Tứ giác BDEC là hình gì? Vì sao

b) Các điểm D, E ở vị trí nào thì BD = DE = EC?

Lời giải:

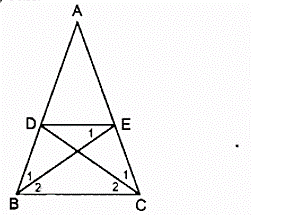
a) Vì AD = AE

⇒ ΔADE cân tại A nên $\widehat{ADE}=\frac{{180}^0-\widehat{A}}{2}$ (tính chất tam giác cân)

ΔABC cân tại A

⇒ $\widehat{ABC}=\frac{{180}^0-\widehat{A}}{2}$ (tính chất tam giác cân)

Suy ra: $\widehat{ADE}=\widehat{ABC}$ mà hai góc này ở vị trí đồng vị

⇒ DE // BC (có cặp góc đồng vị bằng nhau)

Do đó, tứ giác BDEC là hình thang.

Lại có: $\widehat{ABC}=\widehat{ACB}$ (tính chất tam giác cân) hay $\widehat{DBC}=\widehat{ECB}$

Vậy BDEC là hình thang cân.

b) Ta có: BD = DE

⇒ ΔBDE cân tại D

Suy ra: $\widehat{B_1}=\widehat{E_1}$

Mà $\widehat{E_1}=\widehat{B_2}$ (so le trong)

⇒ $\widehat{B_1}=\widehat{B_2}$

DE = EC ⇒ ΔDEC cân tại E

⇒ $\widehat{CDE}=\widehat{C_1}$

$\widehat{CDE}=\widehat{C_2}$(so le trong)

⇒ $\widehat{C_1}=\widehat{C_2}$

Vậy khi BE là tia phân giác của $\widehat{ABC}$ , CD là tia phân giác của $\widehat{ACB}$thì BD = DE = EC.

Bài 31 trang 83 SBT Toán 8 Tập 1: Hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.

Lời giải:

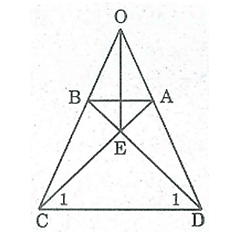
Ta có: $\widehat{ADC}=\widehat{BCD}$ (do ABCD là hình thang cân)

⇒ $\widehat{ODC}=\widehat{OCD}$

⇒ΔOCD cân tại O

Suy ra:  OC = OD

Hay OB + BC = OA + AD

Mà AD = BC (tính chất hình thang cân)

⇒ OA = OB

Xét ΔADC và ΔBCD:

AD = BC (tính chất hình thang cân )

AC = BD (tính chất hình thang cân)

CD chung

Do đó ΔADC = ΔBCD (c.c.c)

⇒ $\widehat{D_1}=\widehat{C_1}$

⇒ΔEDC cân tại E

⇒ EC = ED nên E thuộc đường trung trực CD

OC = OD nên O thuộc đường trung trực CD

Mà E ≠ O nên OE là đường trung trực của CD.

Ta có: BD= AC (tính chất hình thang cân)

⇒ EB + ED = EA + EC mà ED = EC

⇒ EB = EA nên E thuộc đường trung trực AB

OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB

Mà E ≠ O nên OE là đường trung trực của AB.

Bài 32 trang 83 SBT Toán 8 Tập 1:

a) Hình thang ABCD có đáy nhỏ AB = b , đáy lớn CD = a, đường cao AH. Chứng minh rằng $HD\text{\hspace{0.17em}\hspace{0.17em}}=\frac{a-b}{2};\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}HC\text{}=\frac{a+\text{\hspace{0.17em}\hspace{0.17em}}b}{2}$(a, b có cùng đơn vị đo).

b) Tính đường cao của hình thang cân có hai đáy 10cm, 26cm và cạnh bên 17cm.

Lời giải:

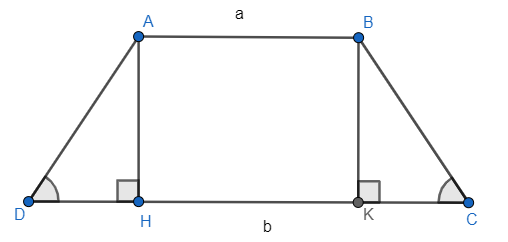
a) Kẻ đường cao BK

Xét hai tam giác vuông AHD và BKC, ta có:

$\widehat{AHD}=\widehat{BKC}$ = 90^o

AD = BC (tính chất hình thang cân)

$\widehat{D}=\widehat{C}$ (ABCD là hình thang cân)

Do đó: ΔAHD = ΔBKC (cạnh huyền, góc nhọn)

⇒ HD = KC.

Hình thang ABKH có hai cạnh bên song song nên AB = HK

a – b = DC – AB = DC – HK

= HD + KC = 2HD

Suy ra: $HD\text{\hspace{0.17em}\hspace{0.17em}}=\frac{a-b}{2}$

$HC=DC-HD$

$\text{\hspace{0.17em}\hspace{0.17em}}=a-\frac{a-b}{2}=\frac{a+b}{2}$ ( điều phải chứng minh).

b) Áp dụng kết quả ý a:

Ta có: 

$\begin{array}{l}HD\text{\hspace{0.17em}}=\frac{CD\text{\hspace{0.17em}\hspace{0.17em}}-AB}{2}\\ =\frac{26-10}{2}=8cm\end{array}$

Trong tam giác vuông AHD có $\widehat{AHD}$ = 90^o

AD² = AH² + HD² (định lý Py-ta-go)

⇒ AH² = AD² - HD²

AH² = l7² - 8²= 289 – 64 = 225

AH = 15 (cm).

Bài 33 trang 83 SBT Toán 8 Tập 1: Hình thang cân ABCD có đường chéo BD vuông góc với cạnh bên BC, BD là tia phân giác của góc D. Tính chu vi của hình thang, biết BC = 3cm.

Lời giải:

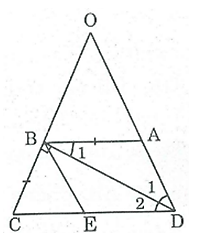
Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)

$\widehat{ABD}\text{\hspace{0.17em}}=\widehat{BDC}$(so le trong)

$\widehat{ADB}\text{\hspace{0.17em}}=\widehat{BDC}$ (do DB là tia phân giác của góc D )

⇒ $\widehat{ABD}\text{\hspace{0.17em}}=\widehat{ADB}$

Suy ra: ΔABD cân tại A.

⇒ AB = AD = 3 (cm)

Vì ΔBDC vuông tại B nên $\widehat{BDC}+\widehat{C}$ = 90^o

Mà $\widehat{ADC}=\widehat{C}$ (do ABCD là hình thang cân) và $\widehat{BDC}=\frac{1}{2}\widehat{ADC}$

Suy ra: $\widehat{BDC}=\frac{1}{2}\widehat{C}$

Khi đó; $\widehat{C}+\frac{1}{2}\widehat{C}={90}^0$

$\hspace{0.17em}\Rightarrow \widehat{C}={60}^0$

Từ B kẻ đường thẳng song song AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

Mà $\widehat{BEC}=\widehat{ADC}$ (đồng vị)

Suy ra: $\widehat{BEC}=\widehat{C}$

⇒ΔBEC cân tại B có $\widehat{C}$ = 60^o

Suy ra: ΔBEC đều

⇒ EC = BC = 3 (cm)

Ta có: CD = CE + ED

= 3 + 3 = 6(cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA

= 3 + 3 + 6 + 3 = 15 (cm)

Bài tập bổ sung

Bài 3.1 trang 83 SBT Toán 8 Tập 1: Hình thang cân ABCD (AB// CD) có = 70^o. Khẳng định nào dưới đây là đúng?...

Bài 3.2 trang 84 SBT Toán 8 Tập 1: Hình thang cân ABCD (AB// CD) có hai đường chéo cắt nhau tại I, hai đường thẳng chứa các cạnh...

Bài 3.3 trang 84 SBT Toán 8 Tập 1: Hình thang cân ABCD (AB // CD) có , DB là tia phân giác của góc D. Tính các cạnh của hình thang...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 4: Đường trung bình của tam giác, của hình thang

Bài 5: Dựng hình bằng thước và compa. Dựng hình thang

Bài 6: Đối xứng trục

Bài 7: Hình bình hành

Bài 8: Đối xứng tâm

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Hình thang cân có đáp án