Nội dung bài viết

    Xem thêm

    SBT Toán 8 Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)

    Với giải sách bài tập Toán lớp 8 Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c) chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

    1 1,375 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 8 Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)

    Bài 29 trang 90 SBT Toán 8 Tập 2: Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không?

    a) 4cm; 5cm; 6cm và 8mm; 10mm; 12mm.

    b) 3cm; 4cm; 6cm và 9cm; 15cm; 18cm.

    c) 1dm; 2dm; 2dm và 1dm; 1dm; 0,5dm

    Lời giải:

    a) 4 cm = 40 mm; 5 cm = 50 mm, 6 cm = 60 mm

    Ta có: 408 =  5010  =  6012  =  5.Vậy hai tam giác đó đồng dạng.

    b) Ta có: 39  =  13; 618  =  13 

    Nhưng 13 ≠415  ⇒39 =  618  ≠415.

     Vậy hai tam giác đó không đồng dạng.

    c) Ta có: 12  =  12  =  0,51.

     Vậy hai tam giác đó đồng dạng.

    Bài 30 trang 90 SBT Toán 8 Tập 2: Tam giác vuông ABC ( A^ = 90o) có AB = 6cm, AC = 8cm và tam giác vuông A’B’C’ ( A'^ = 90o) có A’B’ = 9cm, B’C’ = 15cm. Hỏi rằng hai tam giác vuông ABC và A’B’C’ có đồng dạng với nhau không? Vì sao?

    Lời giải:

    * Trong tam giác vuông A’B’C’ có A'^ = 90o

    Áp dụng định lí Pi-ta-go, ta có: A’B’2 + A’C’2 = B’C’2

    Suy ra: A’C’2 = B’C’2 - A’B’2 = 152 - 92 = 144

    Suy ra: A’C’ = 12 (cm)

    * Trong tam giác vuông ABC có A^ = 90o

    Áp dụng định lí Pi-ta-go, ta có: BC2 = AB2 + AC2 = 62 + 82 =100

    Suy ra: BC = 10 (cm)

    Ta có:

    A'B'AB  = 96  = 32;A'C'AC  =  128  = 32;B'C'BC  =  1510  = 32

    Suy ra: A'B'AB  = A'C'AC  =  B'C'BC =  32

    Vậy ΔA’B’C’ đồng dạng ΔABC (c.c.c).

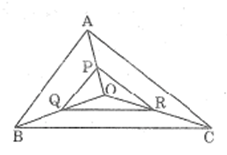
    Bài 31 trang 90 SBT Toán 8 Tập 2: Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P, Q, R theo thứ tự là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.

    Tài liệu VietJack

    Lời giải:

    Trong ΔOAB, ta có PQ là đường trung bình nên: PQ = 12AB (tính chất đường trung bình của tam giác)

    Suy ra: PQAB =  12 (1)

    Trong ΔOAC, ta có PR là đường trung bình nên:

    PR = 12AC (tính chất đường trung bình của tam giác)

    Suy ra: PRAC  =  12 (2)

    Trong ΔOBC, ta có QR là đường trung bình nên

    QR = 12 BC (tính chất đường trung bình của tam giác)

    Suy ra: QRBC  =  12  (3)

    Từ (1), (2) và (3) suy ra: PQAB  =  PRAC  =  QRBC .

    Vậy ΔPQR đồng dạng ΔABC (c.c.c).

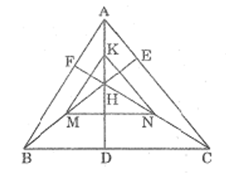
    Bài 32 trang 91 SBT Toán 8 Tập 2: Tam giác ABC có ba góc nhọn và có trực tâm là điểm H. Gọi K, M, N thứ tự là trung điểm của các đoạn thẳng AH, BH, CH. Chứng minh rằng tam giác KMN đồng dạng với tam giác ABC với tỉ số đồng dạng k = 12.

    Tài liệu VietJack

    Lời giải:

    * Trong ΔAHB, ta có:

    K trung điểm của AH (gt)

    M trung điểm của BH (gt)

    Suy ra KM là đường trung bình của tam giác AHB.

    Suy ra: KM = 12AB (tính chất đường trung bình của tam giác)

    Suy ra: KMAB  =  12  (1)

    * Trong ΔAHC, ta có:

    K trung điểm của AH (gt)

    N trung điểm của CH (gt)

    Suy ra KN là đường trung bình của tam giác AHC.

    Suy ra: KN = 12AC (tính chất đường trung bình của tam giác)

    Suy ra: KNAC  =  12  (2)

    * Trong ΔBHC, ta có:

    M trung điểm của BH (gt)

    N trung điểm của CH (gt)

    Suy ra MN là đường trung bình của tam giác BHC.

    Suy ra: MN = 12 BC (tính chất đường trung bình của tam giác)

    Suy ra: MNBC  = 12 (3)

    Từ (1), (2) và (3) suy ra: KMAB  =  KNAC  =  MNBC  =  12

    Vậy ΔKMN đồng dạng ΔABC (c.c.c)

    Tỉ số đồng dạng: k=  KMAB  =  12 .

    Bài 33 trang 91 SBT Toán 8 Tập 2: Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.

    a) Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.

    b) Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543 cm.

    Lời giải:

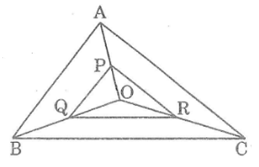
    Tài liệu VietJack

    a) * Trong ΔAOB ta có:

    P trung điểm của OA (gt)

    Q trung điểm của OB (gt)

    Suy ra PQ là đường trung bình của ΔAOB

    Suy ra: PQ = 12AB (tính chất đường trung bình của tam giác)

    Suy ra: PQAB  =  12  (1)

    * Trong ΔOAC, ta có:

    P trung điểm của OA (gt)

    R trung điểm của OC (gt)

    Suy ra PR là đường trung bình của tam giác OAC.

    Suy ra: PR = 12AC (tính chất đường trung bình của tam giác)

    Suy ra: PRAC  = 12  (2)

    * Trong ΔOBC, ta có:

    Q trung điểm của OB (gt)

    R trung điểm của OC (gt)

    Suy ra QR là đường trung bình của tam giác OBC

    Suy ra: QR = 12BC (tính chất đường trung bình của tam giác)

    Suy ra: QRBC = 12  (3)

    Từ (1), (2) và (3) suy ra: PQAB  =  PRAC =QRBC = 12

    Vậy ΔPQR đồng dạng ΔABC (c.c.c).

    b) Gọi p’ là chu vi tam giác PQR.

    Theo a ta có: PQAB  =  PRAC =QRBC = 12  (4)

    Theo tính chất của dãy tỉ số bằng nhau:

    PQAB  =  PRAC =QRBC = PQ+​ PR+​ QRAB+​​AC+​ BC = p'p  (5)

    Từ (4); (5) suy ra:

    p'p  =  12  ⇒p'= 12p= 12.543= 271,5​​(cm)

    Bài 34 trang 91 SBT Toán 8 Tập 2: Cho tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k=  23.

    Lời giải:

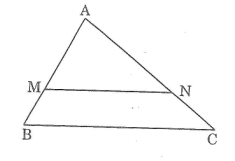
    Tài liệu VietJack

    * Cách dựng:

    - Trên cạnh AB dựng điểm M sao cho AM = 23AB

    - Trên cạnh AC dựng điểm N sao cho AN = 23AC

    - Dựng đoạn thẳng MN ta được tam giác AMN đồng dạng với tam giác ABC theo tỉ số đồng dạng k=  23.

    * Chứng minh:

    Theo cách dựng ta có:

    AM = 23AB ⇒AMAB  =  23

    AN = 23AC ⇒ANAC  =  23

    Suy ra: AMAB  =  ANAC .

    Trong ΔABC, ta có: AMAB  =  ANAC

    Theo định lí đảo của định lí Ta-lét ta có: MN // BC

    Vậy ΔAMN đồng dạng ΔABC và k=  AMAB  =  23 .

    Bài tập bổ sung

    Bài 5.1 trang 91 SBT Toán 8 Tập 2: Hai tam giác mà các cạnh có độ dài sau đây thì đồng dạng với nhau. Trường hợp nào đúng ? Trường hợp nào sai ?...

    Bài 5.2 trang 91 SBT Toán 8 Tập 2: Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó...

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 6: Trường hợp đồng dạng thứ hai (c.g.c)

    Bài 7: Trường hợp đồng dạng thứ ba (g.g)

    Bài 8: Các trường hợp đồng dạng của tam giác vuông

    Ôn tập chương 3 - Hình học

    Bài 1: Hình hộp chữ nhật

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Lý thuyết Trường hợp đồng dạng thứ nhất

    Trắc nghiệm Trường hợp đồng dạng thứ nhất của tam giác có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,375 19/09/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: