SBT Toán 8 Bài 7: Hình bình hành

Mục lục Giải SBT Toán 8 Bài 7: Hình bình hành

Bài 75 trang 89 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.

Lời giải:

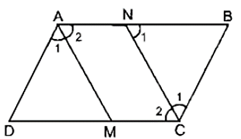
Vì ABCD là hình bình hàn nên ta có:

$\widehat{A}=\widehat{C}$ (tính chất hình bình hành)

$\widehat{A_2}=\frac{1}{2}\widehat{A}$ (Vì AM là tia phân giác của )

$\widehat{C_2}=\frac{1}{2}\widehat{C}$ ( Vì CN là tia phân giác của )

Suy ra: $\widehat{A_2}=\widehat{C_2}$.

Do ABCD là hình bình hành nên AB // CD (tính chất hình bình hành).

Hay AN // CM (1)

Mà $\widehat{N_1}=\widehat{C_2}$ (so le trong) và $\widehat{A_2}=\widehat{C_2}$

Suy ra: $\widehat{A_2}=\widehat{N_1}$.

⇒ AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)

Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.

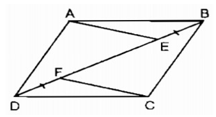
Bài 76 trang 89 SBT Toán 8 Tập 1: Trên hình 8, cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.

Lời giải:

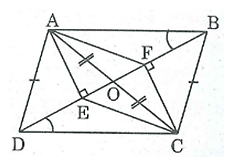
Gọi O là giao điểm của AC và BD, ta có:

OA = OC (tính chất hình bình hành) (1)

Xét hai tam giác vuông AEO và CFO, ta có:

$\widehat{AEO}=\widehat{CFO}$ = 90^o

OA = OC (chứng minh trên)

$\widehat{AOE}=\widehat{COF}$ (đối đỉnh)

Do đó ΔAEO = ΔCFO (cạnh huyền - góc nhọn).

⇒ OE = OF. Hay O là trung điểm của EF (2)

Từ (1) và (2) suy ra tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

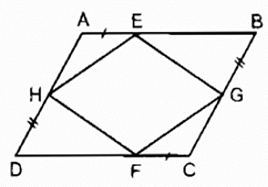
Bài 77 trang 89 SBT Toán 8 Tập 1: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

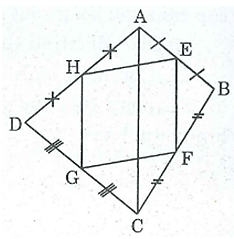
Nối đường chéo AC.

Trong ΔABC ta có:

E là trung điểm của AB (giả thiết)

F là trung điểm của BC (giả thiết)

Nên EF là đường trung bình của ΔABC

⇒EF//AC và EF = $\frac{1}{2}$AC (tính chất đường trung hình tam giác) (1)

Trong ΔADC ta có:

H là trung điểm của AD (giả thiết)

G là trung điểm của DC (giả thiết)

Nên HG là đường trung bình của ΔADC.

⇒ HG // AC và HG = $\frac{1}{2}$AC (tính chất đường trung bình tam giác) (2)

Từ (1) và (2) suy ra:

EF // HG và EF = HG.

Vậy tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Bài 78 trang 89 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chứng minh rằng DE = EF = FB.

Lời giải:

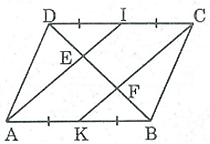
Ta có: AB = CD (tính chất hình bình hành).

Vì I, K theo thứ tự là trung điểm của CD, AB nên $AK=\frac{1}{2}\text{}AB;CI=\frac{1}{2}CD\text{}$

Suy ra: AK = CI (1)

Mặt khác: AB // CD (vì ABCD là hình bình hành).

⇒ AK // CI (2).

Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

⇒ AI // CK.

Trong ΔABE, ta có:

K là trung điểm của AB (giả thiết)

Và AI // CK hay KF // AE nên BF = EF (tính chất đường trung bình tam giác) (1)

Trong ΔDCF, ta có:

I là trung điểm của DC (giả thiết)

Và AI // CK hay IE // CF nên DE = EF (tính chất đường trung bình tam giác) (2)

Từ (1) và (2) suy ra:

DE = EF = FB (điều phải chứng minh).

Bài 79 trang 89 SBT Toán 8 Tập 1: Tính các góc của hình bình hành ABCD biết:

a) $\widehat{A}$ = 110^o

b) $\widehat{A}-\widehat{B}$ = 20^o

Lời giải:

a) Tứ giác ABCD là hình bình hành.

⇒ $\widehat{C}=\widehat{A}$ = 110^o (tính chất hình bình hành)

Lại có: $\widehat{A}+\widehat{B}$ = 180^o (2 góc trong cùng phía bù nhau)

⇒ $\widehat{B}$ = 180^o – 110^o = 70^o

$\widehat{D}=\widehat{B}$ = 70^o (tính chất hình bình hành)

b) Vì tứ giác ABCD là hình bình hành.

⇒ $\widehat{A}+\widehat{B}$ = 180^o (2 góc trong cùng phía bù nhau)

 Mà $\widehat{A}-\widehat{B}$ = 20^o (giả thiết)

Ta có:

$\widehat{A}+\widehat{B}+\widehat{A}-\widehat{B}=180°+20°$

Suy ra: 2 $\widehat{A}$ = 200^o 

⇒ $\widehat{A}$= 100^o

Do đó, $\widehat{C}=\widehat{A}$ =  100^o (tính chất hình bình hành)

$\widehat{B}=\widehat{A}$– 20^o = 100^o – 20^o = 80^o

$\widehat{D}=\widehat{B}$ = 80^o (tính chất hình bình hành)

Bài 80 trang 89 SBT Toán 8 Tập 1: Trong các tứ giác ở hình dưới đây, hình nào là hình bình hành.

Lời giải:

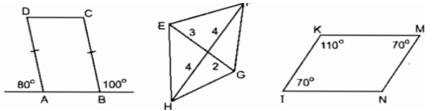
* Tứ giác ABCD là hình bình hành vì AB // CD và AB = CD.

* Tứ giác IKMN có: 

$\widehat{I}+\widehat{K}+\widehat{N}+\widehat{M}$  = 360^o

Suy ra:

 $\widehat{N}$ = 360^o - ( $\widehat{I}+\widehat{K}+\widehat{M}$) = 110^o

Ta có $\widehat{I}=\widehat{M}$ = 70^o và $\widehat{K}=\widehat{N}$ = 110^o

Suy ra IKMN là hình bình hành (tứ giác có các góc đối bằng nhau).

* Tứ giác EFGH không là hình bình hành vì có hai đường chéo không cắt nhau tại trung điểm mỗi đường.

Bài 81 trang 90 SBT Toán 8 Tập 1: Chu vi hình bình hành ABCD bằng l0cm, chu vi tam giác ABD bằng 9cm. Tính độ dài BD.

Lời giải:

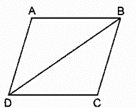
Chu vì hình bình hành ABCD bằng 10cm nên

(AB + AD).2 = 10(cm)

⇒ AB + AD = 10 : 2 = 5(cm)

Chu vi của ΔABD bằng:

AB + AD + BD = 9(cm)

⇒ BD = 9 - (AB + AD)

= 9 - 5 = 4(cm)

Bài 82 trang 90 SBT Toán 8 Tập 1: Trên hình 10, cho ABCD là hình bình hành. Chứng minh rằng AE //CF.

Lời giải:

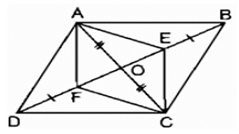
Gọi O là giao điểm của AC và BD, ta có:

OB = OE + EB và OD = OF + FD (1)

Lại có: EB = FD (giả thiết) (2)

OB = OD (tính chất hình bình hành). (3)

Từ (1), (2),(3) suy ra: OE = OF.

Lại có: O là trung điểm của AC nên OA = OC

Xét tứ giác AECF có:

O là trung điểm của AC

O là trung điểm của EF

Suy ra tứ giác AECF là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ AE // CF (tính chất hình bình hành).

Bài 83 trang 90 SBT Toán 8 Tập 1: Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng:

a) EMNF là hình bình hành;

b) Các đường thẳng AC, EF, MN đồng quy.

Lời giải:

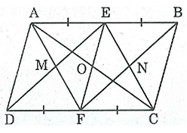
a)

+) Ta có:

AE = $\frac{1}{2}$AB; CF = $\frac{1}{2}$CD (vì E và F lần lượt là trung điểm của AB, CD).

Và AB = CD (tính chất hình bình hành)

Do đó, AE = CF.

+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF

Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành

⇒ AF //CE hay EN // FM (1).

Xét tứ giác BFDE ta có:

AB // CD (Vì ABCD là hình bình hành) hay BE // DF

Vì E và F lần lượt là trung điểm của AB, CD nên 

$BE\text{\hspace{0.17em}\hspace{0.17em}}=\frac{1}{2}\text{}AB;D\text{}F=\frac{1}{2}\text{}CD$

Lại có: AB = CD (tính chất hình bình hành)

Suy ra: BE = DF.

Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)

Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành).

b) Gọi O là giao điểm của AC và EF.

Tứ giác AECF là hình bình hành ⇒ OE = OF (tính chất hình bình hành).

Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Suy ra: MN đi qua trung điểm O của EF.

Vậy AC, EF, MN đồng quy tại O.

Bài 84 trang 90 SBT Toán 8 Tập 1: Trên hình 11, cho ABCD là hình bình hành. Chứng minh rằng:

a) EGFH là hình bình hành.

b) Các đường thẳng AC, BD, EF, GH đồng quy.

Hình 11

Lời giải:

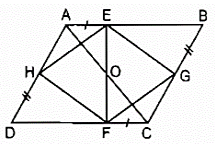
a)

+) Ta có: AH + HD = AD

Và CG + GB = CB

Mà AD = CB (vì ABCD là hình bình hành).

 Và DH = GB (giả thiết)

Suy ra: AH = CG.

Xét ΔAEH và ΔCFG:

AE = CF (giả thiết)

$\widehat{A}=\widehat{C}$ (tính chất hình bình hành)

AH = CG ( chứng minh trên).

Do đó: ΔAEH = ΔCFG (c.g.c)

⇒ EH = FG.

Xét ΔBEG và ΔDFH, ta có:

BG = DH (giả thiết)

$\widehat{B}=\widehat{D}$ (tính chất hình bình hành)

BE = DF (vì AB = CD và AE = CF nên AB – AE = CD – CF hay BE = DF )

Do đó: ΔBEG = ΔDFH (c.g.c)

⇒ EG = FH

Xét tứ giác EGFH có:

EG = HF (chứng minh trên)

EH = FG (chứng minh trên)

Suy ra: Tứ giác EGFH là hình bình hành (vì có các cặp cạnh đối bằng nhau).

b) Gọi O là giao điểm của AC và EF.

Xét tứ giác AECF, ta có: AB // CD ( Vì ABCD là hình bình hành) hay AE // CF

Lại có: AE = CF (giả thiết)

Do đó: Tứ giác AECF là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).

⇒ O là trung điểm của AC và EF.

Tứ giác ABCD là hình bình hành có O là trung điểm AC nên O cũng là trung điểm của BD.

Tứ giác EGFH là hình bình hành có O là trung điểm EF nên O cũng là trung điểm của GH.

Vậy AC, BD, EF, GH đồng quy tại O.

Bài 85 trang 90 SBT Toán 8 Tập 1: Cho hình hình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng minh rằng AA' = BB' + DD'.

Lời giải:

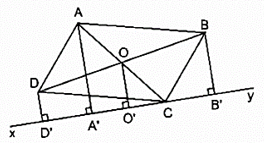
Gọi O là giao điểm của hai đường chéo AC và BD.

Kẻ OO' ⊥ xy

Ta có: BB' ⊥ xy (giả thiết)

DD' ⊥ xy (giả thiết)

Suy ra: BB // OO' // DD'

Tứ giác BB'D'D là hình thang .

OB = OD (tính chất hình bình hành)

Nên O'B' = O'D'

Do đó OO' là đường trung bình của hình thang BB'D'D

⇒ $OO\text{'}=\frac{BB\text{'}+D\text{}D\text{'}}{2}$ (tính chất đường trung hình hình thang) (1)

Ta có: AA' ⊥ xy (giả thiết)

Và OO' ⊥ xy (theo cách vẽ)

Suy ra: AA' // OO'.

Trong ΔACA' tacó:

OA = OC (tính chất hình bình hành)

OO' // AA' nên OO' là đường trung bình của ΔACA'

⇒OO' = $\frac{1}{2}$AA' (tính chất đường trung bình của tam giác)

⇒AA' = 2OO' (2).

Từ (1) và (2) suy ra:

AA' = BB' + DD'  (điều phải chứng minh).

Bài 86 trang 90 SBT Toán 8 Tập 1: Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA’; BB’; CC’; DD’ là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy.

Tìm mối liên hệ độ dài giữa AA', BB', CC', DD'.

Lời giải:

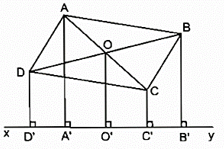
Gọi O là giao điểm của AC và BD.

⇒ OA = OC, OB = OD (tính chất hình bình hành).

Kẻ OO' ⊥ xy

Ta có: AA' ⊥ xy (giả thiết)

Và CC' ⊥ xy (giả thiết)

Suy ra: AA' // OO' // CC'.

Tứ giác ACC'A' là hình thang có:

OA = OC (chứng minh trên)

Và OO' // AA' nên OO' là đường trung bình của hình thang ACC'A'.

⇒ OO' = $\frac{AA\text{'}+CC\text{'}}{2}$ (tính chất đường trung bình của hình thang) (1)

Ta có: BB' ⊥ xy

DD' ⊥ xy (gt)

OO' ⊥ xy (gt)

Suy ra: BB'// OO' // DD'

Tứ giác BDD'B' là hình thang có:

OB = OD (chứng minh trên)

OO' // BB' nên OO' là đường trung bình của hình thang BDD'B'.

⇒ $OO\text{'}=\frac{BB\text{'}+D\text{}D\text{'}\text{\hspace{0.17em}\hspace{0.17em}}}{2}$ (tính chất đường trung bình của hình thang) (2)

Từ (1) và (2) suy ra:

AA' + CC' = BB + DD'

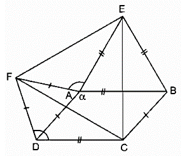
Bài 87 trang 90 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có $\hat{A}$ = α > 90^o. Ở phía ngoài hình bình hành vẽ các tam giác đều ADF, ABE

a) Tính $\widehat{E\text{}A\text{}F}$;

b) Chứng minh rằng tam giác CEF là tam giác đều.

Lời giải:

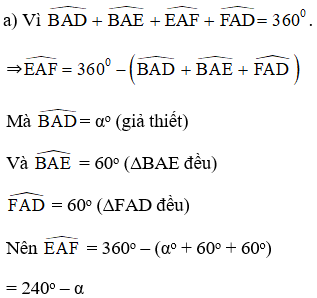
Bài 88 trang 90 SBT Toán 8 Tập 1: Cho tam giác ABC. Ở phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng:

a) IA = BC;

b) IA ⊥ BC.

Lời giải:

Bài 89 trang 91 SBT Toán 8 Tập 1: Dựng hình bình hành ABCD biết:

a) AB = 2cm, AD = 3cm, $\hat{A}$ = 110^o;

b) AC = 4cm, BD = 5cm, $\widehat{BOC}$ = 50^o.

Lời giải:

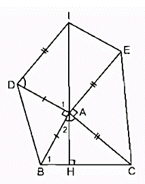
a) Cách dựng (hình a)

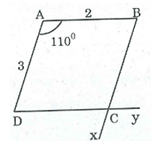
- Dựng ΔABD có AB = 2cm, $\hat{A}$ = 110^o, AD = 3cm

- Dựng tia Bx //AD

- Dựng tia Dy // AB và Dy cắt Bx tại C

Ta có hình bình hành ABCD cần dựng

Chứng minh

AB //CD, AD // BC nên tứ giác ABCD là hình bình hành.

Ta lại có: AB = 2cm, $\hat{A}$ = 110^o, AD = 3cm.

Bài toán có một nghiệm hình.

b) Cách dựng (hình b)

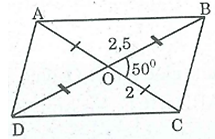
- Dựng ΔOBC có OC = 2cm, OB = 2,5 cm, $\widehat{BOC}$ = 50^o

- Trên tia đối tia OC lấy điểm A sao cho OA = OC = 2cm.

- Trên tia đối tia OB lấy điểm D sao cho OD = OB =2,5cm.

Nối AB, BC, CD, AD ta có hình bình hành ABCD cần dựng

Chứng minh

Tứ giác ABCD có OA = OC, OB = OD nên nó là hình bình hành vì có 2 đường chéo cắt nhau tại trung điểm mỗi đường.

Có AC = 4cm , BD = 5cm, $\widehat{BOC}$ = 50^o

Bài toán có một nghiệm hình.

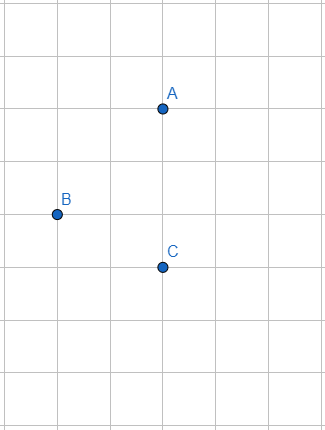
Bài 90 trang 91 SBT Toán 8 Tập 1: Cho ba điểm A, B, C trên giấy kẻ ô vuông ở hình bên. Hãy vẽ điểm thứ tư M sao cho A, B,C, M là 4 đỉnh của một hình bình hành.

Lời giải:

- Nếu hình bình hành nhận AC làm đường chéo.

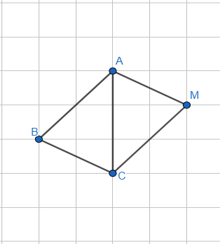
Vì AB là đường chéo hình vuông có 2 ô vuông nên CM là đường chéo hình vuông cạnh 2 ô vuông và A, M nằm trên một nửa mặt phẳng bờ BC ta có hình bình hành ABCM

- Nếu hình bình hành nhận BC làm đường chéo.

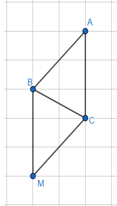
Điểm A cách điểm C ba ô vuông, điểm B cách điểm M là ba ô vuông và trên một nửa mặt phẳng bờ AB ta có hình bình hành ABMC

- Nếu hình bình hành nhận AB làm đường chéo

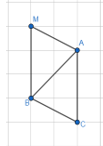
Điểm M cách điểm B ba ô vuông, M và A nằm trên cùng một nửa mặt phẳng bờ BC ta có hình bình hành ACBM.

Bài 91 trang 91 SBT Toán 8 Tập 1: Cho tam giác ABC. Dựng đường thẳng song song với BC, cắt cạnh AB ở E, cắt cạnh AC ở F sao cho BE = AF.

Lời giải:

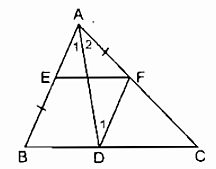
Cách dựng:

- Dựng đường phân giác AD của góc $\widehat{BAC}$.

- Qua D dựng đường thẳng song song AB cắt AC tại F.

- Qua F dựng đường thẳng song song với BC cắt AB tại E.

Ta có đường thẳng đi qua hai điểm E, F là đường thẳng cần dựng.

Chứng minh:

Ta có: DF // AB

⇒ $\widehat{A_1}=\widehat{D_1}$ (so le trong)

Lại có: $\widehat{A_1}=\widehat{A_2}$ (vì AD là tia phân giác của góc BAC).

Suy ra: $\widehat{D_1}=\widehat{A_2}$

⇒ ΔAFD cân tại F ⇒ AF = DF (l).

Ta có: DF // AB hay DF // BE

 Và EF // BC hay EF // BD.

Suy ra: tứ giác BDFE là hình bình hành

⇒ BE = DF (2)

Từ (1) và (2) suy ra: AF = BE.

Bài tập bổ sung

Bài 7.1 trang 91 SBT Toán 8 Tập 1: Tứ giác ABCD là hình bình hành nếu: A. AB = CD...

Bài 7.2 trang 91 SBT Toán 8 Tập 1: Cho hình bình hành ABCD , các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB...

Bài 7.3 trang 91 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF...

Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

Bài 8: Đối xứng tâm

Bài 9: Hình chữ nhật

Bài 10: Đường thẳng song song với một đường thẳng cho trước

Bài 11: Hình thoi

Bài 12: Hình vuông

Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

Trắc nghiệm Hình bình hành có đáp án