Nội dung bài viết

    Xem thêm

    Hình thang vuông ABCD (AB // CD) có đường chéo BD vuông góc với cạnh BC tại B

    Với giải Bài 7.2 trang 94 SBT Toán 8 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

    1 2,700 14/05/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ ba (g.g)

    Bài 7.2 trang 94 sách bài tập Toán 8 Tập 2: Hình thang vuông ABCD (AB // CD) có đường chéo BD vuông góc với cạnh BC tại B và có độ dài BD = m = 7,25cm. Hãy tính độ dài các cạnh của hình thang, biết rằng BC = n = 10,75cm.

    (Tính chính xác đến hai chữ số thập phân).

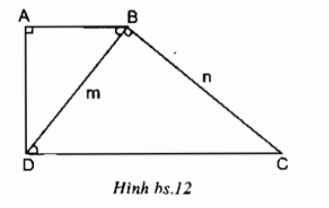
    Tài liệu VietJack

    Lời giải:

    Theo giả thiết ABCD là hình thang vuông và AB // CD, BD ⊥ BC nên ta có:

    DAB^=CBD^=90°

    ABD^=BDC^ (so le trong)

    Do đó: ΔABD đồng dạng ΔBDC

    ⇒ABBD  =  ADBC = BDDC   (1)

    Xét tam giác vuông DBC, theo định lí Pi-ta-go , ta có:

    DC=  BD2+​ BC2  =  m2+​n2

    Từ dãy tỉ lệ thức (1), tính được:

    AB= BD2DC  =  m2m2+n2;  AD=  BC.BDDC  =  mnm2+n2

    Với m = 7,25cm, n = 10,75 cm, ta tính được:

    DC ≈ 12,97cm; AB ≈ 4,05cm; AD ≈ 6,01cm.

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 39 trang 93 SBT Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD...

    Bài 40 trang 93 SBT Toán 8 Tập 2: Tam giác vuông ABC có A^=90°  và đường cao AH. Từ H hạ HK vuông góc với AC...

    Bài 41 trang 94 SBT Toán 8 Tập 2: Hình thang ABCD (AB // CD) có AB = 2,5cm, AD = 3,5cm, BD = 5cm và DAB^=DBC^...

    Bài 42 trang 94 SBT Toán 8 Tập 2: Cho tam giác vuông ABC có A^=90°. Dựng AD vuông góc với BC (D thuộc BC). Đường phân giác BE cắt AD tại F...

    Bài 43 trang 94 SBT Toán 8 Tập 2: Chứng minh rằng nếu hai tam giác ABC và A'B'C' đồng dạng với nhau thì...

    Bài 7.1 trang 94 SBT Toán 8 Tập 2: Hình bs.5 cho biết tam giác ABC có hai đường cao AD và BE cắt nhau tại H...

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,700 14/05/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: