Cho hình bình hành ABCD có AB = 2AD. Gọi E và F theo thứ tự là
Với giải bài 162 trang 100 sbt Toán lớp 8 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài: Ôn tập chương 1 - Phần Hình học
Bài 162 trang 100 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có AB = 2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD.
a) Các tứ giác AEFD, AECF là hình gì? Vì sao?
b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
c) Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông.
Lời giải:
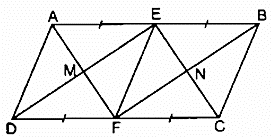
a) * Xét tứ giác AEFD, ta có:
AB // CD (vì ABCD là hình bình hành) hay AE // FD
AE = AB (vì E là trung điểm AB)
FD = CD (vì F là trung điểm của CD)
Suy ra: AE = FD.
Do đó, tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
Lại có: AD = AE = AB .
Vậy tứ giác AEFD là hình thoi.
* Xét tứ giác AECF, ta có:
AE // CF (do ABCD là hình bình hành)
AE = AB (giả thiết)
CF = CD (giả thiết)
Suy ra: AE = CF.
Tứ giác AECF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
b) Tứ giác AEFD là hình thoi
⇒ AF ⊥ ED ⇒ = 90o
AF // CE (vì tứ giác AECF là hình bình hành)
Mà AF ⊥ ED
Nên CE ⊥ ED ⇒ = 90o
Xét tứ giác EBFD, ta có:
EB = FD (vì cùng bằng AE)
EB // FD (vì AB // CD)
Tứ giác EBFD là hình bình hành (vì có một cặp cạnh đổi song song và bằng nhau) ⇒ DE // BF
Mà DE ⊥ AF
Nên BF ⊥ AF ⇒ = 90°
Xét tứ giác MENF có:
= 90°
= 90o
= 90o
Vậy tứ giác EMFN là hình chữ nhật.
c) Ta có: Hình chữ nhật EMFN là hình vuông ⇒ ME = MF
ME = DE (tính chất hình thoi)
MF = AF (tính chất hình thoi)
Suy ra: DE = AF.
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ = 90o ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ = 90o
Hình thoi AEFD có = 90o nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.
Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:
Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
