Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC
Với giải bài 158 trang 100 sbt Toán lớp 8 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài: Ôn tập chương 1 - Phần Hình học
Bài 158 trang 100 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
a) Tứ giác AEDF là hình gì? Vì sao?
b) Các tứ giác ADBM, ADCN là hình gì? Vì sao?
c) Chứng minh rằng M đối xứng với N qua A.
d) Tam giác ABC có điều kiện gì thì tứ giác AEDF là hình vuông.
Lời giải:
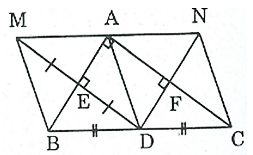
a) Điểm M và điểm D đối xứng qua trục AB
Suy ra AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM ⇒ = 90o
Điểm D và điểm N đối xứng qua trục AC
⇒ AC là đường trung trực của đoạn thẳng DN
⇒ AC ⊥ DN ⇒ = 90°
Xét tứ giác AEDF có
= 90o (giả thiết)
= 90°
= 90o
Vậy tứ giác AEDF là hình chữ nhật (vì có 3 góc vuông).
b) Tứ giác AEDF là hình chữ nhật
⇒ DE // AC; DF // AB
Trong ∆ABC, ta có:
DB = DC (giả thiết)
Mà DE // AC
Suy ra: AE = EB (tính chất đường trung bình của tam giác)
Lại có: DF // AB và DB = DC
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM, ta có:
AE = EB (chứng minh trên)
ED = EM (vì AB là trung trực DM)
Suy ra tứ giác ADBM là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mặt khác: AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi (vì có hai đường chéo vuông góc)
Xét tứ giác ADCN, ta có:
AF = FC (chứng minh trên)
DF = FN (vì AC là đường trung trực DN)
Suy ra tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Lại có: AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
c) Tứ giác ADBM là hình thoi
⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi
⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng.
Và AM = AN nên A là trung điểm của MN.
Vậy điểm M và điểm N đối xứng qua điểm A.
d) Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = AB; AF = AC
Nên AE = AF ⇒ AB = AC.
Vậy nếu ∆ABC vuông cân tại A thì tứ giác AEDF là hình vuông.
Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:
Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
