Nội dung bài viết

    Xem thêm

    Cho tam giác đều ABC. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CA, AB

    Với giải Bài 1.2 trang 156 SBT Toán 8 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

    1 2,011 07/05/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 1: Đa giác. Đa giác đều

    Bài 1.2 trang 156 SBT Toán 8 Tập 1: a) Cho tam giác đều ABC. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.

    b) Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều).

    c) Cho ngũ giác đều ABCDE. Gọi M, N, P, Q, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.

    Lời giải:

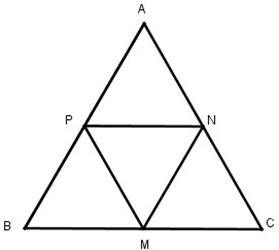
    Tài liệu VietJack

    a) Ta có: M là trung điểm của BC và N là trung điểm của AC

    Nên MN là đường trung bình của Δ ABC

    ⇒ MN = 12AB

    Ta có: P là trung điểm của AB; M là trung điểm BC nên MP là đường trung bình của Δ ABC

    ⇒ MP = 12AC

    Tương tự, NP là đường trung bình của Δ ABC

    ⇒ NP = 12BC.

    Mà AB = BC = AC (vì tam giác ABC đều)

    Do đó MN = MP = NP. Vậy Δ MNP đều.

    b) Do ABCD là hình vuông có M, N, P, Q lần lượt là trung điểm của BC, CD, DA, AB nên: AQ = QB = BM = MC = CN = ND = DP = PA

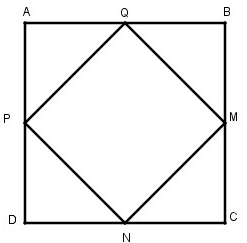
    Tài liệu VietJack

    Xét Δ APQ và Δ BQM:

    AQ = BM

    A^  =  B^ = 90o

    AP = BQ

    Do đó: Δ APQ = Δ BQM (c.g.c)

    ⇒ PQ = QM (1)

    Xét Δ BQM và Δ CMN:

    BM = CN

    B^  =  C^= 90o

    BQ = CM

    Do đó: Δ BQM = Δ CMN (c.g.c)

    ⇒ QM = MN (2)

    Xét Δ CMN và Δ DNP:

    CN = DP

    C^  =  D^= 90o

    CM = DN

    Do đó: Δ CMN = Δ DNP (c.g.c)

    ⇒ MN = NP (3)

    Từ (1), (2) và (3) suy ra:

    MN = NP = PQ = QM.

    Suy ra:  tứ giác MNPQ là hình thoi

    Vì AP = AQ nên Δ APQ vuông cân tại A

    BQ = BM nên Δ BMQ vuông cân tại B

    Do đó: AQP^  =  BQM^ = 45o

    Lại có:

    AQP^  +​ PQM^  +​ BQM^ = 180o (kề bù)

    ⇒PQM^ =  1800− AQP^  +​ BQM^ 

    = 180o - (45o + 45o) = 90o

    Vậy tứ giác MNPQ là hình vuông.

    c)

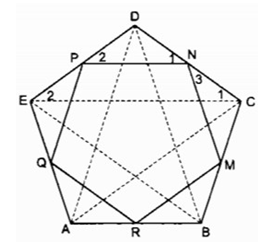
    Tài liệu VietJack

    Xét Δ ABC và Δ BCD:

    AB = BC (vì ABCDE là ngũ giác đều)

    B^  =  C^ (vì ABCDE là ngũ giác đều)

    BC = CD ( vì ABCDE là ngũ giác đều).

    Do đó: Δ ABC = Δ BCD (c.g.c)

    ⇒ AC = BD (1)

    Tương tự, xét Δ BCD và Δ CDE:

    BC = CD

    C^  =  D^

    CD = DE

    Do đó: Δ BCD = Δ CDE (c.g.c)

    ⇒ BD = CE (2)

    Xét Δ CDE và Δ DEA:

    CD = DE

    D^  =  E^

    DE = EA

    Do đó: Δ CDE = Δ DEA (c.g.c)

    ⇒ CE = DA (3)

    Xét Δ DEA và Δ EAB:

    DE = EA

    E^  =  A^

    EA = AB

    Do đó: Δ DEA = Δ EAB (c.g.c)

    ⇒ DA = EB (4)

    Từ (1), (2), (3), (4) suy ra:

    AC = BD = CE = DA = EB

    Trong Δ ABC ta có RM là đường trung bình

    ⇒ RM = 12AC (tính chất đường trung bình của tam giác).

    Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình

    ⇒ MN = 12BD (tính chất đường trung bình của tam giác)

    Trong Δ CDE ta có NP là đường trung bình

    ⇒ NP = 12CE (tính chất đường trung bình của tam giác)

    Trong Δ DEA ta có PQ là đường trung bình

    ⇒ PQ = 12DA (tính chất đường trung bình của tam giác)

    Trong Δ EAB ta có QR là đường trung bình

    ⇒ QR = 12EB (tính chất đường trung bình của tam giác)

    Suy ra:

    MN = NP = PQ = QR = RM

    Ta có:

    A^  =  B^  = C^  =  D^  =  E^ 

    = (​5−2).18005 = 108o

    Vì Δ DPN cân tại D

     ⇒DPN^  = DNP^  =  1800− D^2 = 1800−10802  =360

    Vì Δ CNM cân tại C

    ⇒CNM^  = CMN^  =  1800− D^2 = 1800−10802  =360

    Mà DNP^  +​ PNM^  +​  CNM^  =1800

    ⇒ PNM^=  1800−(​ DNP^  +​  CNM^ )

    =180o - (36o – 36o) = 108o

    Vì Δ BMR cân tại B

     ⇒BMR^ = BRM^  = 1800−  B^2  = 1800−10802 =360

    Mà:

    CMN^  ​​+​  NMR^  +​  BMR^  =1800⇒NMR^  =1800−  (CMN^  +​  BMR^)

    = 180o - (36o – 36o) = 108o

    Vì Δ ARQ cân tại A

    ⇒A​RQ^ = AQR^  = 1800−A^2  =  1800−10802  =360

    Mà BRM^ ​+ MRQ^ +​ AR​Q^  =1800

    ⇒ MRQ^ ​=3600−  BR​M^ +​ AR​Q^  

    =180o - (36o – 36o) = 108o

    Vì Δ QEP cân tại E

    ⇒EQP^ = EPQ^  = 1800−E^2  =  1800−10802  =360

    Mà AQR^  +​ R​QP^  +​ EQP^  =1800

    ⇒ RQP^ =1800− ​ A​QR^  +​ EQP^  

    = 180o - (36o – 36o) = 108o

    Mà EPQ^  +  QPN^  + DPN^ =1800

    ⇒ QPN^=  1800− ( EPQ^  + DPN^ )

    = 180o - (36o – 36o) = 108

    Suy ra:

     PNM^ =  NMR^  = MRQ^  = RQP^  = QPN^

    Vậy MNPQR là ngũ giác đều.

    Xem thêm lời giải sách bài tập Toán lớp 8 hay, chi tiết khác:

    Bài 1 trang 155 SBT Toán 8 Tập 1: Trong các hình dưới đây hình nào là đa giác lồi? Vì sao?...

    Bài 2 trang 155 SBT Toán 8 Tập 1: Hình vẽ bên. Hãy vẽ một đa giác lồi mà các đỉnh là một trong các điểm đã cho trong hình...

    Bài 3 trang 155 SBT Toán 8 Tập 1: Em hãy kể tên một số đa giác đều mà em biết...

    Bài 4 trang 156 SBT Toán 8 Tập 1: Chứng minh rằng số đo của một hình n-giác đều là...

    Bài 5 trang 156 SBT Toán 8 Tập 1: Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều...

    Bài 6 trang 156 SBT Toán 8 Tập 1: a) Vẽ hình và tính số đường chéo của ngũ giác, lục giác...

    Bài 7 trang 156 SBT Toán 8 Tập 1: Tìm số đường chéo của hình 8 cạnh, 10 cạnh, 12 cạnh...

    Bài 8 trang 156 SBT Toán 8 Tập 1: Chứng minh rằng tổng các góc ngoài của một đa giác (lồi) có số đo bằng 360o...

    Bài 9 trang 156 SBT Toán 8 Tập 1: Đa giác nào có tổng số đo các góc trong bằng tổng số đo các góc ngoài?...

    Bài 10 trang 156 SBT Toán 8 Tập 1: Một đa giác (lồi) có nhiều nhất là bao nhiêu góc nhọn?...

    Bài 11 trang 156 SBT Toán 8 Tập 1: Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác đó bằng 468°...

    Bài 1.1 trang 156 SBT Toán 8 Tập 1: Mỗi câu sau đây đúng hay sai ?...

    Bài 1.3 trang 157 SBT Toán 8 Tập 1: Cho hình vuông ABCD có AB = 3cm Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm...

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,011 07/05/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: