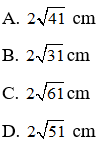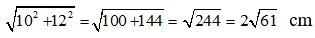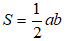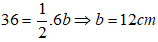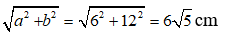TOP 40 câu trắc nghiệm Diện tích hình chữ nhật (có đáp án 2023) - Toán 8
Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 2: Diện tích hình chữ nhật có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 2.
Trắc nghiệm Toán 8 Bài 2: Diện tích hình chữ nhật
Bài giảng Trắc nghiệm Toán 8 Bài 2: Diện tích hình chữ nhật
Bài 1: Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật
A. Không thay đổi
B. Tăng 2 lần
C. Giảm 2 lần
D. Tăng lần
Đáp án: B
Giải thích:
Theo công thức tính diện tích hình chữ nhật S = a.b thì diện tích hình chữ nhât tỉ lệ thuận với chiều dài và chiều rộng của nó
Nếu a’ = 4a; b’ = b thì
S’ = a’.b’ = 4a. b
= a.b = S = 2S
Do đó diện tích tăng 2 lần so với diện tích đã cho.
Bài 2: Cho tam giác ABC vuông tại A, vẽ hình chữ nhât ABDC. Biết diện tích của tam giác vuông là 140 cm2. Diện tích hình chữ nhật ABDC là:
A. 70 cm2
B. 280 cm2
C. 300 cm2
D. 80 cm2
Đáp án: B
Giải thích:
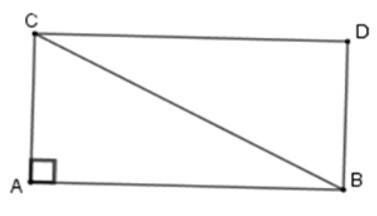
Vì ABDC là hình chữ nhật nên
SABDC = AC. AB
mà SABC =
nên SABCD = 2SABC
= 2.140 = 280 cm2.
Bài 3: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA.
Biết diện tích của tứ giác ABCD là 18 m2 thì diện tích của tứ giác EFGH là:
A. 9 m2
B. 5 m2
C. 6 m2
D. 7, 5 m2
Đáp án: A
Giải thích:
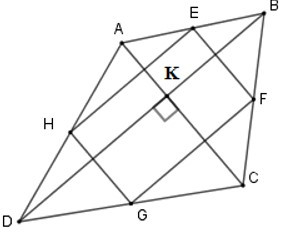
+ Vì E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA nên EF, FG, GH, HE lần lượt là đường trung bình của các tam giác ABC, BCD, ADC, ADB
nên EF//HG (vì cùng song song với AC); HE//FG (vì cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành, mà AC ⊥ BD (gt)
=> EFGH là hình chữ nhật.
Do đó SEFGH = HE. EF,
mà EF = AC; HE = BD (tính chất đường trung bình)
Nên SEFGH = AC. BD
= AC. BD.
+ Gọi K là giao của AC và BD.
Khi đó SABCD = SABC + SACD
= BK. AC + DK. AC
= AC (BK + DK)
= AC. BD
Mà SABCD = 18 m2
=> AC. BD = 18
=> AC. BD = 36 m2
suy ra SEFGH = AC. BD
= .36 = 9 m2
Bài 4: Hình chữ nhật có chiều dài giảm đi 5 lần, chiều rộng tăng lên 5 lần, khi đó diện tích hình chữ nhật
A. Không thay đổi.
B. Tăng 5 lần.
C. Giảm 5 lần.
D. Giảm 3 lần.
Đáp án: A
Giải thích:
Gọi a; b lần lượt là chiều dài và chiều rộng của hình chữ nhật ban đầu.
Diện tích hình chữ nhật ban đầu là S = a.b
Nếu giảm chiều dài đi 5 lần thì chiều dài mới
là a’ =a
Nếu tăng chiều rộng lên 5 lần thì chiều rộng mới là b’ = 5b
Lúc này, diện tích hình chữ nhật mới là
S’ = a’.b’ = a. 5b = ab = S
Do đó diện tích hình chữ nhật không thay đổi.
Bài 5: Cho tam giác ABC vuông tại A, vẽ hình chữ nhât ABDC. Biết diện tích của tam giác vuông là 55 cm2. Diện tích hình chữ nhật ABDC là:
A. 110 cm2
B. 55 cm2
C. 220 cm2
D. 100 cm2
Đáp án: A
Giải thích:
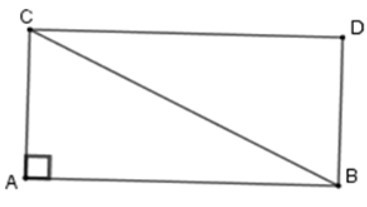
Vì ABDC là hình chữ nhật nên
SABDC = AC. AB
mà SABC =
nên SABCD = 2SABC
= 2.55 = 110 cm2.
Bài 6: Hình chữ nhật có chiều dài giảm 6 lần, chiều rộng tăng 3 lần, khi đó diện tích hình chữ nhật
A. Không thay đổi
B. Tăng 2 lần
C. Giảm 2 lần
D. Tăng lần
Đáp án: C
Giải thích:
Theo công thức tính diện tích hình chữ nhật S = a.b thì diện tích hình chữ nhât tỉ lệ thuận với chiều dài và chiều rộng của nó
Nếu a’ = ; b’ = 3b
thì S’ = a’.b’ = a. 3b
= ab = S = S
Do đó diện tích mới giảm 2 lần so với diện tích đã cho.
Bài 7: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA.
Biết diện tích của tứ giác ABCD là 40 m2 thì diện tích của tứ giác EFGH là:
A. 30 m2
B. 25 m2
C. 40 m2
D. 20 m2
Đáp án: D
Giải thích:
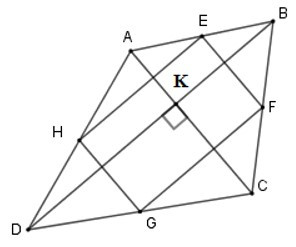
+ Vì E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA nên EF, FG, GH, HE lần lượt là đường trung bình của các tam giác ABC, BCD, ADC, ADB
nên EF//HG (vì cùng song song với AC); HE//FG (vì cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành, mà AC ⊥ BD (gt)
=> EFGH là hình chữ nhật.
Do đó SEFGH = HE. EF,
mà EF = AC; HE = BD (tính chất đường trung bình)
Nên SEFGH = AC. BD = AC. BD.
+ Gọi K là giao của AC và BD.
Khi đó SABCD = SABC + SACD
= BK. AC + DK. AC
= AC (BK + DK)
= AC. BD
Mà SABCD = 40 m2
=> AC. BD = 40
=> AC. BD = 80 m2
suy ra SEFGH = AC. BD
= .80 = 20 m2
Bài 8: Trong các hình chữ nhật có cùng chu vi 100 cm, hình có diện tích lớn nhất là bao nhiêu?
A. 2500 cm2
B. 625 cm2
C. 500 cm2
D. 1250 cm2
Đáp án: B
Giải thích:
Nửa chu vi của hình chữ nhật là: 100 : 2 = 50cm.
Gọi một kích thước của hình chữ nhật là x (cm; x > 0) thì kích thước còn lại là 50 – x (cm).
Diện tích hình chữ nhật bằng
x. (50 – x) = –x2 + 50x
= – (x2 – 50x + 625) +625
= 625 – (x – 25)2.
Ta có: (x – 25)2 ≥ 0; Ɐx
625 – (x – 25)2 ≤625; Ɐx
Dấu “=” xảy ra khi x = 25.
Vậy hình chữ nhật có diện tích lớn nhất là 625 cm2.
Bài 9: Một hình chữ nhât có diện tích là 120 cm2, chiều dài là 15 cm. Chu vi hình chữ nhật đó là:
A. 23 cm
B. 46 cm
C. 19 cm
D. 38 cm
Đáp án: B
Giải thích:
Gọi chiều rộng hình chữ nhật là a, ta có S = a.15
15a = 120 a = 8 cm
Chu vi hình chữ nhật là
S = (15+8). 2 = 46 cm.
Bài 10: Một hình chữ nhât có diện tích là 24 cm2, chiều dài là 8 cm. Chu vi hình chữ nhật đó là:
A. 11 cm
B. 20 cm
C. 22 cm
D. 16 cm
Đáp án: C
Giải thích:
Gọi chiều rộng hình chữ nhật là a, ta có
S = a.8 8a = 24
a = 3 cm
Chu vi hình chữ nhật là
S = (a+8). 2 = 22 cm.
Bài 11: Diện tích hình chữ nhật thay đổi như thế nào nếu chiều rộng tăng 4 lần, chiều dài giảm 2 lần ?
A. Diện tích không đổi.
B. Diện tích giảm 2 lần.
C. Diện tích tăng 2 lần.
D. Cả đáp án A, B, C đều sai.
Đáp án: C
Giải thích:
Công thức diện tích hình chữ nhật là Shcn = a.b
Trong đó : a là chiều dài, b là chiều rộng
Theo giả thiết: Sban đầu = a.b
Khi đó ta có: Ssau = 4b.1/2a = 2a.b = 2Sban đầu
Do đó, diện tích sau tăng lên 2 lần.
Bài 12: Cho hình chữ nhật có chiều dài là 4 cm, chiều rộng là 1,5 cm. Diện tích của hình chữ nhật đó là ?
A. 5( cm )
B. 6( cm2 )
C. 6( cm )
D. 5( cm2 )
Đáp án: B
Giải thích:
Công thức diện tích hình chữ nhật là Shcn = a.b
Trong đó : a là chiều dài, b là chiều rộng
Khi đó ta có: Shcn = 4. 1,5 = 6( cm2 ).
Bài 13: Cho hình vuông có độ dài cạnh hình vuông là 4 cm. Diện tích của hình vuông đó là?
A. 8( cm ).
B. 16( cm )
C. 8( cm2 )
D. 16( cm2 )
Đáp án: D
Giải thích:
Diện tích hình vuông bằng bình phương cạnh của nó: S = a2.
Khi đó ta có Shv = 4.4 = 16 ( cm2 ).
Bài 14: Cho tam giác vuông, có độ dài hai cạnh góc vuông lần lượt là 6cm, 4cm. Diện tích của tam giác vuông đó là ?
A. 24( cm2 )
B. 14( cm2 )
C. 12( cm2 )
D. 10( cm2 )
Đáp án: C
Giải thích:
Diện tích tam giác vuông bằng nửa tích hai cạnh: S = 1/2a.b.
Khi đó ta có S = 1/2. 6. 4 = 12( cm2 ).
Bài 15: Cho hình vuông có đường chéo là 6( dm ) thì diện tích là ?
A. 12( cm2 )
B. 18( cm2 )
C. 20( cm2 )
D. 24( cm2 )
Đáp án: B
Giải thích:
Diện tích hình vuông bằng bình phương cạnh của nó: S = a2.
Ngoài công thức này, diện tích hình vuông còn một công thức mở rông là:
Diện tích hình vuông bằng nửa tích của hai đường chéo
Khi đó ta có : S = 1/2. 6. 6 = 18( cm2 ).
Bài 16: Cho một tam giác vuông có độ dài hai cạnh góc vuông là 8cm và 9cm. Một hình vuông khác có diện tích bằng diện tích tam giác. Tính độ dài cạnh hình vuông.
A. 6cm
B. 7cm
C. 4cm
D. 8cm
Đáp án: A
Giải thích:
Diện tích tam giác vuông là: S = (1/2).8.9 = 36cm2
Gọi độ dài cạnh hình vuông là a (cm).
Diện tích hình vuông là: S = a2 (cm2)
Vì diện tích hình vuông bằng diện tích tam giác nên: a2 = 36 nên a = 6cm
Chọn đáp án A
Bài 17: Một hình chữ nhật có chiều rộng là 10cm và diện tích là 120cm2. Tính đường chéo của hình chữ nhật?
Đáp án: C
Giải thích:
Diện tích hình chữ nhật là: S = a.b trong đó a và b lần lượt là chiều dài và chiều rộng của hình chữ nhật
Suy ra: 120 = a.10 nên a = 12
Đường chéo của hình chữ nhật là:
Chọn đáp án C
Bài 18: Một tam giác vuông có diện tích 36cm2 và độ dài 1 cạnh góc vuông là 6cm. Tính cạnh huyền?
Đáp án: B
Giải thích:
Diện tích tam giác vuông là:
trong đó a,b là độ dài 2 cạnh góc vuông
Suy ra:
Cạnh huyền của tam giác vuông là:
Bài 19: Một hình chữ nhật có độ dài hai cạnh là 3cm và 12cm. Một hình vuông có diện tích bằng diện tích hình chữ nhật. Tính độ dài cạnh hình vuông?
A. 5cm
B. 6cm
C. 4cm
D. 7cm
Đáp án: B
Giải thích:
Diện tích hình chữ nhật là: 3.12 = 36 cm2
Diện tích hình vuông độ dài cạnh bằng a là: S = a2 (cm2)
Theo giả thiết ta có: a2 = 36 nên a = 6cm
Bài 20: Khi tăng độ dài cạnh lên 2 lần thì diện tích hình vuông tăng lên bao nhiêu lần?
A. 2
B. 4
C. 6
D. 8
Đáp án: B
Giải thích:
Gọi độ dài cạnh hình vuông ban đầu là a
Diện tích ban đầu của hình vuông là a2
Độ dài cạnh hình vuông khi tăng lên 2 lần là 2a
Diện tích của hình vuông mới là (2a)2 = 4a2
Suy ra: diện tích hình vuông tăng lên 4 lần
Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:
Trắc nghiệm Diện tích hình chữ nhật có đáp án
Trắc nghiệm Diện tích tam giác có đáp án
Trắc nghiệm Diện tích hình thang có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án