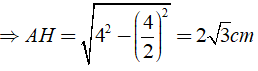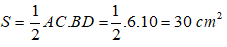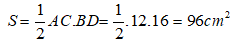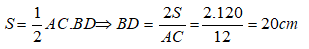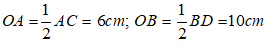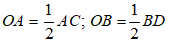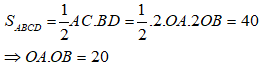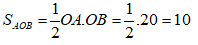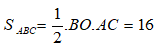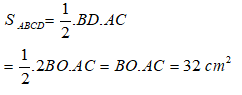TOP 40 câu Trắc nghiệm Diện tích hình thoi (có đáp án 2023) - Toán 8
Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 5: Diện tích hình thoi có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 5.
Trắc nghiệm Toán 8 Bài 5: Diện tích hình thoi
Bài giảng Trắc nghiệm Toán 8 Bài 5: Diện tích hình thoi
Bài 1: Hãy chọn câu đúng:
A. Diện tích của tứ giác có hai đường chéo vuông góc bằng tích hai đường chéo
B. Diện tích của tứ giác có hai đường chéo vuông góc bằng hiệu hai đường chéo
C. Diện tích của tứ giác có hai đường chéo vuông góc bằng tổng hai đường chéo
D. Diện tích của tứ giác có hai đường chéo vuông góc bằng nửa tích hai đường chéo
Đáp án: D
Giải thích:
Diện tích của tứ giác có hai đường chéo vuông góc bằng nửa tích hai đường chéo.
Bài 2: Hai đường chéo hình thoi có độ dài là 6 cm và 8 cm. Độ dài cạnh hình thoi là
A. 6 cm
B. 5 cm
C. 3 cm
D. 4 cm
Đáp án: B
Giải thích:
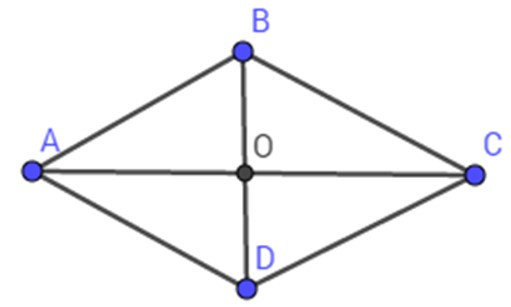
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O,
BD = 6 cm; AC = 8 cm.
Suy ra
BO = BD = .6 = 3 (cm);
AO = AC = .8 = 4 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB =
= = 5 (cm)
Bài 3: Hai đường chéo hình thoi có độ dài là 10 cm và 24 cm. Độ dài cạnh hình thoi là
A. 14 cm
B. 7 cm
C. 13 cm
D. 22 cm
Đáp án: C
Giải thích:
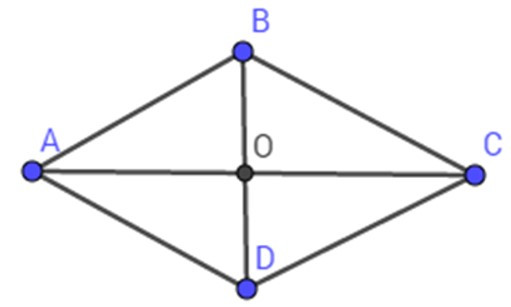
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O,
BD = 10 cm; AC = 24 cm.
Suy ra BO = BD = .12 = 6 (cm);
AO = AC = .24 = 12 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB =
= = 13 (cm)
Bài 4: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 10 cm, OA = 6cm. Diện tích hình thoi ABCD là:
A. 48 cm2
B. 96 cm2
C. 24 cm2
D. 40 cm2
Đáp án: B
Giải thích:
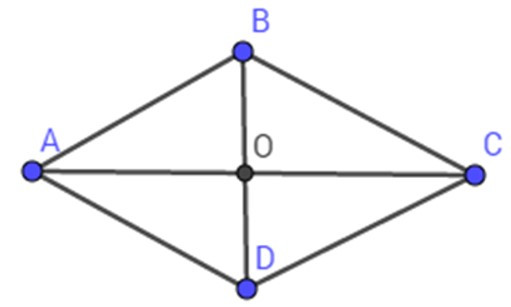
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO =
= = 8
SABCD = BD. AC
= .2OB. 2AO
= 2BO. AO = 2.8.6 = 96 (cm2)
Bài 5: Hình thoi có độ dài hai đường chéo là 15 cm và 20 cm. Tính độ dài đường cao của hình thoi.
A. 12 cm
B. 7, 5 cm
C. 15 cm
D. 24 cm
Đáp án: A
Giải thích:
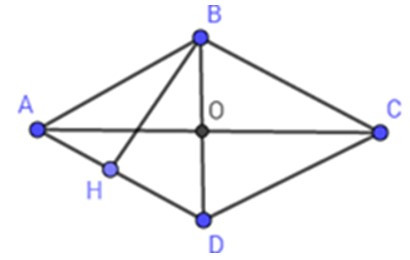
Giả sử hình thoi ABCD, đường chéo AC vuông góc với BD tại O, AC = 20 cm; BD = 15 cm. Gọi BH là đường cao hình thoi kẻ từ đỉnh B.
Ta có:
DO = BD = .15 = 7, 5 (cm);
AO = AC = .20 = 10 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOD vuông tại O ta có:
AD =
= = 12, 5 (cm)
SABCD = BD. AC
= 15.20 = 150 (cm2)
SABCD = BH. AD
=> BH =
= = 12 (cm)
Bài 6: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 10 cm, OA = 6cm. Diện tích hình thoi ABCD là:
A. 48 cm2
B. 96 cm2
C. 24 cm2
D. 40 cm2
Đáp án: B
Giải thích:
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO =
= = 8
SABCD = BD. AC
= 2OB. 2AO = 2BO. AO
= 2.8.6 = 96 (cm2)
Bài 7: Hình thoi có độ dài hai đường chéo là 6 cm và 8 cm. Tính độ dài đường cao của hình thoi.
A. 9,6 cm
B. 4,8 cm
C. 3,6 cm
D. 5,5 cm
Đáp án: B
Giải thích:
Giả sử hình thoi ABCD, đường chéo AC vuông góc với BD tại O,
AC = 8 cm; BD = 6 cm. Gọi BH là đường cao hình thoi kẻ từ đỉnh B.
Ta có: DO = BD = .6 = 3 (cm);
AO = AC = .8 = 4 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOD vuông tại O ta có:
AD =
= = 5 (cm)
SABCD = BD. AC
= 6.8 = 24 (cm2)
SABCD = BH. AD
=> BH = = = 4, 8 (cm)
Bài 8: Cho hình thoi có cạnh là 5 cm, một trong hai đường chéo có độ dài là 6 cm Diện tích của hình thoi là
A. 16 cm2
B. 12 cm2
C. 24 cm2
D. 32 cm2
Đáp án: C
Giải thích:
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD
tại O, AB = 5 cm; BD = 6 cm.
Suy ra BO = BD = .6 = 3 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AO = = = 4
SABCD = BD. AC = BD. 2AO
= BD.AO = 6.4 = 24 (cm2)
Bài 9: Cho hình thoi có cạnh là 10 cm, một trong hai đường chéo có độ dài là 16 cm Diện tích của hình thoi là
A. 192 cm2
B. 48 cm2
C. 96 cm2
D. 32 cm2
Đáp án: C
Giải thích:
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD
tại O, AB = 10 cm; AC = 16 cm.
Suy ra AO = AC = .16 = 8 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
OB = = = 6.
SABCD = BD. AC = 2OB. AC
= OB. AC = 6.16 = 96 (cm2)
Bài 10: Cho hình thoi MNPQ. Biết A, B, C, D lần lượt là các trung điểm của các cạnh NM, NP, PQ, QM.
Tính tỉ số diện tích của tứ giác ABCD và hình thoi MNPQ.
A.
B.
C. 2
D.
Đáp án: A
Giải thích:
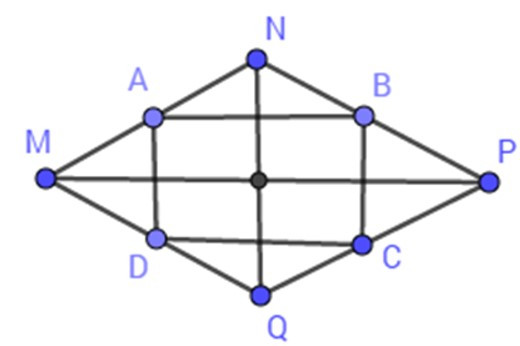
Xét tam giác MNP có: MA = AN; NB = BP (gt)
=> AB là đường trung bình của tam giác
MNP => AB = MP; AB // MP (1) (tính chất đường trung bình của tam giác).
Xét tam giác MQP có: MD = DQ; PC = CQ (gt)
=> CD là đường trung bình của tam giác
MQP => CD = MP; CD // MP (2) (tính chất đường trung bình của tam giác).
Xét tam giác MNQ có: MA = AN; MD = DQ (gt)
=> AD là đường trung bình của tam giác
MNQ => AD = NQ; AD // NQ (tính chất đường trung bình của tam giác).
Từ (1) và (2) suy ra AB = CD; AB // CD
=> ABCD là hình bình hành (dnnb).
Ta có: AB // MP (cmt); NQ ⊥ MP (gt)
=> AB ⊥ NQ. Mặt khác AD // NQ (cmt),
suy ra AD ⊥ AB => = 900
Hình bình hành ABCD có = 900 nên là hình chữ nhật (dhnb).
Diện tích hình thoi MNPQ là:
SMNPQ = MP. NQ (3)
Diện tích hình chữ nhật ABCD là:
SABCD = AB. AD
= MP. NQ
= MP. NQ (4)
Từ (3) và (4) suy ra = .
Bài 11: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 20 cm, OA = 16cm. Diện tích hình thoi ABCD là:
A. 384 cm2
B. 192 cm2
C. 320 cm2
D. 240 cm2
Đáp án: A
Giải thích:
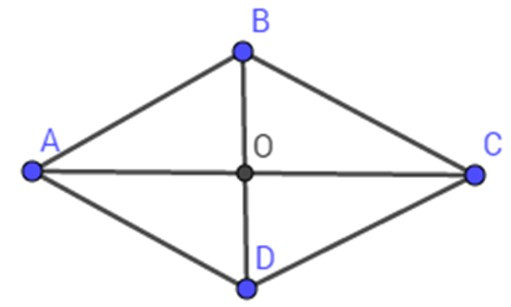
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = = = 12
SABCD = BD. AC = 2OB. 2AO
= 2BO. AO = 2.12.16 = 384 (cm2)
Bài 12: Cho tứ giác ABCD có đường chéo AC vuông góc với BD, diện tích của ABCD là 56 cm2; BD = 7 cm. Độ dài đường chéo AC là:
A. 7 cm
B. 14 cm
C. 8 cm
D. 16 cm
Đáp án: A
Giải thích:
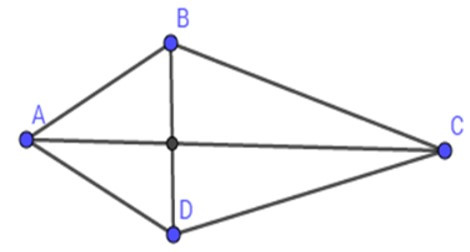
Vì ABCD có đường chéo vuông góc nên
SABCD = BD. AC
=> AC = = = 16 cm.
Bài 13: Cho hình thoi ABCD, khi đó:
A. SABCD = AB. AD
B. SABCD = AC. BD
C. SABCD = AC. BD
D. SABCD = AB2
Đáp án: C
Giải thích:
Hình thoi ABCD có hai đường chéo AC, BD nên diện tích
SABCD = AC. BD.
Bài 14: Cho tứ giác ABCD có đường chéo AC vuông góc với BD, diện tích của ABCD là 25 cm2; BD = 5 cm. Độ dài đường chéo AC là:
A. 10 cm
B. 5 cm
C. 15 cm
D. 12,5 cm
Đáp án: A
Giải thích:
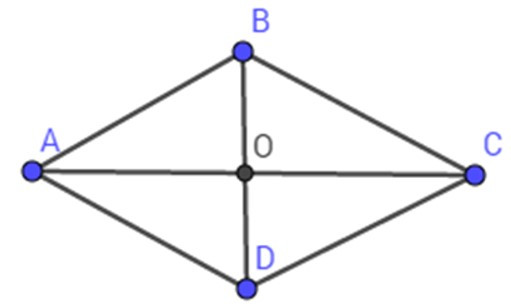
SABCD = BD. AC
=> AC = = = 10 cm.
Bài 15: Cho hình thoi có độ dài hai đường chéo lần lượt là 8cm, 10cm. Diện tích hình thoi là?
A. 80cm2.
B. 40cm2.
C. 18cm2.
D. 9cm2.
Đáp án: B
Giải thích:
Diện tích của hình thoi là S = 1/2d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = 1/2.8.10 = 40( cm2 )
Bài 16: Hình thoi có độ dài hai đường chéo lần lượt là a√ 2 ,cm, a√ 3 cm. Diện tích của hình thoi là ?
A. a2√ 6 ( cm2 )
B. (a2√ 6 )/3( cm2 )
C. (a2√ 6 )/2( cm2 )
D. (a2√ 5 )/2( cm2 )
Đáp án: C
Giải thích:
Diện tích của hình thoi là S = 1/2d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = 1/2. a√ 2 . a√ 3 = (a2√ 6 )/2( cm2 )
Bài 17: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và BACˆ = 600. Diện tích của hình thoi ABCD là ?
A. 8( cm2 )
B. 8√ 3 ( cm2 )
C. 16( cm2 )
D. 16√ 3 ( cm2 )
Đáp án: B
Giải thích:
Xét hình thoi ABCD có BACˆ = 600.
Ta có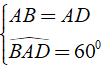
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – to – go ta có:
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2)
⇒ AC = 2AH = 4√ 3 ( cm )
Do đó SABCD = 1/2AC.BD = 1/2.4√ 3 .4 = 8√ 3 ( cm2 )
Chọn đáp án B.
Bài 18: Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là ?
A. 16( cm2 )
B. 8√ 21 ( cm2 )
C. 16√ 21 ( cm2 )
D. 8( cm2 )
Đáp án: C
Giải thích:
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2) = √ (102 - 42) = 2√ 21 ( cm )
⇒ AC = 2AH = 4√ 21 ( cm )
Do đó SABCD = 1/2.BD.AC = 1/2.4√ (21) .8 = 16√ 21 ( cm2 )
Bài 19: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Biết OA = 3cm và OB = 5cm. Tính diện tích hình thoi?
A. 30cm2
B. 35cm2
C. 40cm2
D. 45cm2
Đáp án: A
Giải thích:
VÌ ABCD là hình thoi nên O là trung điểm của AC và BD
Suy ra: AC = 2OA = 2.3 = 6cm
Và BD = 2.OB = 2.5= 10cm
Diện tích hình thoi là:
Chọn đáp án A
Bài 20: Cho hình bình hành ABCD có AB = BC = 10 cm và O là giao điểm của hai đường chéo sao cho OA = 6cm. Tính diện tích hình bình hành ABCD
A. 96
B. 80
C. 72
D. 64
Đáp án: A
Giải thích:
Vì hình bình hành ABCD có 2 cạnh liền kề bằng nhau AB = BC nên ABCD là hình thoi
Suy ra: AB = BC = CD= DA = 10cm và O là trung điểm của AC và trung điểm của BD
Ta có: AC = 2AO = 2. 6 = 12cm
Áp dụng định lí py tago vào tam giác AOD có:
AD2 = AO2 + OD2 suy ra: OD2 = AD2 – AO2 = 102 – 62 = 64 nên OD = 8cm
Suy ra: BD = 2OD = 16cm
Diện tích hình thoi ABCD là:
Chọn đáp án A
Bài 21: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Diện tích của hình thoi là 120cm2; AC = 12cm . Tính độ dài cạnh của hình thoi
A. 2√30cm
B. 2√34cm
C. 8cm
D. 9cm
Đáp án: B
Giải thích:
Diện tích của hình thoi là:
Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD.
Suy ra:
Áp dụng định lí Pytago vào tam giác OAB có:
AB2 = OA2 + OB2 = 62 + 102 = 136
⇒ AB = 2√34cm
Bài 22: Cho hình thoi ABCD có diện tích là 24cm2. Tỉ số độ dài hai đường chéo là 3: 4. Tính độ dài hai đường chéo của hình thoi
A. 9cm và 12cm
B. 12cm và 16cm
C. 6cm và 8cm
D. 3cm và 4cm
Đáp án: C
Giải thích:
Bài 23: Cho hình thoi ABCD có diện tích là 40cm2. Gọi O là giao điểm của hai đường chéo.. Tính diện tích tam giác AOB?
A. 10 cm2
B. 12 cm2
C. 8 cm2
D. 5 cm2
Đáp án: A
Giải thích:
Vì ABCD là hình thoi có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD.
Suy ra
Diện tích hình thoi ABCD là:
Diện tích tam giác vuông OAB là:
Chọn đáp án A
Bài 24: Cho hình thoi ABCD có O là giao điểm của hai đường chéo biết diện tích tam giác ABC là 16cm2. Tính diện tích hình thoi ABCD?
A. 24cm2
B. 32cm2
C. 48cm2
D. 64cm2
Đáp án: B
Giải thích:
Do ABCD là hình thoi nên hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
Diện tích tam giác ABC là
Suy ra: BO.AC = 32
Diện tích hình thoi ABCD là:
Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:
Trắc nghiệm Diện tích đa giác có đáp án
Trắc nghiệm Bài ôn tập Chương 2 có đáp án
Trắc nghiệm Định lý Ta-lét trong tam giác có đáp án
Trắc nghiệm Định lý đảo và hệ quả của định lý Ta-let có đáp án
Trắc nghiệm Tính chất đường phân giác của tam giác có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án