TOP 40 câu Trắc nghiệm Diện tích đa giác (có đáp án 2023) - Toán 8

Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 6: Diện tích đa giác có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 6.

1 1,696 16/02/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 8 Bài 6: Diện tích đa giác

Bài giảng Trắc nghiệm Toán 8 Bài 6: Diện tích đa giác

Bài 1: Cho hình vuông ABCD có cạnh 10m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng $\frac{4}{5}$ diện tích vuông ABCD.

A. Điểm E ở trên cạnh AB sao cho BE = 4 m.

B. Điểm E ở trên cạnh AB sao cho BE = 6 m.

C. Điểm E ở trên cạnh AB sao cho BE = 5 m.

D. Điểm E là trung điểm của AB.

Hiển thị đáp án

Đáp án: B

Giải thích:

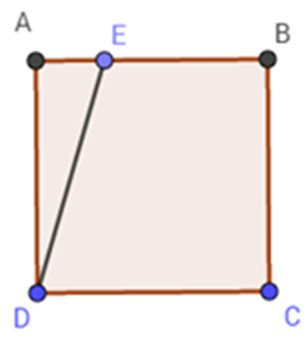
Gọi BE = x (m).

Diện tích hình vuông ABCD là:

S_ABCD = AB² = 10² = 100 (m²)

Diện tích hình than vuông BCDE là:

S_BCDE = $\frac{(B E + D C) B C}{2}$

= $\frac{(x + 10) .10}{2}$ = 5 (x+10)

Vì diện tích hình thang vuông BCDE bằng $\frac{4}{5}$ diện tích hình vuông ABCD nên ta có: S_BCDE = $\frac{4}{5}$ S_ABCD

= 5(x + 10) = $\frac{4}{5}$ .100

$\Leftrightarrow$ x + 10 = 16

$\Leftrightarrow$ x = 6 (m)

Bài 2: Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng diện tích vuông ABCD.

A. Điểm E ở trên cạnh AB sao cho BE = 8 m.

B. Điểm E ở trên cạnh AB sao cho BE = 6 m.

C. Điểm E ở trên cạnh AB sao cho BE = 12 m.

D. Điểm E là trung điểm của AB.

Hiển thị đáp án

Đáp án: D

Giải thích:

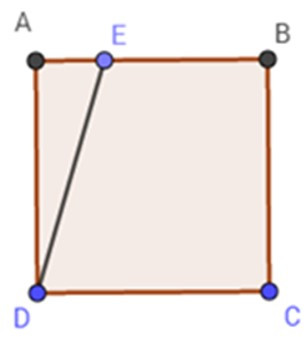
Gọi BE = x (m).

Diện tích hình vuông ABCD là:

S_ABCD = AB² = 20² = 400 (m²)

Diện tích hình than vuông BCDE là:

S_BCDE = $\frac{(B E + D C) B C}{2}$

= $\frac{(x + 20) .20}{2}$ = 10(x + 20)

Vì diện tích hình thang vuông BCDE bằng $\frac{3}{4}$ diện tích hình vuông ABCD nên ta có:

S_BCDE = $\frac{3}{4}$ S_ABCD = 10(x + 20) = $\frac{3}{4}$ .400

$\Leftrightarrow$ x + 20 = 30 $\Leftrightarrow$ x = 10 (m)

Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.

Bài 3: Cho hình bình hành ABCD có = 120⁰, AB = 2BC. Gọi I là trung điểm CD, K là trung điểm của AB. Biết chu vi hình bình hành ABCD bằng 60cm. Tính diện tích hình bình hành ABCD.

A. 100 $\sqrt{3}$ cm²

B. 100cm²

C. 200 $\sqrt{3}$ cm²

D. 200cm²

Hiển thị đáp án

Đáp án: A

Giải thích:

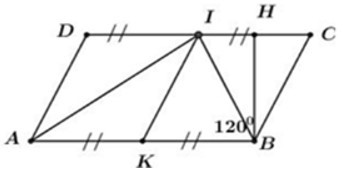
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD

=> S_ABCD = BH.CD

Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.

Trắc nghiệm Diện tích đa giác có đáp án - Toán lớp 8 (ảnh 1)

=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 60⁰).

=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.

=> HI = HC = $\frac{1}{2}$ BC = 5cm

Áp dụng định lý Pytago với tam giác vuông HBC ta có:

$\begin{array}{l} B H = \sqrt{B C^{2} - H C^{2}} \\ = \sqrt{10^{2} - 5^{2}} \\ = \sqrt{75} = 5 \sqrt{3} c m \end{array}$

=> S_ABCD = BH.AB

= BH.2BC = $5 \sqrt{3}$ .2.10

= 100 $\sqrt{3}$ cm²

Bài 4: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC.

Vẽ BP ⊥ MN; CQ ⊥ MN (P, Q Є MN). So sánh S_BPQC và S_ABC.

A. S_ABC = 2S_CBPQ

B. S_ABC < S_CBPQ

C. S_ABC > S_CBPQ

D. S_ABC = S_CBPQ

Hiển thị đáp án

Đáp án: D

Giải thích:

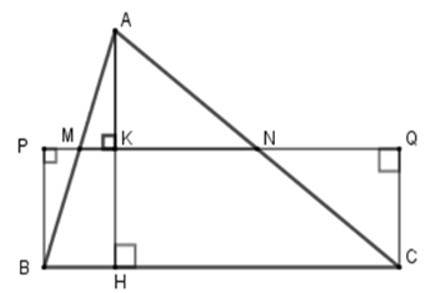
Kẻ AH ⊥ BC tại H và AH cắt MN tại K.

+ Xét tam giác ABC có MN là đường trung bình nên MN // BC suy ra AH ⊥ MN tại K. Xét tứ giác CBPQ

có PQ // BC (do MN // BC) và PB // CQ (do cùng vuông góc với PQ) nên CBPQ là hình bình hành.

Lại có $\hat{P B C}$ = 90⁰ nên tứ giác CBPQ là hình chữ nhật.

Suy ra S_CBPQ = BP. BC.

+ Xét ΔBPM và ΔAKM có:

Suy ra ΔBPM = ΔAKM (ch – gn)

=> BP = AK (hai cạnh tương ứng) (1)

Xét ΔABK có MK // BH (do MN//BC) và M là trung điểm của AB nên K là trung điểm của AH (định lý về đường trung bình của tam giác).

Nên AK = $\frac{1}{2}$ AH (2)

Từ (1) và (2) ta có PB = $\frac{1}{2}$ AH.

+ S_ABC = $\frac{1}{2}$ AH. BC

mà PB = $\frac{1}{2}$ AH (cmt)

nên S_ABC = PB. BC

Lại có S_CBPQ = BP. BC (cmt)

nên ta có S_ABC = S_CBPQ

Bài 5: Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo hai cạnh AM và BN.

A. S_ABC = AM.BN

B. S_ABC = $\frac{3}{2}$ AM.BN

C. S_ABC = $\frac{1}{2}$ AM.BN

D. S_ABC = $\frac{2}{3}$ AM.BN

Hiển thị đáp án

Đáp án: D

Giải thích:

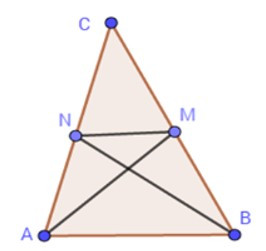
Ta có ABMN là tứ giác có hai đường chéo AM và BN vuông góc nên có diện tích là:

S_ABMN = $\frac{1}{2}$ AB.MN

Hai tam giác AMC và ABC có chung đường cao hạ từ A nên $\frac{S_{A M C}}{S_{A B C}} = \frac{M C}{B C} = \frac{1}{2}$

=> S_AMC = $\frac{1}{2}$ S_ABC (1)

Hai tam giác AMN và AMC có chung đường cao hạ từ M nên $\frac{S_{A M N}}{S_{A M C}} = \frac{A N}{A C} = \frac{1}{2}$

=> S_AMB = $\frac{1}{2}$ S_ABC (2)

Từ (1) và (2) suy ra S_AMN= $\frac{1}{2}$ S_ABC

Hai tam giác AMB và ABC có chung đường cao hạ từ A nên

=> S_AMB = $\frac{1}{2}$ S_ABC

Ta có: S_ABMN= S_AMN + S_ABM

= $\frac{1}{4}$ S_ABC + $\frac{1}{2}$ S_ABC = $\frac{3}{4}$ S_ABC

=> S_ABC = $\frac{4}{3}$ S_ABMN

= $\frac{4}{3} . \frac{1}{2}$ .AM.BN = $\frac{2}{3}$ AM.BN

Bài 6: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ BP ⊥ MN; CQ ⊥ MN (P, Q Є MN). Biết S_ABC = 50 cm², tính S_BPQC.

A. S_BPQC = 50 cm²

B. S_BPQC = 25 cm²

C. S_BPQC = 100 cm²

D. S_BPQC = 75 cm²

Hiển thị đáp án

Đáp án: A

Giải thích:

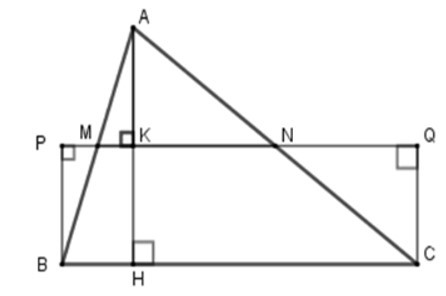
Kẻ AH ⊥ BC tại H và AH cắt MN tại K.

+ Xét tam giác ABC có MN là đường trung bình nên MN // BC suy ra AH ⊥ MN tại K.

Xét tứ giác CBPQ có PQ // BC (do MN // BC) và PB // CQ (do cùng vuông góc với PQ) nên CBPQ là hình bình hành.

Lại có $\hat{P B C}$ = 90⁰ nên tứ giác CBPQ là hình chữ nhật.

Suy ra S_CBPQ = BP. BC.

+ Xét ΔBPM và ΔAKM có:

Suy ra ΔBPM = ΔAKM (ch – gn)

=> BP = AK (hai cạnh tương ứng) (1)

Xét ΔABK có MK // BH (do MN//BC) và M là trung điểm của AB nên K là trung điểm của AH (định lý về đường trung bình của tam giác).

Nên AK = $\frac{1}{2}$ AH (2)

Từ (1) và (2) ta có PB = $\frac{1}{2}$ AH.

+ S_ABC = $\frac{1}{2}$ AH. BC mà

PB = $\frac{1}{2}$ AH (cmt)

nên S_ABC = PB. BC

Lại có S_CBPQ = BP. BC (cmt) nên

ta có S_ABC = S_CBPQ = 50 cm².

Bài 7: Cho tam giác vuông tại ABC. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Biết S_BCHI = 100 cm², tính S_ACFG + S_ABDE

A. S_ACFG + S_ABDE = 200 cm²

B. S_ACFG + S_ABDE = 150 cm²

C. S_ACFG + S_ABDE = 100 cm²

D. S_ACFG + S_ABDE = 180 cm²

Hiển thị đáp án

Đáp án: C

Giải thích:

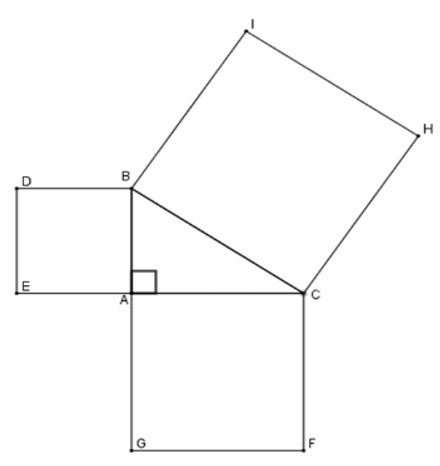
Ta có: S_BCHI = BC²; S_ACFG = AC²; S_ABDE = AB²

Theo định lý Pytago cho tam giác ABC vuông tại A

ta có: BC² = AB² + AC²

=> S_BCHI = S_ACFG + S_ABDE

Vậy S_ACFG + S_ABDE = S_BCHI = 100 cm²

Bài 8: Cho tam giác vuông tại ABC.

Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Chọn khẳng định đúng:

A. S_ACFG = S_BCHI + S_ABDE

B. S_BCHI = S_ACFG + S_ABDE

C. S_ABDE = S_BCHI + S_ACFG

D. S_BCHI = S_ACFG - S_ABDE

Hiển thị đáp án

Đáp án: B

Giải thích:

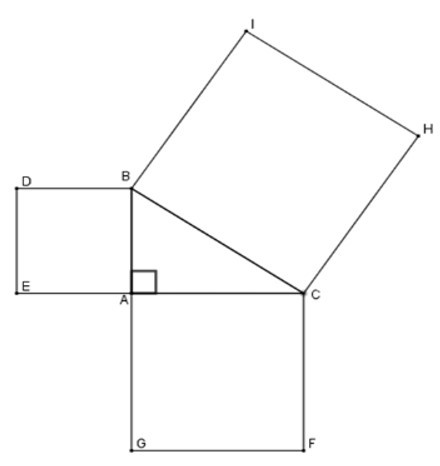
Ta có: S_BCHI = BC²;

S_ACFG = AC²; S_ABDE = AB²

Theo định lý Pytago cho tam giác ABC vuông tại A

ta có: BC² = AB² + AC²

=> S_BCHI = S_ACFG + S_ABDE

Bài 9: Trong các hình thoi có chu vi bằng nahu, hình nào có diện tích lớn nhất?

A. Hình vuông

B. Hình hình hành

C. Hình chữ nhật

D. Hình thoi bất kỳ

Hiển thị đáp án

Đáp án: A

Giải thích:

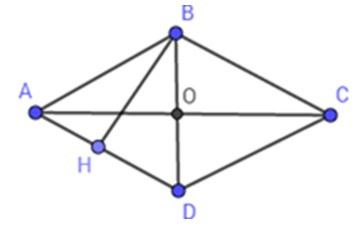
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau.

Kẻ BH vuông góc với AD. Ta có S_ABCD = AD. BH

Trong tam giác vuông ABH vuông tại H thì:

BH ≤ AB (đường vuông góc ngắn hơn đường xiên)

Do đó: S_ABCD = AD. BH ≤ AD. AB

= AB. AB = AB²

S_ABCD có giá tị lớn nhất bằng AB² khi ABCD là hình vuông.

Vây trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.

Bài 10: Cho hình thoi ABCD có BD = 60 cm, AC = 80 cm.

Vẽ các đường cao BE VÀ BF. Tính diện tích tứ giác BEDF.

A. 728 cm²

B. 864 cm²

C. 1278 cm²

D. 1728 cm²

Hiển thị đáp án

Đáp án: D

Giải thích:

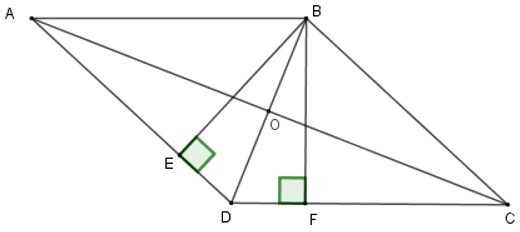
Gọi O là giao điểm của AC, BD.

Vì ABCD là hình thoi nên AC ⊥ BD;

OA = OC = $\frac{A C}{2}$ = 40 cm;

OB = OD = $\frac{B D}{2}$ = 30 cm.

Xét tam giác vuông AOB, theo định lý Pytago ta có:

AB² = OA² + OB²

= 40² + 30² = 2500

=> 50 CM

Lại có:

S_ABCD = $\frac{A C . B D}{2} = \frac{60.80}{2}$ = 2400 cm²

mà S_ABCD = BE. AD

$\Leftrightarrow$ BE.50 = 2400

$\Leftrightarrow$ BE = 48 cm (vì AD = AB = 50 cm)

Xét tam giác vuông BED có:

ED² = BD² – BE²

= 60² – 48² = 1296

=> ED = 36

Suy ra: S_BED = $\frac{1}{2}$ DE. BE

= $\frac{1}{2}$ 48.36 = 864 cm².

Lại có: ΔBED = ΔBFD (ch – gn)

nên S_BFD = S_BED = 864 cm²_.

Từ đó: S_BEDF = S_BFD + S_BED

= 864 + 864 = 1728 cm²

Bài 11: Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A (hình vẽ). Biết S_MNPQ = 484cm². Tính S_ABC.

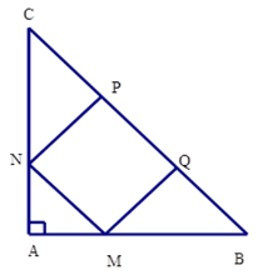
Trắc nghiệm Diện tích đa giác có đáp án - Toán lớp 8 (ảnh 19)

A. 1089cm²

B. 1809cm²

C. $\frac{1089}{2}$ cm²

D. 2178cm²

Hiển thị đáp án

Đáp án: A

Giải thích:

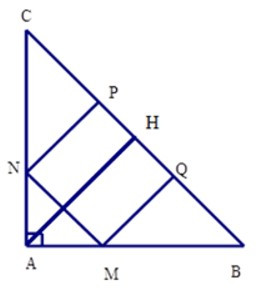
Ta có

Kẻ AH ⊥ BC => H là trung điểm cạnh BC (vì tam giác ABC vuông cân tại A)

Khi đó AH là đường trung tuyến nên

AH = $\frac{B C}{2}$ (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

+ Xét tam giác vuông CNP

có $\hat{C}$ = 45⁰ (do tam giác ABC vuông cân) nên tam giác CNP vuông cân tại P

Suy ra CP =PN = 22cm

+ Tương tự ta có ΔQMB vuông cân tại Q

=> QM = QB = 22cm

Từ đó BC = PC + PQ + QB

= 22 + 22 + 22 = 66cm

Mà AH = $\frac{B C}{2}$ (cmt)

=> AH = $\frac{66}{2}$ = 33cm

Từ đó S_ABC = $\frac{1}{2}$ AH.BC

= $\frac{1}{2}$ .33.66 = 1089 cm²

Bài 12: Cho tam giác ABC có diện tích 12cm². Gọi N là trung điểm của BC, M trên AC

sao cho AM $\frac{1}{3}$ = AC, AN cắt BM tại O.

1. Chọn câu đúng

A. AO = ON

B. BO = 3OM

C. BO = 2OM

D. Cả A, B đều đúng

Hiển thị đáp án

Đáp án: D

Giải thích:

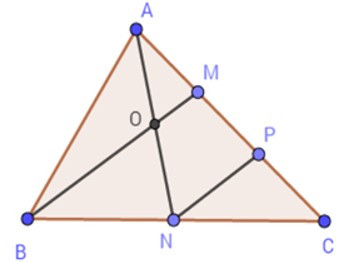
Lấy P là trung điểm của CM.

Vì AM = $\frac{1}{3}$ AC => MC = $\frac{2}{3}$ AC

=> MP = PC = $\frac{1}{3}$ AC = AM

Tam giác BCM có: $\{\begin{cases} N B = N C (g t) \\ P C = P M (g t) \end{cases}$

Suy ra NP là đường trung bình của tam giác BMC (định nghĩa).

Suy ra NP // BM (tính chất đường trung bình).

Tam giác ANP có:

$\{\begin{cases} M A = M P (c m t) \\ O M / / N P (d o N P / / B M) \end{cases}$

=> AO = ON (định lý đảo của đường trung bình).

Theo chứng minh trên ta có OM là đường trung bình của tam giác ANP

nên OM = $\frac{1}{2}$ NP (1)

NP là đường trung bình của tam giác BCM

nên NP = $\frac{1}{2}$ BM (2)

Từ (1) và (2) suy ra BM = 4OM

=> BO = 3OM

Vậy cả A, B đều đúng

Bài 13: Đa giác đều là đa giác ?

A. Có tất cả các cạnh bằng nhau.

B. Có tất cả các góc bằng nhau.

C. Có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

D. Cả 3 đáp án trên đều đúng

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Bài 14: Lục giác đều có?

A. Có 6 cạnh bằng nhau và 6 góc bằng nhau.

B. Có 6 cạnh bằng nhau và 6 góc bất kì

C. Có 5 cạnh bằng nhau và 5 góc bằng nhau.

D. Có 4 cạnh bằng nhau và 4 góc bằng nhau.

Hiển thị đáp án

Đáp án: A

Giải thích:

Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Lục giác đều là đa giác có 6 cạnh và 6 góc bằng nhau.

Bài 15: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?

A. Hình vuông là đa giác đều.

B. Tổng các góc của đa giác lồi 8 cạnh là 1080⁰.

C. Hình thoi là đa giác đều.

D. Số đo góc của hình bát giác đều là 135,5⁰.

Hiển thị đáp án

Đáp án:

Giải thích:

Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau

⇒ Hình vuông là đa giác đều.

⇒ Đáp án A đúng.

+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.

⇒ Hình thoi không phải là đa giác đều.

⇒ Đáp án C sai.

+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).180⁰.

Khi đó tổng các góc của đa giác lồi 8 cạnh là ( 8 - 2 ).180⁰ = 1080⁰.

⇒ Đáp án B đúng.

+ Số đo của một góc của đa giác đều n cạnh là (( n - 2 ).180⁰)/n.

Khi đó số đo của hình bát giác đều là (( 8 - 2 ).180⁰)/8 = 135⁰.

⇒ Đáp án D sai.

Bài 16: Một đa giác 7 cạnh thì số đường chéo của đa giác đó là ?A. 12.

B. 13.

C. 14.

D. Kết quả khác.

Hiển thị đáp án

Đáp án: C

Giải thích:

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2.

Khi đó số đường chéo của đa giác 7 cạnh là (7( 7 - 3 ))/2 = 14 (đường chéo)

Bài 17: Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?

A. 5.

B. 6.

C. 4.

D. 7.

Hiển thị đáp án

Đáp án: A

Giải thích:

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )

Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n² - 3n - 2n = 0

⇔ n² - 5n = 0 ⇔ n( n - 5 ) = 0 ⇔ Bài tập tổng hợp chương 2 Hình học 8 | Lý thuyết và Bài tập Toán 8 có đáp án

So sánh điều kiện ta có n = 5 thỏa mãn.

Chọn đáp án A.

Bài 18: Diện tích hình chữ nhật thay đổi như thế nào nếu chiều rộng tăng 4 lần, chiều dài giảm 2 lần ?

A. Diện tích không đổi

B. Diện tích giảm 2 lần.

C. Diện tích tăng 2 lần.

D. Cả đáp án A, B, C đều sai.

Hiển thị đáp án

Đáp án: C

Giải thích:

Công thức diện tích hình chữ nhật là S_hcn = a.b

Trong đó : a là chiều dài, b là chiều rộng

Theo giả thiết: S_{ban đầu} = a.b

Khi đó ta có: S_sau = 4b.1/2a = 2a.b = 2S_{ban đầu}

Do đó, diện tích sau tăng lên 2 lần.

Bài 19: Cho hình chữ nhật có chiều dài là 4 cm, chiều rộng là 1,5 cm. Diện tích của hình chữ nhật đó là ?

A. 5( cm )

B. 6( cm² )

C. 9( cm )

D. 7( cm² )

Hiển thị đáp án

Đáp án: B

Giải thích:

Công thức diện tích hình chữ nhật là S_hcn = a.b

Trong đó : a là chiều dài, b là chiều rộng

Khi đó ta có: S_hcn = 4. 1,5 = 6( cm² ).

Bài 20: Cho hình vuông có độ dài cạnh hình vuông là 4 cm. Diện tích của hình vuông đó là?

A. 8( cm ).

B. 16( cm )

C. 8( cm² )

D. 16( cm² )

Hiển thị đáp án

Đáp án: D

Giải thích:

Diện tích hình vuông bằng bình phương cạnh của nó: S = a².

Khi đó ta có S_hv = 4.4 = 16 ( cm² ).

Bài 21: Cho tam giác vuông, có độ dài hai cạnh góc vuông lần lượt là 6cm, 4cm. Diện tích của tam giác vuông đó là ?

A. 24( cm² )

B. 14( cm² )

C. 12( cm² )

D. 10( cm² )

Hiển thị đáp án

Đáp án: C

Giải thích:

Diện tích tam giác vuông bằng nửa tích hai cạnh: S = 1/2a.b.

Khi đó ta có S = 1/2. 6. 4 = 12( cm² ).

Bài 22: Cho hình vuông có đường chéo là 6( dm ) thì diện tích là ?

A. 12( cm² )

B. 18( cm² )

C. 20( cm² )

D. 24( cm² )

Hiển thị đáp án

Đáp án: B

Giải thích:

Diện tích hình vuông bằng bình phương cạnh của nó: S = a².

Ngoài công thức này, diện tích hình vuông còn một công thức mở rộng là:

Diện tích hình vuông bằng nửa tích của hai đường chéo

Khi đó ta có : S = 1/2. 6. 6 = 18( cm² ).

Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:

Trắc nghiệm Bài ôn tập Chương 2 có đáp án

Trắc nghiệm Định lý Ta-lét trong tam giác có đáp án

Trắc nghiệm Định lý đảo và hệ quả của định lý Ta-let có đáp án

Trắc nghiệm Tính chất đường phân giác của tam giác có đáp án

Trắc nghiệm Khái niệm về hai tam giác đồng dạng có đáp án

1 1,696 16/02/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3