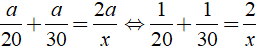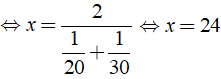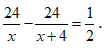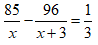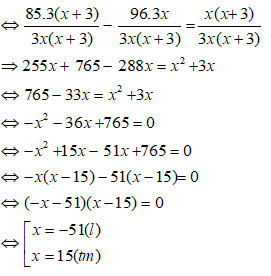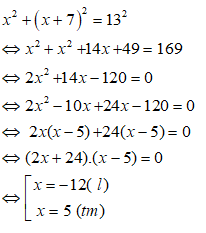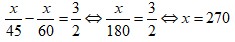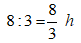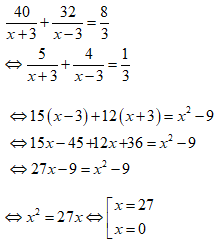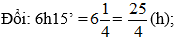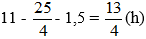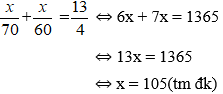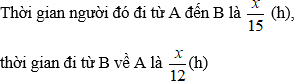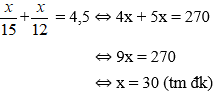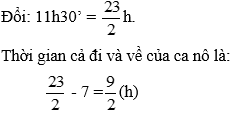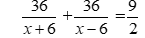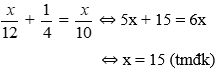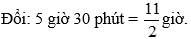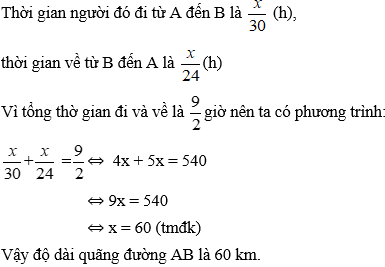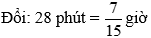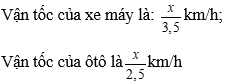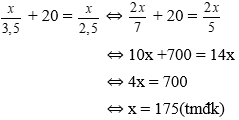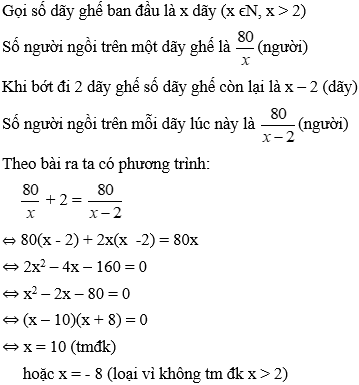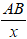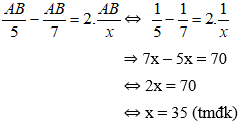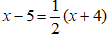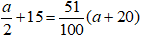TOP 40 câu Trắc nghiệm Giải bài toán bằng cách lập phương trình (có đáp án 2023) - Toán 8
Bộ 40 câu hỏi trắc nghiệm Toán lớp 8 Bài 6: Giải bài toán bằng cách lập phương trình có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 8 Bài 6.
Trắc nghiệm Toán 8 Bài 6: Giải bài toán bằng cách lập phương trình
Bài giảng Trắc nghiệm Toán 8 Bài 6: Giải bài toán bằng cách lập phương trình
Bài 1: Xe thứ hai đi chậm hơn xe thứ nhất 15km/h. Nếu gọi vận tốc xe thứ hai là x (km/h) thì vận tốc xe thứ nhất là:
A. x – 15 (km/h)
B. 15x (km/h)
C. x + 15(km/h)
D. 15 : x (km/h)
Đáp án: C
Giải thích:
Vì xe thứ hai đi chậm hơn xe thứ nhất 15km/h nên vận tốc xe thứ nhất nhiều hơn vận tốc xe thứ hai là 15km/h
Do đó nếu vận tốc xe thứ hai là x (km/h) thì vận tốc xe thứ nhất
là x + 15 (km/h)
Bài 2: Chu vi một mảnh vườn hình chữ nhật là 45m. Biết chiều dài hơn chiều rộng 5m. Nếu gọi chiều rộng mảnh vườn là x (x > 0; m) thì phương trình của bài toán là
A. (2x + 5).2 = 45
B. x + 3
C. 3 – x
D. 3x
Đáp án: A
Giải thích:
Gọi chiều rộng mảnh vườn là x (x > 0; m)
Vì chiều dài hơn chiều rộng 5m nên chiều dài mảnh vườn là x + 5 (m)
Vì chu vi mảnh vườn hình chữ nhật là 45m nên ta có phương trình:
(x + x + 5).2 = 45
2(2x + 5) = 45
Bài 3: Xe tải thứ nhất chở x tấn hàng, xe thứ hai chở gấp đôi xe thứ nhất. Số tấn hàng của xe thứ hai chở được tính theo x là:
A. 2x
B. 2 + x
C. x2
D.
Đáp án: A
Giải thích:
Vì xe thứ hai chở gấp đôi xe thứ nhất nên số tấn hàng của xe thứ hai là 2x (tấn).
Bài 4: Xe máy và ô tô cùng đi trên một con đường, biết vận tốc của xe máy là x (km/h) và mỗi giờ ô tô lại đi nhanh hơn xe máy 20km. Công thức tính vận tốc ô tô là:
A. x – 20 (km/h)
B. 20x (km/h)
C. 20 – x (km/h)
D. 20 + x (km/h)
Đáp án: D
Giải thích:
Mỗi giờ ô tô lại đi nhanh hơn xe máy 20km nghĩa là vận tốc ô tô lớn hơn vận tốc xe máy 20km/h.
Khi đó vận tốc ô tô là x + 20 (km/h)
Bài 5: Một xưởng dệt theo kế hoạch mỗi ngày phải dệt 30 áo. Trong thực tế mỗi ngày xưởng dệt được 40 áo nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn làm thêm đươc 20 chiếc áo nữa. Hãy chọn câu đúng. Nếu gọi thời gian xưởng làm theo kế hoạch là x (ngày, x > 3, x N). Thì phương trình của bài toán là:
A. 40x = 30(x – 3) – 20
B. 40x = 30(x – 3) + 20
C. 30x = 40(x – 3) + 20
D. 30x = 40(x – 3) – 20
Đáp án: D
Giải thích:
Gọi thời gian xưởng làm theo kế hoạch là x (ngày, x > 3, x N)
Tổng số áo theo kế hoạch là 30x (áo)
Vì đội hoàn thành trước thời hạn 3 ngày nên thời gian làm theo thực tế
là x – 3 ngày
Vì theo thực tế đội làm thêm được 20 sản phẩm nên ta có phương trình
40(x – 3) = 30x + 20
40(x – 3) – 20 = 30x.
Bài 6: Số thứ nhất gấp 6 lần số thứ hai. Nếu gọi số thứ nhất là x thì số thứ hai là:
A. 6x
B.
C.
D. x + 6
Đáp án: B
Giải thích:
Vì số thứ nhất gấp 6 lần số thứ hai nên
số thứ hai bằng lần số thứ nhất.
Vậy số thứ nhất là x thì số thứ hai là
Bài 7: Một xưởng dệt theo kế hoạch mỗi ngày phải dệt 30 áo. Trong thực tế mỗi ngày xưởng dệt được 40 áo nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn làm thêm đươc 20 chiếc áo nữa. Hãy chọn câu đúng. Nếu số sản phẩm xưởng cần làm theo kế hoạch là x (sản phẩm, x > 0, x N) thì phương trình của bài toán là:
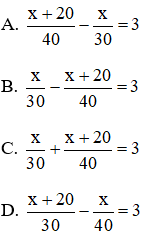
Đáp án: B
Giải thích:
Gọi số sản phẩm xưởng cần làm theo kế hoạch
là x (sản phẩm, x > 0, x N).
Thời gian dự kiến xong là: (ngày)
Vì theo thực tế đội làm được thêm 20 sản phẩm nên số sản phẩm
thực tế làm được là: x + 20 (sản phẩm)
Thời gian thực tế là: (ngày)
Vì đội hoàn thành trước thời hạn 3 ngày nên ta
có phương trình
Bài 8: Một ca nô và một tàu thủy khởi hành cùng một lúc trên một con sông. Biết tàu thủy đến chậm hơn ca nô 3 giờ. Nếu gọi thời gian đi của tàu thủy là x thì thời gian đi của ca nô là:
A. x – 3
B. 3x
C. 3 – x
D. x + 3
Đáp án: A
Giải thích:
Tàu thủy đến chậm hơn ca nô 3 giờ hay thời gian đi của tàu thủy nhiều hơn ca nô là 3 giờ, nghĩa là ca nô đi với thời gian ít hơn tàu thủy 3 giờ.
Thời gian đi của tàu thủy là x thì thời gian đi của ca nô là x – 3 (h)
Bài 9: Hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai 3 giờ. Nếu gọi thời gian đi của xe thứ nhất là x giờ thì thời gian của xe thứ hai là:
A. (x – 3) giờ
B. 3x giờ
C. (3 – x) giờ
D. (x + 3) giờ
Đáp án: D
Giải thích:
Vì hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai 3 giờ nên thời gian xe thứ hai đi nhiều hơn xe thứ nhất 3 giờ.
Nếu thời gian đi của xe thứ nhất là x giờ thì thời gian đi của xe thứ hai là x + 3 giờ.
Bài 10: Một hình chữ nhật có chiều dài là x (cm), chiều dài hơn chiều rộng 3(cm). Diện tích hình chữ nhật là 4 (cm2). Phương trình ẩn x là:
A. 3x = 4
B. (x + 3).3 = 4
C. x(x + 3) = 4
D. x(x – 3) = 4
Đáp án: D
Giải thích:
Vì chiều dài hơn chiều rộng 3 cm nên chiều rộng là x – 3 (cm)
Vì diện tích hình chữ nhật là 4 (cm2)
nên ta có phương trình: x(x – 3) = 4
Bài 11: Một người đi xe máy từ A đến B, với vận tốc 30 km/h. Lúc về người đó đi với vận tốc 24 km/h. Do đó thời gian về lâu hơn thời gian đi là 30 phút. Hãy chọn câu đúng. Nếu gọi thời gian lúc đi là x (giờ, x > 0) thì phương trình của bài toán là:
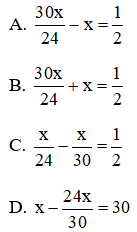
Đáp án: A
Giải thích:
Đổi 30 phút = (h).
Với thời gian lúc đi là x (giờ), quãng đường AB dài là: 30x (km)
Thời gian người đó đi quãng đường AB lúc về là: (h).
Theo đề bài ta có phương trình:
Bài 12: Một công việc được giao cho hai người. Người thứ nhất có thể làm xong công việc một mình trong 24 giờ. Lúc đầu, người thứ nhất làm một mình và sau giờ người thứ hai cùng làm. Hai người làm chung trong giờ thì hoàn thành công việc. Hỏi nếu làm một mình thì người thứ hai cần bao lâu để hoàn thành công việc.
A. 19 giờ
B. 21 giờ
C. 22 giờ
D. 20 giờ
Đáp án: C
Giải thích:
Gọi thời gian làm một mình xong việc của người
thứ hai là x (giờ), điều kiện: x > .
Biểu thị công việc bằng 1 ta có:
Năng suất của người thứ nhất và người thứ hai lần lượt là (công việc/giờ) và (công việc/giờ).
Năng suất làm chung của hai người là (công việc/giờ)
Khối lượng công việc người thứ nhất làm một mình trong giờ là =(công việc)
Khối lượng công việc của hai người làm chung trong giờ là .() (công việc)
Theo bài ra ta có phương trình:
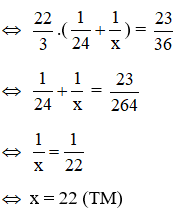
Vậy nếu làm riêng người thứ hai cần làm trong 22 giờ thì xong công việc.
Bài 13: Một người đi xe máy từ A đến B, với vận tốc 30 km/h. Lúc về người đó đi với vận tốc 24 km/h. Do đó thời gian về lâu hơn thời gian đi là 30 phút. Hãy chọn câu đúng. Nếu gọi quãng đường AB là x (km, x > 0) thì phương trình của bài toán là:
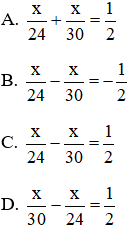
Đáp án: C
Giải thích:
Đổi 30 phút = (h).
Với quãng đường AB là x (km),
thời gian người đó đi hết quãng đường lúc đi là: (h);
thời gian người đó đi quãng đường AB lúc về là: (h).
Theo đề bài ta có phương trình
Bài 14: Một ô tô phải đi quãng đường AB dài 60km trong một thời gian nhất định. Xe đi nửa đầu quãng đường với vận tốc hơn dự định 10km/h và đi với nửa sau kém hơn dự định 6 km/h, Biết ô tô đến đúng dự định. Tính thời gian dự định đi quãng đường AB?
A. 3 giờ
B. 5 giờ
C. 4 giờ
D. 2 giờ
Đáp án: A
Giải thích:
Gọi vận tốc theo dự định của ô tô là x (x > 6) (km/h)
Thời gian theo dự định của ô tô là (h)
Nửa đầu quãng đường ô tô đi với vận tốc là x+10 (km/h)
Thời gian đi nửa đầu quãng đường là (h)
Nửa sau quãng đường, ô tô đi với vận tốc là x − 6 (km/h)
Thời gian ô tô đi nửa sau quãng đường là (h)
Vì ô tô đến nơi đúng dự định nên ta có phương trình
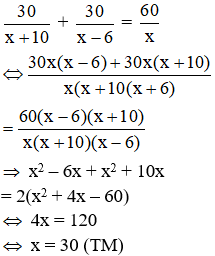
Bài 15: Mẹ hơn con 24 tuổi. Sau 2 năm nữa thì tuổi mẹ gấp 3 lần tuổi con. Tuổi của con hiện nay là:
A. 5.
B. 10.
C. 15.
D. 20.
Đáp án: B
Giải thích:
Gọi số tuổi của con hiện tại là x (Tuổi) (x ∈ N)
→ số tuổi của mẹ là x + 24 (Tuổi)
Theo bài ra ta có: 3(x + 2) = x + 24 + 2
⇔ 3x + 6 = x + 26
⇔ 2x - 20 = 0
⇔ x = 10
Vậy hiện tại tuổi của con là 10 tuổi.
Bài 16: Tìm hai số tự nhiên chẵn liên tiếp biết biết tích của chúng là 24 là:
A. 2;4
B. 4;6
C. 6;8
D. 8;10
Đáp án: B
Giải thích:
Gọi số tuổi của con hiện tại là x (Tuổi) (x ∈ N)
→ số tuổi của mẹ là x + 24 (Tuổi)
Theo bài ra ta có: 3(x + 2) = x + 24 + 2
⇔ 3x + 6 = x + 26
⇔ 2x - 20 = 0
⇔ x = 10
Vậy hiện tại tuổi của con là 10 tuổi.
Bài 17: Một hình chữ nhật có chiều dài hơn chiều rộng 3cm. Chu vi hình chữ nhật là 100cm. Chiều rộng hình chữ nhật là:
A. 23,5cm
B. 47cm
C. 100cm
D. 3cm
Đáp án: A
Giải thích:
Gọi chiều rộng hình chữ nhật là x(cm) (x > 0)
→ Chiều dài hình chữ nhật là x + 3(cm)
Do chu vi hình chữ nhật là 100cm nên ta có:
2[ x + (x + 3) ] = 100 ⇔ 2x + 3 = 50 ⇔ x = 23,5
Vậy chiều rộng hình chữ nhật là 23,5cm
Bài 18: Một xe đạp khởi hành từ điểm A, chạy với vận tốc 15 km/h. Sau đó 6 giờ, một xe hơi đuổi theo với vận tốc 60 km/h. Hỏi xe hơi chạy trong bao lâu thì đuổi kịp xe đạp?
A. 1h
B. 2h
C. 3h
D. 4h
Đáp án: B
Giải thích:
Gọi t ( h ) là thời gian từ lúc xe hơi chạy đến lúc đuổi kịp xe đạp; t > 0.
⇒ t + 6 ( h ) là thời gian kể từ lúc xe đạp đi đến lúc xe hơi đuổi kịp.
+ Quãng đường xe đạp đi được là s1 = 15( t + 6 ) km.
+ Quãng đường xe hơi đi được là s2 = 60t km.
Vì hai xe xuất phát tại điểm A nên khi gặp nhau s1 = s2.
Khi đó ta có: 15(t + 6) = 60t ⇔ 60t - 15t = 90 ⇔ t = 2(h) (thỏa mãn)
Vậy xe hơi chạy được 2 giờ thì đuổi kịp xe đạp.
Bài 19: Một người đi từ A đến B. Trong nửa quãng đường đầu người đó đi với vận tốc 20km/h phần đường còn lại đi với tốc độ 30km/h. Vận tốc trung bình của người đó khi đi từ A đến B là:
A. 20km/h
B. 24km/h
C. 25km/h
D. 30km/h
Đáp án: B
Giải thích:
Gọi vận tốc trung bình của người đó là: x(km/h)
Gọi độ dài nửa quãng đường AB là: a(km)
Khi đó ta có:
+ Thời gian đi nửa quãng đường đầu là: a/20(h)
+ Thời gian đi nửa quãng đường sau là: a/30(h)
→ Thời gian đi cả quãng đường AB là:
Do đó ta có:
Vậy vận tốc cần tìm là 24km/h
Bài 20: Một người đi xe đạp từ A đến B cách nhau 24km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4km/h so với lúc đi, nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A đến B.
A. 12km /h
B. 15km/h
C. 20km/h
D.16km/h
Đáp án: A
Giải thích:
Đổi 30 phút = 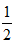
Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x > 0). Thời gian xe đi từ A đến B là 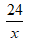
Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là 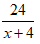
Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:
Giải phương trình:
Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.
Bài 21: Một công nhân theo kế hoạch phải làm 85 sản phẩm trong một khoảng thời gian dự định. Nhưng do yêu cầu đột xuất, người công nhân đó phải làm 96 sản phẩm. Do người công nhân mỗi giờ đã làm tăng thêm 3 sản phẩm nên người đó đã hoàn thành công việc sớm hơn so với thời gian dự định là 20 phút. Tính xem theo dự định mỗi giờ người đó phải làm bao nhiêu sản phẩm, biết rằng mỗi giờ chỉ làm được không quá 20 sản phẩm.
A. 10
B. 12
C. 15
D. 18
Đáp án: C
Giải thích:
Gọi số sản phẩm công nhân dự định làm trong một giờ là x (0 < x ≤ 20).
Thời gian dự kiến người đó làm xong 85 sản phẩm là 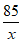
Thực tế mỗi giờ làm tăng thêm 3 sản phẩm nên số sản phẩm làm được mỗi giờ là x + 3.
Do đó 96 sản phẩm được làm trong 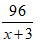
Thời gian hoàn thành công việc thực tế sớm hơn so với dự định là 20 phút = 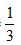
Vậy theo dự định mỗi giờ người đó phải làm 15 sản phẩm.
Bài 22: Một mảnh đất hình chữ nhật có độ dài đường chéo là 13m và chiều dài lớn hơn chiều rộng là 7m. Tính chiều dài của mảnh đất đó.
A. 5m
B. 8m
C. 12m
D. 10m
Đáp án: C
Giải thích:
Gọi chiều rộng của mảnh đất hình chữ nhật là x (m) (0 < x < 13)
Chiều dài mảnh đất hình chữ nhật lớn hơn chiều rộng 7m nên chiều dài của mảnh đất hình chữ nhật là x + 7 (m)
Biết độ dài đường chéo là 13m nên theo định lý Pitago ta có phương trình:
Vậy chiều rộng mảnh đất hình chữ nhật là 5m và chiều dài mảnh đất đó là 12m.
Bài 23: Một ô tô tải đi từ A đến B với vận tốc 45km/h. Sau 1 giờ 30 phút thì một xe con cũng xuất phát đi từ A đến B với vận tốc 60km/h và đến B cùng lúc với xe tải. Tính quãng đường AB.
A. 270 km
B. 200km
C. 240 km
D. 300km
Đáp án: A
Giải thích:
Gọi độ dài quãng đường AB là x (đơn vị km, x > 0)
Thời gian ô tô tải đi từ A đến B là 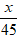
Thời gian xe con đi từ A đến B là 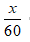
Vì xe con xuất phát sau xe tải 1 giờ 30 phút = 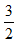
(thỏa mãn điều kiện)
Vậy độ dài quãng đường AB là 270km.
Bài 24: Hai bến sông A và B cách nhau 40km. Cùng một lúc với ca nô xuôi từ bến A có một chiếc bè trôi từ bến A với vận tốc 3km/h. Sau khi đến bến B, ca nô quay trở về bến A ngay và gặp bè, khi đó bè đã trôi được 8km. Tính vận tốc riêng của ca nô.
A. 20km/h
B. 25km/h
C. 27 km /h
D. 30km/h
Đáp án: C
Giải thích:
Gọi vận tốc ca nô là x(km/h), x > 3. Vận tốc ca nô xuôi dòng là x + 3(km/h)
Thời gian ca nô xuôi dòng từ A đến B là 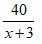
Vận tốc ca nô ngược dòng là x - 3 (km/h)
Quãng đường ca nô ngược dòng từ B đến địa điểm gặp bè là : 40 - 8 = 32 km
Thời gian ca nô ngược dòng từ B đến địa điểm gặp bè là: 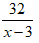
Thời gian bè trôi là:
Ta có phương trình:
So sánh với điều kiện thì chỉ có nghiệm x = 27 thỏa mãn, suy ra vận tốc của ca nô là 27km/h.
Bài 25: Một xe vận tải đi từ địa điểm A đến địa điểm B với vận tốc 50 km/h, rồi từ B quay ngay về A với vận tốc 40 km/h. Cả đi và về mất một thời gian là 5 giờ 24 phút. Tìm chiều dài quãng đường từ A đến B.
A. 80km
B. 120km
C. 216km
D. 30km
Đáp án: B
Giải thích:
Bài 26: Một xe đạp khởi hành từ điểm A, chạy với vận tốc 20 km/h. Sau đó 3 giờ, một xe hơi đuổi theo với vận tốc 50 km/h. Hỏi xe hơi chạy trong bao lâu thì đuổi kịp xe đạp?
A. 2h
B. 4h
C. 3h
D. 1h
Đáp án: A
Giải thích:
Gọi thời gian xe hơi bắt đầu chạy đến khi gặp xe đạp là x giờ (x > 0)
Thời gian xe đạp đi đến khi gặp xe hơi là x + 3 (h)
Quãng đường xe hơi đi được là 50x(km), quãng đường xe đạp đi được là 20(x + 3) (km)
Vì cả hai xe cùng đi từ A đến khi gặp nhau thì quãng đường hai xe đi được là bằng nhau nên ta có phương trình:
50x = 20(x + 3)
⇔ 50x = 20x + 60
⇔ 30x = 60
⇔ x = 2 (tm đk)
Vậy xe hơi chạy trong 2 giờ sẽ đuổi kịp xe đạp
Bài 27: Lúc 6 giờ 15 phút, một ô tô đi từ A để đến B với vận tốc 70 km/h. Khi đến B, ô tô nghỉ 1 giờ rưỡi, rồi quay về A với vận tốc 60 km/h và đến A lúc 11 giờ cùng ngày. Tính quãng đường AB.
A. 100km.
B. 125km.
C. 105km.
D. 110km.
Đáp án: C
Giải thích:
Tổng thời gian xe ô tô đi từ A đến B và đi từ B về A (không tính thời gian nghỉ) là:
Gọi độ dài quãng đường AB là x km (x > 0)
Thời gian xe ô tô đi từ A đên B là 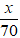
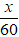
Tổng thời gian đi của xe là 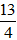
Vậy độ dài quãng đường AB là 105km.
Bài 28: Một người đi xe đạp từ địa điểm A đến địa điểm B với vận tốc 15km/h và sau đó quay trở về từ B đến A với vận tốc 12km/h. Cả đi lẫn về mất 4 giờ 30 phút. Tính chiều dài quãng đường.
A. 40km.
B. 30km.
C. 50km.
D. 60km.
Đáp án: A
Giải thích:
Đổi 4h30’ = 4,5h
Gọi độ dài quãng đường AB là x km (x > 0)
Tổng thời gian đi của xe đạp là 4,5 giờ nên ta có phương trình:
Vậy độ dài quãng đường AB là 30km.
Bài 29: Lúc 7 giờ. Một ca nô xuôi dòng từ A đến B cách nhau 36km rồi ngay lập tức quay về bên A lúc 11 giờ 30 phút. Tính vận tốc của ca nô khi xuôi dòng. Biết rằng vận tốc nước chảy là 6km/h.
A. 18 km/h
B. 24 km/h
C. 8 km/h
D. 12 km/h
Đáp án: B
Giải thích:
Gọi vận tốc riêng của ca nô khi nước lặng yên là x (km/h) (x > 6)
Vận tốc của ca nô khi xuôi dòng là x + 6 (km/h)
Vận tốc của ca nô khi ngược dòng là x - 6(km/h)
Vì tổng thời gian cả đi và về là 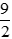
⇒ 36(x – 6).2 + 36(x + 6).2 = 9(x + 6)(x – 6)
⇔ 72x – 72.6+ 72x + 72.6 = 9x2 - 9.36
⇔ 9x2 – 144x – 9.36 = 0
⇔ x2 – 16x – 36 = 0
⇔ (x + 2)(x – 18) = 0
⇔ x + 2 = 0 hoặc x – 18 = 0
⇔ x = -2 hoặc x = 18
Vì x = - 2 không TMĐK x > 6 nên vận tốc riêng của ca nô là 18km/h.
Vậy vận tốc của ca nô khi xuôi dòng là 18 + 6 = 24 km/h
Bài 30: Một ca nô xuôi dòng từ bến A đến bến B mất 4 giờ, và ngược dòng từ bến B đến bến A mất 5h. Tính khoảng cách giữa hai bến, biết vận tốc dòng nước là 2 km/h.
A. 80 km
B. 20 km
C. 72 km
D. 144 km
Đáp án: A
Giải thích:
Gọi vận tốc riêng của ca nô là x km/h(x > 2)
Vận tốc của ca nô khi xuôi dòng là x + 2 (km/h)
Vận tốc của ca nô khi ngược dòng là x - 2(km/h)
Quãng đường khi xuôi dòng của ca nô là 4(x + 2)(km). quãng đường khi ngược dòng của ca nô là 5(x – 2)(km)
Vì quãng đường đi của ca nô khi xuôi dòng và khi ngược dòng là như nhau nên ta có phương trình:
4(x + 2) = 5(x – 2)
⇔ 4x + 8 = 5x - 10
⇔ x = 18 (tmđk)
Vậy khoảng cách giữa hai bến A và B là 4(18 + 2) = 80km.
Bài 31: Một người đi xe đạp từ A đến B với vận tốc trung bình 12km/h. Khi đi về từ B đến A. Người đó đi với vận tốc trung bình là 10 km/h, nên thời gian về nhiều hơn thời gian đi là 15 phút. Tính độ dài quãng đường AB.
A. 15 km
B. 20 km
C. 30 km
D. 80 km
Đáp án: A
Giải thích:
Vì thời gian về nhiều hơn thời gian đi là 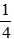
Vậy độ dài quãng đường AB là 15km
Bài 32: Một người đi xe máy từ A đến B với vận tốc 30 km/h. Đến B người đó làm việc trong một giờ rồi quay về A với vận tốc 24 km/h. Biết thời gian tổng cộng hết 5 giờ 30 phút. Tính quãng đường AB.
A. 40 km
B. 20 km
C. 60 km
D. 80 km
Đáp án: C
Giải thích:
Tổng thời gian xe đi từ A đến B và đi từ B về A (không tính thời gian làm việc tại B) là: 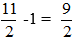
Gọi độ dài quãng đường AB là x km (x >0)
Bài 33: Một bạn học sinh đi học từ nhà đến trường với vận tốc trung bình 4 km/h. Sau khi đi được 2/3 quãng đường bạn ấy đã tăng vận tốc lên 5 km/h. Tính quãng đường từ nhà đến trường của bạn học sinh đó, biết rằng thời gian bạn ấy đi từ nhà đến trường là 28 phút.
A. 4 km
B. 20 km
C. 3 km
D. 6 km
Đáp án: A
Giải thích:
Gọi quãng đường từ nhà đến trường của bạn học sinh là x km(x > 0)
Bài 34: Tổng số tuổi của An và bố hiện nay là 54. Biết rằng bố sinh An khi bố 30 tuổi. Tính tuổi An hiện nay?
Đáp án: A
Giải thích:
Gọi tuổi của An hiện nay là x (0 < x < 24)
Tuổi của bố An hiện nay là x + 30
Vì tổng số tuổi của An và bố là 54 nên ta có phương trình:
x + x + 30 = 54 ⇔ 2x = 24 ⇔ x = 12 (tmđk)
Vậy năm nay An 12 tuổi
Bài 35: Một người đi từ A đến B, nếu đi bằng xe máy thì mất thời gian là 3 giờ 30 phút, còn đi bằng ô tô thì mất thời gian là 2 giờ 30 phút. Tính quãng đường AB, biết rằng vận tốc ôtô lớn hơn vận tốc xe máy là 20 km/h.
A. 180km.
B. 200km.
C. 100km.
D. 175km.
Đáp án: D
Giải thích:
Đổi: 3 giờ 30 phút = 3,5 giờ; 2 giờ 30 phút = 2,5 giờ.
Gọi độ dài quãng đường AB là x km (x >0)
Vì vận tốc ôtô lớn hơn vận tốc xe máy là 20 km/h nên ta có phương trình:
Vậy độ dài quãng đường AB là 175km.
Bài 36: Trong một phòng họp có 80 người ngồi họp được xếp đều ngồi trên các dãy ghế. Nếu ta bớt đi 2 dãy thì mỗi dãy còn lại phải xếp thêm 2 người mới đủ chỗ. Hỏi lúc đầu có bao nhiêu dãy ghế?
A. 10 dãy.
B. 8 dãy.
C. 6 dãy.
D, 12 dãy.
Đáp án: A
Giải thích:
Vậy số dãy ghế ban đầu là 10 dãy.
Bài 37: Trong một buổi họp mặt giữa hai lớp 8A và 8B, có tất cả 50 học sinh tham gia. Các bạn lớp 8B tính số người quen ở lớp 8A và thấy rằng bạn Anh quen 11 bạn, bạn Bắc quen 12 bạn, bạn Châu quen 13 bạn,…và cứ như vậy đến bạn cuối cùng là bạn Yến quen tất cả các bạn của lớp 8A. Tính số học sinh lớp 8B tham gia họp mặt.
A. 10 học sinh
B. 50 học sinh
C. 20 học sinh
D. 30 học sinh
Đáp án: D
Giải thích:
Gọi số học sinh lớp 8B là x bạn (x ∈ N, 0 ≤ x ≤ 50)
Bạn thứ nhất của lớp 8B (bạn Anh) quen 10 + 1 bạn của lớp 8A.
Bạn thứ hai của lớp 8B (bạn Bắc) quen 10 + 2 bạn của lớp 8A.
Bạn thứ ba của lớp 8B (bạn Châu) quen 10 + 3 bạn của lớp 8A.
…………………
Bạn thứ x của lớp 8B (bạn Yến) quen 10 + x bạn của lớp 8A. Mà bạn Yến quen tất cả các bạn lớp 8A nên số học sinh lớp 8A tham gia họp mặt là 10 + x.
Vì có tất cả 50 học sinh tham gia họp mặt nên ta có phương trình:
x + 10 + x = 50 ⇔ 2x = 40 ⇔ x = 20 (tm đk)
Vậy lớp 8A có 20 học sinh, lớp 8B có 30 học sinh dự họp mặt.
Bài 38: Một chiếc thuyền đi xuôi dòng từ bến A đến bến B hết 5 giờ, ngược dòng từ bến B về bến A hết 7 giờ. Hỏi một đám bèo trôi theo dòng sông từ A đến B hết bao lâu?
A. 17,5 giờ
B. 35 giờ
C. 30 giờ
D. 25 giờ
Đáp án: B
Giải thích:
Ta có vận tốc trôi của đám bèo chính là vận tốc của dòng nước.
Gọi thời gian cụm bèo trôi từ bến A về bến B là x giờ (x > 0).
Quãng đường đi từ bến A đến bến B là AB
Vận tốc cụm bèo trôi hay chính là vận tốc chảy của dòng nước là
Vì vận tốc của thuyền khi xuôi dòng bằng tổng vận tốc thực của thuyền và vận tốc dòng nước. Vận tốc của thuyền khi ngược dòng bằng hiệu vận tốc thực của thuyền và vận tốc dòng nước. Do đó hiệu vận tốc lúc xuôi dòng và lúc ngược dòng của chiếc thuyền bằng hai lần vận tốc dòng nước.
Từ đó ta có phương trình:
Vậy thời gian cụm bèo trôi từ bến A về bến B là 35 giờ.
Bài 39: Trước đây 5 năm, tuổi Dung bằng nửa tuổi của Dung sau 4 năm nữa. Tính tuổi của Dung hiện nay?
Đáp án: B
Giải thích:
Gọi số tuổi của Dung năm nay là x (x ∈ N, x > 5)
Năm năm trước tuổi Dung là x – 5.
Bốn năm nữa, tuổi Dung là x + 4.
Vì số tuổi 5 năm trước bằng nửa tuổi của Dung 4 năm sau nên ta có phương trình
⇔ 2(x – 5) = x + 4
⇔ 2x – 10 = x + 4
⇔ x = 14 (tmđk)
Vậy năm nay Dung 14 tuổi.
Bài 40: Trong một trường học, vào đầu năm học số học sinh nam và nữ bằng nhau. Nhưng trong học kì 1, trường nhận thêm 15 học sinh nữ và 5 học sinh nam nên số học sinh nữ chiếm 51% số học sinh của trường. Hỏi cuối học kì 1, trường có bao nhiêu học sinh nam, học sinh nữ?
Đáp án: D
Giải thích:
Gọi số học sinh toàn trường đầu năm học là a học sinh (a ∈ N*)
Số học sinh nữ đầu năm học là a/ 2 học sinh.
Khi nhà trường nhận thêm 15 học sinh nữ và 5 học sinh nam thì số học sinh nữ là a/2 + 15 và số học sinh toàn trường là a + 20 học sinh.
Vì số học sinh nữ lúc này chiếm 51% số học sinh toàn trường nên ta có phương trình:
⇔ 50a + 1500 = 51a + 1020
⇔ a = 480 (thỏa mãn điều kiện a ∈ N*)
Vậy đến cuối kì I số học sinh nữ trong trường là 480: 2 + 15 = 255 học sinh, số học sinh nam là 480: 2 + 5 = 245 học sinh.
Các câu hỏi trắc nghiệm Toán lớp 8 có đáp án, chọn lọc khác:
Trắc nghiệm Giải bài toán bằng cách lập phương trình (tiếp theo) có đáp án
Trắc nghiệm Bài ôn tập Chương 3 có đáp án
Trắc nghiệm Liên hệ giữa thứ tự và phép cộng có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án