Nội dung bài viết

    Xem thêm

    Chuyên đề Diện tích tam giác (2022) - Toán 8

    Với Chuyên đề Diện tích tam giác(2022) - Toán 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.

    1 971 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Chuyên đề Diện tích tam giác - Toán 8

    A. Lý thuyết

    1. Định lý

    Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

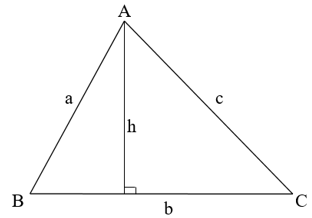
    Lý thuyết: Diện tích tam giác

    Ta có: S = 1/2b.h.

    Ví dụ: Cho tam giác Δ ABC có độ dài đường cao h = 4 cm, đáy BC = 5 cm. Tính diện tích Δ ABC?

    Hướng dẫn:

    Diện tích của tam giác Δ ABC là SABC = 1/2BC.h = 1/24.5 = 10cm2.

    2. Hệ quả

    Nếu Δ ABC vuông (áp dụng với hình bên trên) thì diện tích của tam giác bằng một nửa của tích hai cạnh góc vuông.

    Tổng quát : S = 12a.c (áp dụng với kí hiệu ở hình trên).

    Ví dụ: Cho Δ ABC vuông tại A có cạnh AB = 3 cm;AC = 4 cm. Tính diện tích của tam giác Δ ABC?

    Hướng dẫn:

    Diện tích của tam giác ABC là SABC = 1/2AB.AC = 1/2.3.4 = 6cm2

    B. Trắc nghiệm & Tự luận

    I. Bài tập trắc nghiệm

    Bài 1: Cho Δ ABC, có đường cao AH = 2/3BC thì diện tích tam giác là?

    A. 2/5BC2.

    B. 2/3BC2.

    C. 1/3BC2.

    D. 1/3BC.

    Ta có diện tích của tam giác: S = 1/2b.h.

    Trong đó: b là độ dài cạnh đáy, h là độ dài đường cao

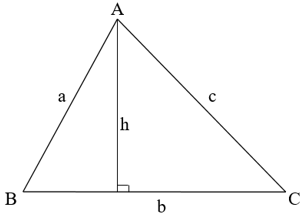
    Bài tập: Diện tích tam giác

    Khi đó ta có : S = 1/2AH.BC = 1/2.2/3BC.BC = 1/3BC2.

    Chọn đáp án C.

    Bài 2: Δ ABC có đáy BC = 6cm, đường cao AH = 4cm. Diện tích Δ ABC là?

    A. 24cm2

    B. 12cm2

    C. 24cm.

    D. 14cm2

    Ta có diện tích Δ ABC là S = 1/2AH.BC = 1/2.6.4 = 12cm2.Chọn đáp án B.

    Bài 3: Cho Δ ABC vuông tại A, có đáy BC = 5cm và AB = 4cm. Diện tích Δ ABC là?

    A. 12cm2

    B. 10cm

    C. 6cm2

    D. 3cm2

    Áp dụng định lý Py – to – go ta có: AB2 + AC2 = BC2

    ⇒ AC = √ (BC2 - AB2)

    ⇒ AC = √ (52 - 42) = 3cm.

    Khi đó SABC = 1/2AB.AC = 1/2.4.3 = 6cm2

    Chọn đáp án C.

    Bài 4: Cho Δ ABC, đường cao AH. Biết AB = 15cm, AC = 41cm, HB = 12cm. Diện tích của Δ ABC là?

    A. 234cm2

    B. 214cm2

    C. 200cm2

    D. 154cm2

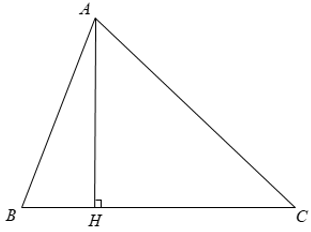
    Bài tập: Diện tích tam giác

    Áp dụng định lý Py – to – go ta có:

    + Xét Δ ABH có AH2 + BH2 = AB2 ⇒ AH = √ (AB2 - BH2)

    ⇒ AH = √ (152 - 122) = 9 (cm).+

    Xét Δ ACH có AC2 = AH2 + HC2 

    ⇒ HC = √ (AC2 - AH2)

    ⇒ HC = √ (412 - 92) = 40 (cm).

    Khi đó SABC = 1/2AH.BC = 1/2AH( HB + HC )

    = 1/2.9.(12 + 40) = 234 (cm2 ).

    Chọn đáp án A.

    II. Bài tập tự luận

    Bài 1: Tính diện tích của một tam giác cân có cạnh đáy là a, cạnh bên bằng b. Từ đó hãy tính diện tích của một tam giác đều có cạnh bằng a.

    Hướng dẫn:

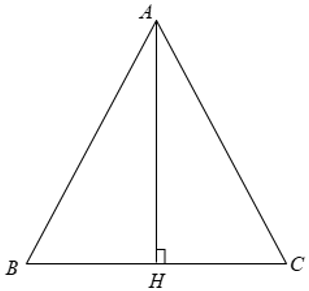
    Bài tập: Diện tích tam giác

    Xét Δ ABC cân tại A có AB = AC = b, BC = a.

    Từ A kẻ AH ⊥ BC.

    Ta có BH = HC = 1/2BC = a/2

    Khi đó ta có: SABC = 1/2AH.BC = 1/2.a.AH

    Áp dụng định lý Py – to – go ta có:

    AC2 = AH2 + HC2 ⇒ AH = √ (AC2 - HC2) .

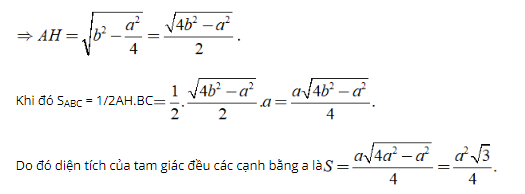
    Bài tập: Diện tích tam giác

    Bài 2: Cho Δ ABC cân tại A có BC = 30cm, đường cao AH = 20cm. Tính đường cao ứng với cạnh bên của tam giác cân đó.

    Hướng dẫn:

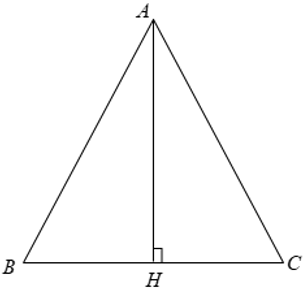
    Bài tập: Diện tích tam giác

    Xét Δ ABC cân tại A có BC = 30cm

    ⇒ BH = CH = 15cm

    Áp dụng đinh lý Py – ta – go ta có:

    AB = √ (AH2 + HB2) = √ (202 + 152) = 25cm

    Kẻ BK ⊥ AC, giờ ta phải tính BK = ?

    Ta có : SABC = 1/2AH.BC = 1/2.20.30 = 300 cm2

    Mặt khác SABC = 1/2BK.AC = 1/2.BK.25

    Do đó, ta có 1/2BK.25 = 300 ⇔ BK = (2.300)/25 = 24cm

    Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:

    Chuyên đề Đa giác. Đa giác đều

    Chuyên đề Diện tích hình chữ nhật

    Chuyên đề Diện tích hình thang

    Chuyên đề Diện tích hình thoi

    Chuyên đề Diện tích đa giác

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 971 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: