Chuyên đề Hình vuông (2022) - Toán 8
Chuyên đề Hình vuông - Toán 8
A. Lý thuyết
1. Định nghĩa
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
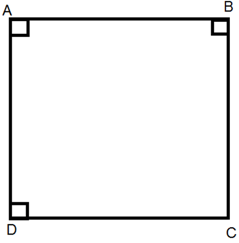
Tổng quát: ABCD là hình vuông ⇔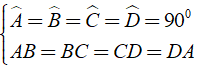
Nhận xét:
+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
+ Hình vuông là hình thoi có bốn góc vuông.
+ Hình vuông vừa là hình chữ nhật vừa là hình thoi.
2. Tính chất
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
3. Dấu hiệu nhận biết hình vuông
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
Ví dụ: Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.
Hướng dẫn:
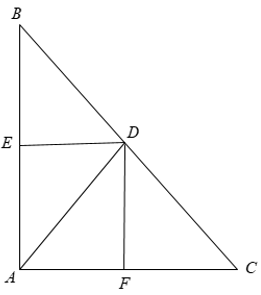
+ Xét tứ giác AEDF có ˆA=ˆE=ˆFˆ = 900
⇒ AEDF là hình chữ nhật . (1)
Theo giả thiết ta có AD là đường phân giác của ˆAˆ
⇒ ^EADˆ = ^DAFˆ = 450.
+ Xét Δ AED có ^AED = 900; ^DAE = 450 ⇒ ^EDAˆ = 450
⇒ Δ AED vuông cân tại E nên AE = ED (2)
Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông (dấu hiệu 1 – mục 3)
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Hãy khoanh tròn vào phương án đúng nhất trong các phương án sau?
A. Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
B. Hình vuông là tứ giác có 4 góc bằng nhau.
C. Hình vuông là tứ giác có 4 cạnh bằng nhau.
D. Hình vuông là tứ giác có hai cạnh kề bằng nhau.
+ Tứ giác có 4 góc vuông là hình chữ nhật
Hình chữ nhật có 4 cạnh bằng nhau là hình vuông.
⇒ Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.Chọn đáp án A.
Bài 2: Hãy chọn đáp án sai trong các phương án sau đây?
A. Trong hình vuông có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
B. Trong hình vuông có hai đường chéo không vuông góc với nhau.
C. Trong hình vuông thì hai đường chéo đồng thời là hai trục đối xứng của hình vuông.
D. Trong hình vuông có hai đường chéo vuông góc với nhau và bằng nhau.
+ Trong hình vuông có hai đường chéo vuông góc với nhau, bằng nhau và cắt nhau tại trung điểm mỗi đường
+ Hai đường chéo trong hình vuông đồng thời là trục đối xứng của hình vuông đó.→ Đáp án B sai.Chọn đáp án B.
Bài 3: Trong các dấu hiệu nhận biết sau thì dấu hiệu nào không đủ điều kiện để tứ giác là hình vuông?
A. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
B. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
C. Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
D. Hình bình hành có hai đường chéo bằng nhau là hình vuông.
Dấu hiệu nhận biết hình vuông:
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.→ Hình bình hành có hai đường chéo bằng nhau thì không là hình vuông.→ Đáp án D sai.Chọn đáp án D.
Bài 4: Tìm câu nói đúng khi nói về hình vuông?
A. Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
B. Hình thoi có một góc vuông là hình vuông.
C. Hình thoi có hai đường chéo bằng nhau là hình vuông.
D. Các phương án đều đúng.
Dấu hiệu nhận biết hình vuông:
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.⇒ Hình vuông vừa là hình chữ nhật, cũng vừa là hình thoi.⇒ Cả 3 phương án đều đúng.Chọn đáp án D.
Bài 5: Một hình vuông có độ dài cạnh bằng 4cm thì độ dài đường chéo của hình vuông là?
A. 8cm
B. √ 32 cm
C. 5cm
D. 4cm
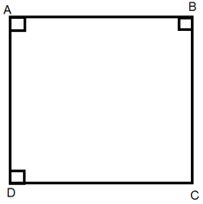
Hình vuông có độ dài cạnh là a (cm)
Áp dụng định lý Py – to – go thì độ dài đường chéo của hình vuông là a√ 2 cm
Do đó với a = 4 thì độ dài đường chéo là 4√ 2 = √ 32 ( cm )
Chọn đáp án B.
II. Bài tập tự luận
Bài 1: Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
Hướng dẫn:
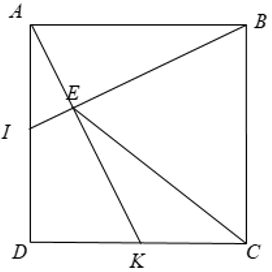
Xét Δ BAI và Δ ADK có: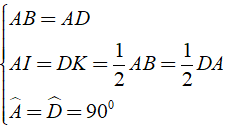
⇒ Δ BAI = Δ ADK (c - g - c)
⇒ ^ABI= ^DAK (góc tương ứng bằng nhau)
Mà IAEˆ + EABˆ = 900 ⇒ ABIˆ + EABˆ = 900
+ Xét Δ ABE có EABˆ + ABEˆ + AEBˆ = 1800
⇒ AEBˆ = 1800 - (ABEˆ + BAEˆ) = 1800 - 900 = 900 hay AK ⊥ BI (đpcm)
+ Xét tứ giác EBCK có KEBˆ + EBCˆ + BCKˆ+ CKEˆ = 3600
⇒ EBCˆ + EKCˆ = 1800.
Mà AKDˆ + AKCˆ = 1800 nên EBCˆ = EKDˆ
+ Tứ giác EBCK nội tiếp nên BECˆ = BKCˆ
Mà BKCˆ = AKDˆ nên EBCˆ = BECˆ hay tam giác BEC cân tại C
⇒ CE = BC = AB (đpcm)
Bài 2: Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho MANˆ = 450. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính :
a) Tính số đo KANˆ = ?
b) Chu vi tam giác MCN theo a.
Hướng dẫn:
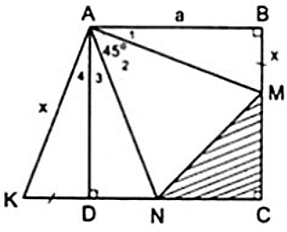
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
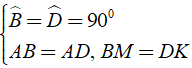
⇒ Δ ABM = Δ ADK (c - g - c)
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
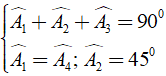
⇒ ^KANˆ = ^A3+ ^A4ˆ = ^A1 + ^A3 = 900 - 450 = 450
b) Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
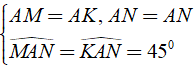
⇒ Δ AMN = Δ AKN (c - g - c)
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.
Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:
Chuyên đề Đường thẳng song song với một đường thẳng cho trước
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
