Nội dung bài viết

    Xem thêm

    Chuyên đề Bất phương trình bậc nhất một ẩn (2022) - Toán 8

    Với Chuyên đề Bất phương trình bậc nhất một ẩn (2022) - Toán 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.

    1 1,409 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Chuyên đề Bất phương trình bậc nhất một ẩn - Toán 8

    A. Lý thuyết

    1. Định nghĩa

    Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b < 0, ax + b ≤ 0, ax + b ≥ 0 ) trong đó a và b là hai số đã cho, a \ne 0 , được gọi là bất phương trình bậc nhất một ẩn.

    Ví dụ:

    Các bất phương trình bậc nhất một ẩn như: 2x + 3 > 0; 3 - x ≤ 0; x + 2 < 0; 4x + 7 ≥ 0; ...

    2. Hai quy tắc biến đổi bất phương trình

    a) Quy tắc chuyển vế

    Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.

    Ví dụ: Giải bất phương trình x - 3 < 4.

    Hướng dẫn:

    Ta có x - 3 < 4

    ⇔ x < 4 + 3 (chuyển vế - 3 và đổi dấu thành 3)

    ⇔ x < 7.

    Vậy tập nghiệm của bất phương trình là { x| x < 7 }.

    b) Quy tắc nhân với một số.

    Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:

    Giữ nguyên chiều bất phương trình nếu số đó dương.

    Đổi chiều bất phương trình nếu số đó âm.

    Ví dụ 1: Giải bất phương trình (x - 1)/3 ≥ 2.

    Hướng dẫn:

    Ta có: (x - 1)/3 ≥ 2

    ⇔ (x - 1)/3.3 ≥ 2.3 (nhân cả hai vế với 3)

    ⇔ x - 1 ≥ 6 ⇔ x ≥ 7.

    Vậy tập nghiệm của bất phương trình là { x| x ≥ 7 }.

    Ví dụ 2: Giải bất phương trình 1 - 2/3x ≤ - 1.

    Hướng dẫn:

    Ta có: 1 - 2/3x ≤ - 1 ⇔ - 2/3x ≤ - 2

    ⇔ - 2/3x.( - 3 ) ≥ ( - 2 )( - 3 ) (nhân cả hai vế với - 3 và đổi dấu)

    ⇔ 2x ≥ 6 ⇔ x ≥ 3.

    Vậy bất phương trình có tập nghiệm là { x| x ≥ 3 }.

    3. Giải bất phương trình bậc nhất một ẩn

    Áp dụng hai quy tắc biến đổi trên, ta giải bất phương trình bậc nhất một ẩn như sau:

    Dạng ax + b > 0 ⇔ ax > - b

    ⇔ x > - b/a nếu a > 0 hoặc x < - b/a nếu a < 0.

    Vậy bất phương trình có tập nghiệm là

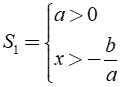
    Lý thuyết: Bất phương trình bậc nhất một ẩn

    hoặc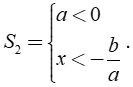Lý thuyết: Bất phương trình bậc nhất một ẩn

    Các dạng toán như ax + b < 0, ax + b ≤ 0, ax + b ≥ 0 tương tự như trên

    Ví dụ 1: Giải bất phương trình 2x - 3 > 0

    Hướng dẫn:

    Ta có: 2x - 3 > 0

    ⇔ 2x > 3 (chuyển - 3 sang VP và đổi dấu)

    ⇔ 2x:2 > 3:2 (chia cả hai vế cho 2)

    ⇔ x > 3/2.

    Vậy bất phương trình đã cho có tập nghiệm là { x| x > 3/2 }.

    Ví dụ 2: Giải bất phương trình 2x - 1 ≤ 3x - 7

    Hướng dẫn:

    Ta có: 2x - 1 ≤ 3x - 7 ⇔ - 1 + 7 ≤ 3x - 2x

    ⇔ x ≥ 6.

    Vậy bất phương trình đã cho có tập nghiệm là { x| x ≥ 6 }.

    B. Trắc nghiệm & Tự luận

    I. Bài tập trắc nghiệm

    Bài 1: Bất phương trình ax + b > 0 vô nghiệm khi

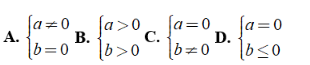
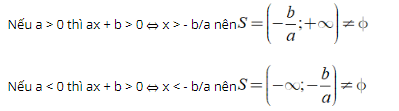
    Lý thuyết: Bất phương trình bậc nhất một ẩn

    Lý thuyết: Bất phương trình bậc nhất một ẩn

    Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0

    Với b > 0 thì S = R.

    Với b ≤ 0 thì S = Ø

    Chọn đáp án D.

    Bài 2: Tập nghiệm S của bất phương trình: 5x - 1 ≥ (2x)/5 + 3 là?

    A. S = R

    B. S = ( - ∞ ;2 )

    C. S = ( - 5/2; + ∞ )

    D. [ 20/23; + ∞ )

    Ta có: 5x - 1 ≥ (2x)/5 + 3

    ⇔ 25x - 5 ≥ 2x + 15

    ⇔ 23x ≥ 20

    ⇔ x ≥ 20/23.

    Vậy tập nghiệm của bất phương trình là [ 20/23; + ∞ )

    Chọn đáp án D.

    Bài 3: Bất phương trìnhLý thuyết: Bất phương trình bậc nhất một ẩn có bao nhiêu nghiệm nguyên lớn hơn - 10?

    A. 4 

    B. 5 

    C. 9 

    D. 10

    Ta có

    Lý thuyết: Bất phương trình bậc nhất một ẩn

    ⇔ 9x + 15 - 6 ≤ 2x + 4 + 6

    ⇔ x ≤ - 5.

    Vì x ∈ Z, - 10 < x ≤ - 5 nên có 5 nghiệm nguyên.

    Chọn đáp án B.

    Bài 4: Tập nghiệm S của bất phương trình: (1 - √ 2)x < 3 - 2√ 2 là?

    A. S = (- ∞ ;1 - √ 2)

    B. S = (1 - √ 2 ; + ∞)

    C. S = R

    D. S = Ø

    Ta có:

    (1 - √ 2)x < 3 - 2√ 2

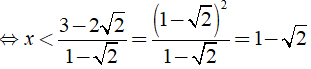
    Lý thuyết: Bất phương trình bậc nhất một ẩn

    Vậy tập nghiệm của bất phương trình là S = ( 1 - √ 2 ; + ∞ )

    Chọn đáp án B.

    Bài 5: Bất phương trình (2x - 1)(x + 3) - 3x + 1 ≤ (x - 1)(x + 3) + x2 - 5 có tập nghiệm là?

    A. S = (- ∞ ; - 2/3)

    B. S = [- 2/3; + ∞)

    C. S = R

    D. S = Ø

    Ta có:

    (2x - 1)(x + 3) - 3x + 1 ≤ (x - 1)(x + 3) + x2 - 5

    ⇔ 2x2 + 5x - 3 - 3x + 1 ≤ x2 + 2x - 3 + x2 - 5

    ⇔ 0x ≤ - 6

    ⇔ x ∈ Ø → S = Ø

    Chọn đáp án D.

    II. Bài tập tự luận

    Bài 1: Tìm tập nghiệm của các bất phương trình sau:

    a) (x + √ 3)2 ≥ (x - √ 3)2 + 2

    b) x + √ x < (2√ x + 3)(√ x - 1)

    c) (x - 3 )√ (x - 2) ≥ 2

    Hướng dẫn:

    a) Ta có: ( x + √ 3 )2 ≥ (x - √ 3)2 + 2

    ⇔ x2 + 2√ 3 x + 3 ≥ x2 - 2√ 3 x + 3 + 2

    ⇔ 4√ 3 x ≥ 2 ⇔ x ≥ √ 3 /6 → S = (√ 3 /6; + ∞)

    Vậy bất phương trình đã cho có tập nghiệm là S = (√ 3 /6; + ∞)

    b) Ta có: x + √ x < (2√ x + 3)(√ x - 1)

    Điều kiện: x ≥ 0

    ⇔ x + √ x < 2x - 2√ x + 3√ x - 3

    ⇔ - x < - 3 ⇔ x > 3

    Kết hợp điều kiện, tập nghiệm bất phương trình là: S = (3; + ∞)

    Vậy bất phương trình đã cho có tập nghiệm là S = (3; + ∞)

    c) Ta có: (x - 3)√ (x - 2) ≥ 2

    Điều kiện: x ≥ 2

    Bất phương trình tương đương là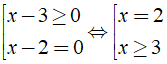Lý thuyết: Bất phương trình bậc nhất một ẩn

    Vậy tập nghiệm của bất phương trình là S = 2 ∪ [ 3; + ∞ )

    Bài 2: Có bao nhiêu giá trị thực của tham số m để bất phương trình ( m2 - m )x < m vô nghiệm là?

    Hướng dẫn:

    Rõ ràng nếu m2 - m ≠ 0 ⇔ 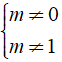Lý thuyết: Bất phương trình bậc nhất một ẩnthì bất phương trình luôn có nghiệm.

    Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.

    Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R

    Vậy với m = 0 thì bất phương trình trên vô nghiệm.

    Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:

    Chuyên đề Liên hệ giữa thứ tự và phép cộng

    Chuyên đề Liên hệ giữa thứ tự và phép nhân

    Chuyên đề Bất phương trình một ẩn

    Chuyên đề Phương trình chứa dấu giá trị tuyệt đối

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,409 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: