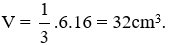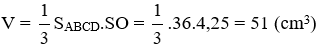Nội dung bài viết

    Xem thêm

    Chuyên đề Thể tích của hình chóp đều (2022) - Toán 8

    Với Chuyên đề Thể tích của hình chóp đều (2022) - Toán 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.

    1 684 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Chuyên đề Thể tích của hình chóp đều - Toán 8

    A. Lý thuyết

    Thể tích của hình chóp đều bằng 13 diện tích đáy nhân với chiều cao:

    V=13S.h

    ( S là diện tích đáy, h là chiều cao)

    B. Trắc nghiệm & Tự luận

    I. Bài tập trắc nghiệm

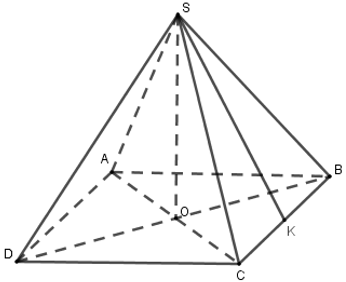
    Bài 1: Thể tích của hình chóp tứ giác đều có chiều cao 6cm, cạnh đáy 4cm là

    A. 32cm3

    B. 24cm3

    C. 144cm3

    D. 96cm3

    Lời giải

    Trắc nghiệm Hình chóp đều và hình chóp cụt đều có đáp án

    Đáy của hình chóp tứ giác đều là hình vuông nên diện tích đáy là S = 42 = 16cm2

    Thể tích cần tìm là: Trắc nghiệm Hình chóp đều và hình chóp cụt đều có đáp án

    Đáp án cần chọn là: A

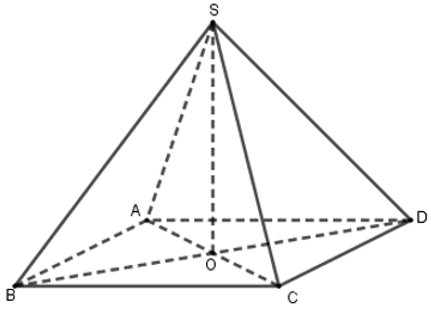
    Bài 2: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng 6cm. Thể tích hình chóp gần nhất với số nào dưới đây?

    A. 51cm3

    B. 25cm3

    C. 755cm3

    D. 65cm3  

    Lời giải

    Trắc nghiệm Hình chóp đều và hình chóp cụt đều có đáp án

    Diện tích đáy: SABCD = 62 = 36(cm2)

    Xét tam giác ABC có: AC2 = AB2 + BC2 = 62 + 62 = 72

    ⇒ AC ≈ 8,5 ⇒ AO = Trắc nghiệm Diện tích hình chữ nhật có đáp ánAC = 4,25

    Tam giác SOA vuông tại O có: SA2 = SO2 + OA2

    ⇔ 62 = SO2 + 4,252 ⇔ SO = 4,25

    Thể tích hình chóp: Trắc nghiệm Hình chóp đều và hình chóp cụt đều có đáp án

    Đáp án cần chọn là: A

    II. Bài tập tự luận

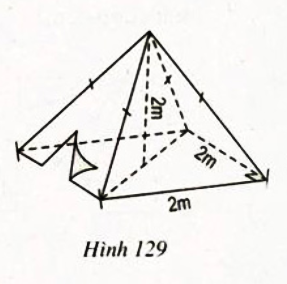
    Bài 1: Hình 129 là một cái lều ở trại hè của học sinh kèm theo các kích thước.

    a) Thể tích không khí bên trong lều là bao nhiêu?

    b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, ... biết √5 ≈ 2,24).

    Bài 44 trang 123 SGK Toán 8 tập 2

    Lời giải chi tiết

    Bài 44 trang 123 SGK Toán 8 tập 2

    a. Hình dạng của lều là hình chóp đều có đáy là hình vuông cạnh bằng 2m, chiều cao bằng 2m.

    Thể tích không khí trong lều bằng thể tích lều và bằng: V = \frac{1}{3}.2.2.2 = \frac{8}{3}\left( {c{m^3}} \right)

    b. Số vải bạt cần thiết đề dựng lều chính là diện tích xung quanh của lều.

    \begin{matrix} S{H^2} = O{S^2} + O{H^2} = O{S^2} + {\left( {\dfrac{{BC}}{2}} \right)^2} = {2^2} + {1^2} = 5 \Rightarrow SH = \sqrt 5 \left( m \right) \hfill \\ \Rightarrow {S_{xq}} = p.d = \frac{1}{2}.2.4.\sqrt 5 = 4\sqrt 5 \left( {c{m^2}} \right) \hfill \\ \end{matrix}

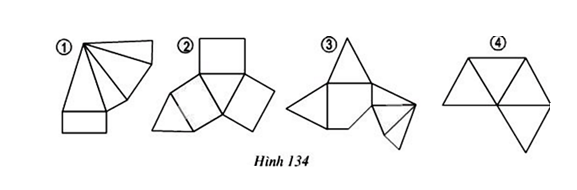
    Bài 2: Trong các miếng bìa ở hình 134, miếng nào khi gấp và dán lại thì được một hình chóp đều?

    Bài 47 Trang 124 SGK Toán 8 tập 2

    Lời giải chi tiết

    Hình 1: Khi gấp lại không được hình chóp đều vì hình chóp thu được có đáy là hình chữ nhật. Không là đa giác đều.

    Hình 2: Khi gấp lại ta được hình lăng trụ đứng đáy tam giác đều, không phải là hình chóp tam giác đều.

    Hình 3: Khi gấp lại không được hình chóp tam giác đều vì hình chóp thu được có được đáy là hình ngũ giác không phải là ngũ giác đều.

    Hình 4: Khi gấp lại không được hình chóp đều vì hình thu được là hình chóp đều thiếu một mặt đáy và dư một mặt bên.

    Bài 3: a) Tính thể tích của hình chóp đều (h.136).

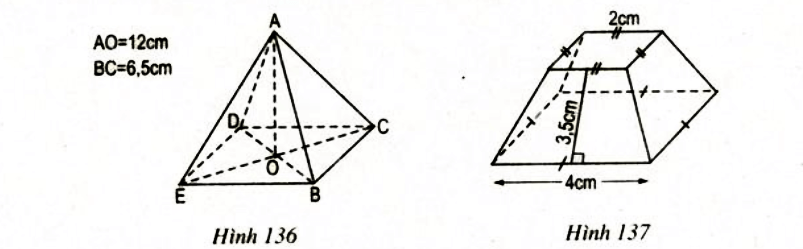
    Bài 50 Trang 125 SGK Toán 8 tập 2

    b) Tính diện tích xung quanh của hình chóp cụt đều (h.137).

    Lời giải chi tiết

    a. Thể tích hình chóp đều: V = \frac{1}{3}.12.{\left( {6,5} \right)^2} = 169\left( {c{m^3}} \right)

    b. Diện tích xung quanh của hình chóp cụt đều là: {S_{xq}} = 4.\frac{{\left( {2 + 4} \right).3,5}}{2} = 42\left( {c{m^2}} \right)

    Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:
    Chuyên đề Hình hộp chữ nhật
    Chuyên đề Thể tích của hình hộp chữ nhật
    Chuyên đề Thể tích của hình lăng trụ đứng
    Chuyên đề Hình chóp đều và hình chóp cụt đều
    Chuyên đề Diện tích xung quanh của hình chóp đều

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 684 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: