Nội dung bài viết

    Xem thêm

    Chuyên đề Tứ giác (2022) - Toán 8

    Với Chuyên đề Tứ giác (2022) - Toán 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.

    1 1,951 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Chuyên đề Tứ giác - Toán 8

    A. Lý thuyết

    1. Định nghĩa tứ giác

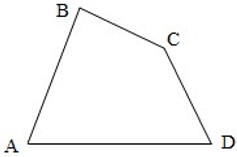
    Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

    Lý thuyết: Tứ giác

    Chú ý:

    Tứ giác ABCD còn được gọi tên là tứ giác BCDA,ADCB, ... . Các điểm A,B,C,D được gọi là các đỉnh. Các đoạn thẳng AB,BC,CD,DA được gọi là các cạnh.

    Tứ giác ABCD trên hình gọi là tứ giác lồi.

    Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

    2. Tổng các góc của một tứ giác

    Định lí: Tổng các góc của một tứ giác bằng 3600.

    Lý thuyết: Tứ giác

    Tổng quát: A^+ B^ + C^+D^ˆ = 3600.

    Ví dụ: Cho tứ giác ABCD trong đó có A^ = 600, C^= 1500, D^= 750. Tính số đo của góc B^ˆ?

    Hướng dẫn:

    Lý thuyết: Tứ giác

    Theo định lý, tổng các góc của một tứ giác bằng 3600.

    Khi đó ta có: ˆA^ + B^ +C^+ D^ = 3600.

    ⇔ 600 + B⏞ + 1500 + 750 = 3600

    ⇔ B⏞= 3600 - 2850 = 750.

    Vậy B⏞= 750.

    B. Trắc nghiệm & Tự luận

    I. Bài tập trắc nghiệm

    Bài 1: Cho tứ giác ABCD, trong đó A^ +B^ = 1400. Tổng C^+D^ = ?

    A. 2200 

    B. 2000 

    C. 1600 

    D. 1500

    Định lí: Tổng các góc của một tứ giác bằng 3600.

    Khi đó ta có A^ + B^ + C^ + D^ = 3600. ⇒ ( C^ + D^ˆ ) = 3600 - ( A^ + B^ ) = 3600 - 1400 = 2200

    Chọn đáp án A.

    Bài 2: Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là?

    A. 1200; 900 ;600 ;300.

    B. 1400 ;1050 ;700 ;350.

    C. 1440 ;1080 ;720 ;360.

    D. Cả A, B, C đều sai.

    Định lí: Tổng các góc của một tứ giác bằng 3600.

    Theo giải thiết ta có A:B:C:D = 4:3:2:1 ⇒ A^ = 4D^; B^ = 3D^; C^= 2D^

    Khi đó ta có A^+B^+C^+D^ˆ = 3600 ⇔ 4D^+3D^+2D^+D^ =3600

    ⇔ 10D^ = 3600 ⇔ D^ˆ = 360.

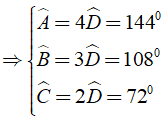
    Bài tập: Tứ giác

    Chọn đáp án C.

    Bài 3: Chọn câu đúng trong các câu sau:

    A. Tứ giác ABCD có 4 góc đều nhọn.

    B. Tứ giác ABCD có 4 góc đều tù.

    C. Tứ giác ABCD có 2 góc vuông và 2 góc tù.

    D. Tứ giác ABCD có 4 góc đều vuông.

    Theo định lí: Tổng các góc của một tứ giác bằng 3600.

    Nhận xét:

    + α là góc nhọn thì 0 < α < 900 ⇒ 0 < 4.α < 3600.

    ⇒ Không tồn tại tứ giác ABCD có 4 góc đều nhọn. ⇒ Loại A.

    + α là góc tù thì 900 < α < 1800 ⇒ 3600 < 4.α < 7200

    ⇒ Không tồn tại tứ giác ABCD có 4 góc đều tù. ⇒ Loại B.

    + α là góc vuông thì α = 900; β là góc tù thì 900 < β < 1800 ⇒ 1800 < 2.β < 3600

    Khi đó ta có : 1800 + 1800 < 2α + 2β < 1800 + 3600⇒ 3600 < 2α + 2β < 5400

    ⇒ Không tồn tại tứ giác ABCD có 2 góc nhọn và 2 góc tù. ⇒ Loại C.

    + Vì tứ giác có 4 góc vuông thì tổng các góc bằng 3600.Chọn đáp án D.

    Bài 4: Cho tứ giác ABCD có Aˆ = 650;Bˆ = 1170;Cˆ = 710. Số đo góc Dˆ = ?

    A. 1190. 

    B. 1070. 

    C. 630. 

    D. 1260.

    Định lí: Tổng các góc của một tứ giác bằng 3600.

    Khi đó ta có Aˆ + Bˆ + Cˆ + Dˆ = 3600

    ⇒ Dˆ = 3600 - (Aˆ + Bˆ + Cˆ) = 3600 - (650 + 1170 + 710)

    ⇒ Dˆ = 3600 - 2530 = 1070.

    Chọn đáp án B.

    Bài 5: Cho tứ giác ABCD trong đó có B^= 750;D^ˆ = 1200. Khi đó A^+C^ˆ = ?

    A. 1900 

    B. 1300 

    C. 2150 

    D. 1650

    Định lí: Tổng các góc của một tứ giác bằng 3600.

    Khi đó ta có A^+B^+C^+D^= 3600 ⇒ ( C^+A^ˆ ) = 3600 - (B^+D^ˆ ) = 3600 - 1950 = 1650

    Chọn đáp án D.

    II. Bài tập tự luận

    Bài 1: Cho tứ giác ABCD trong đó Aˆ = 730,Bˆ = 1120,Dˆ = 840. Tính số đo góc Cˆ?

    Hướng dẫn:

    Áp dụng định lí: Tổng các góc của một tứ giác bằng 3600.

    Khi đó ta có A^+B^+C^+D^ˆ = 3600 ⇒ C^ˆ = 3600 - ( A^+B^+D^ˆ ) = 3600 - ( 730 + 1120 + 840 )

    ⇒ C^ = 3600 - 2690 = 910.

    Vậy số đo của góc C^ cần tìm là C^ = 910.

    Bài 2: Cho tứ giác ABCD có A^ = 700,B^ = 900. Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc CODˆ ?

    Hướng dẫn:

    Áp dụng định lí: Tổng các góc của một tứ giác bằng 3600.

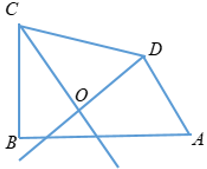
    Bài tập: Tứ giác

    Ta có Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇒ Cˆ + Dˆ = 3600 - (Aˆ + Bˆ) = 3600 - (700 + 900)

    ⇒ Cˆ + Dˆ = 2000

    Theo giả thiết, ta có OC, OD là các đường phân giác

    Khi đó ta có 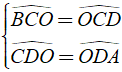Bài tập: Tứ giác

    ⇒ C^ + D^ˆ = BCO^ˆ + OCD^ˆ + CDO^ˆ + ODA^ˆ = 2OCD^ˆ + 2ODC^ˆ

    ⇔ 2(OCD^ˆ + ODC^ˆ) = 2000 ⇔ OCD^ˆ + ODC^ˆ = 1000

    Xét Δ OCD có ODC^ ˆ + ODC^ˆ + COD^ˆ = 1800 

    ⇒COD^ = 1800 - (OCD^ˆ + ODC^ˆ) = 1800 - 1000 = 800.

    Vậy COD^ˆ = 800.

    Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:

    Chuyên đề Hình thang

    Chuyên đề Hình thang cân

    Chuyên đề Đường trung bình của tam giác, của hình thang

    Chuyên đề Đối xứng trục

    Chuyên đề Hình bình hành

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,951 18/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: