Chuyên đề Hình bình hành (2022) - Toán 8
Với Chuyên đề Hình bình hành (2022) - Toán 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Hình bình hành - Toán 8
A. Lý thuyết Hình bình hành
1. Định nghĩa hình bình hành
- Hình bình hành là tứ giác có các cạnh đối song song
- Tứ giác ABCD là hình bình hành ⇔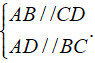

Chú ý đặc biệt: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)
2. Tính chất hình bình hành
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết hình bình hành
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ^ABEˆABE = ^CDFˆCDF .
Hướng dẫn:
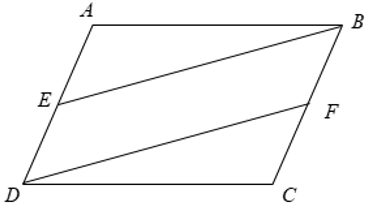
Xét tứ giác BEDF có 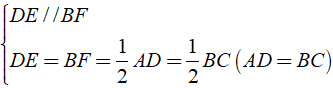
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên ^BADˆBAD = ^BCDˆBCDˆ (1)
BEDF là hình bình hành nên ^BEDˆBEDˆ = ^DFBˆDFBˆ (2)
Mà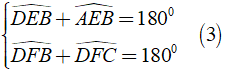
Từ ( 2 ) và ( 3 ) ⇒ ^AEBˆAEB = ^DFCˆDFCˆ (4)
Xét Δ ABE có^BAEˆBAEˆ + ^AEBˆAEBˆ + ^ABEˆABEˆ = 1800 (5)
Xét Δ DFC có ^DFCˆDFCˆ + ^FCDˆFCDˆ + ^FDCˆFDCˆ = 1800 (5)
Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ^ABEˆABE= ^CDFˆCDF (đpcm)
B. Các dạng Toán thường gặp
Dạng 1: Vận dụng tính chất hình bình hành để chứng minh tính chất hình học và tính toán
Phương pháp: Sử dụng tính chất hình bình hành
Trong hình bình hành:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Dạng 2: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình bình hành
Phương pháp: Dấu hiệu nhận biết:
+ Tứ giác có đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
C. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Chọn phương án sai trong các phương án sau?
A. Tứ giác có các cạnh đối song song là hình bình hành.
B. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
C. Tứ giác có hai góc đối bằng nhau là hình bình hành.
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Dấu hiệu nhận biết hình bình hành.
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.→ Đáp án C sai.
Chọn đáp án C.
Bài 2: Chọn phương án đúng trong các phương án sau.
A. Hình bình hành là tứ giác có hai cạnh đối song song.
B. Hình bình hành là tứ giác có các góc bằng nhau.
C. Hình bình hành là tứ giác có các cạnh đối song song.
D. Hình bình hành là hình thang có hai cạnh kề bằng nhau.
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.→ Đáp án C đúng.
Chọn đáp án C.
Bài 3: Cho hình bình hành ABCD có ˆAˆA = 1200, các góc còn lại của hình bình hành là?
A. ˆBˆBˆ = 600, ˆCˆCˆ = 1200, ˆDˆDˆ = 600.
B.ˆBˆBˆ = 1100 ; ˆCˆC= 800,ˆDˆDˆ = 600.
C. ˆBˆBˆ = 800, ˆCˆCˆ = 1200, ˆDˆDˆ = 800.
D. ˆBˆBˆ = 1200, ˆCˆC = 600, ˆDˆDˆ = 1200.
 Trong tính chất của hình bình hành:Định lí: Trong hình bình hành:
Trong tính chất của hình bình hành:Định lí: Trong hình bình hành: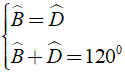
Bài 4: Cho hình bình hành ABCD có Aˆ - Bˆ = 200. Xác định số đo góc A và B?
A. Aˆ = 800, Bˆ = 1000
B. Aˆ = 1000, Bˆ = 800
C. Aˆ = 800, Bˆ = 600
D. Aˆ = 1200, Bˆ = 1000
Theo giả thiết, ta có: Aˆ - Bˆ = 200 ⇒ Aˆ = Bˆ + 200
Mặt khác ABCD là hình bình hành nên Aˆ + Bˆ = 1800
Khi đó:
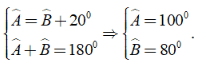
Bài 5: Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
A. AC = BD
B. ΔABD cân tại A.
C. BI là đường trung tuyến của Δ ABC
D. ˆAˆAˆ + ˆCˆCˆ =ˆB+ˆDˆB+ˆD.
Trong hình bình hành các góc đối bằng nhau
Hay 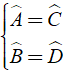 ⇒ Aˆ + Bˆ = Cˆ + Dˆ → đáp án D sai.
⇒ Aˆ + Bˆ = Cˆ + Dˆ → đáp án D sai.
+ ΔABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này→ Đáp án B sai.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.→ Đáp án A sai vì theo giả thiết chưa đủ dữ kiện
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A, C xuống BD.
a) Chứng minh AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.
Hướng dẫn:
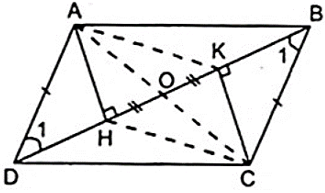
a) Từ giả thiết ta có: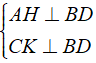 ⇒ AH // CK (1)
⇒ AH // CK (1)
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
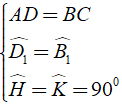
⇒ ΔADH = ΔCBK (trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tương ứng bằng nhau) (2)
Từ (1) và (2) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
b) Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường
Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
Bài 2: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:
a) AK // CI
b) DM = MN = NB
Hướng dẫn:
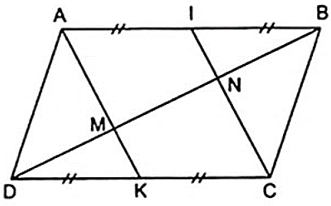
a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
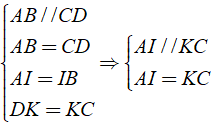
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
b) Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: ![]()
Mặt khác, ta lại có: AI = IB, CK = KD theo giả thiết:
Áp dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
![]()
⇒ DM = MN = NB
Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
