Chuyên đề Rút gọn phân thức (2022) - Toán 8
Với Chuyên đề Rút gọn phân thức (2022) - Toán 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Rút gọn phân thức - Toán 8
A. Lý thuyết
1. Quy tắc rút gọn một phân thức
Một rút gọn một phân thức đại số ta cần phải:
+ Đặt điều kiện xác định cho mẫu thức.
+ Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung
+ Chia cả tử và mẫu cho nhân tử chung giống nhau
Chú ý:
+ Có khi cần đổi dấu tử hoặc mẫu thức để xuất hiện nhân tử chung.
+ Cần chú ý tính chất A = - ( - A ).
2. Ví dụ minh họa
Ví dụ 1: Rút gọn phân thức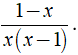
.
Hướng dẫn:
Điều kiện xác định x ≠ 0; x ≠ 1.
Ta có: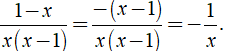 
Ví dụ 2: Rút gọn phân thức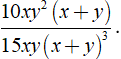
Hướng dẫn:
Điều kiện xác định xy ≠ 0; x + y ≠ 0.
Ta có:
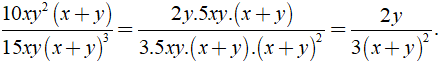
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Kết quả của rút gọn biểu thức (6x2y2)/(8xy5) là?
A. 6/8
B. (3x)/(4y3)
C. 2xy2
D. (x2y2)/(xy5)
Điều kiện xác định là x ≠ 0;y ≠ 0.
Ta có (6x2y2)/(8xy5) = (2.3.xy2.x)/(2.4.xy2.y3) = (3x)/(4y3).
Chọn đáp án B.
Bài 2: Kết quả của rút gọn biểu thức (x2 - 16)/(4x - x2) (x ≠ 0, x ≠ 4) là?
A. (x - 4)/x.
B. (x + 4)/(x - 4).
C. (x + 4)/( - x)
D. (4 - x)/( - x).
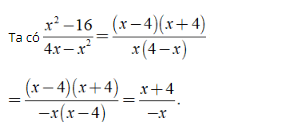
Bài 3: Rút gọn biểu thức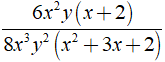
là
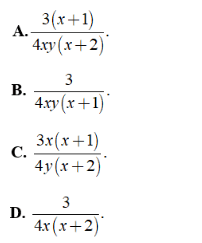
Điều kiện xác định x,y ≠ 0; x2 + 3x + 2 ≠ 0
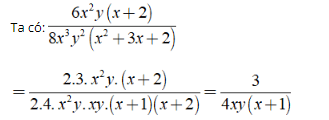
Bài 4: Rút gọn phân thức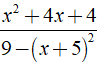
được kết quả là?
A. (- x - 2)/(x + 8)
B. (x + 2)/(x - 8)
C. (x + 2)/(x + 8)
D. (- x - 2)/(x - 8)
Điều kiện xác định: 9 - ( x + 5 )2 ≠ 0
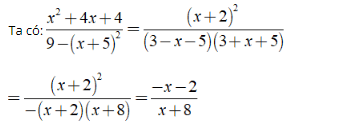
Chọn đáp án A.
Bài 5: Cho kết quả sai trong các phương án sau đây?
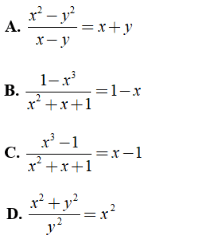
II. Bài tập tự luận
Bài 1: Rút gọn các biểu thức sau
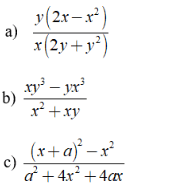
Hướng dẫn:
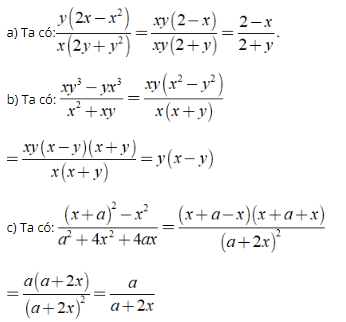
Bài 2: Rút gọn phân thức sau:
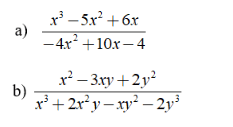
Hướng dẫn:
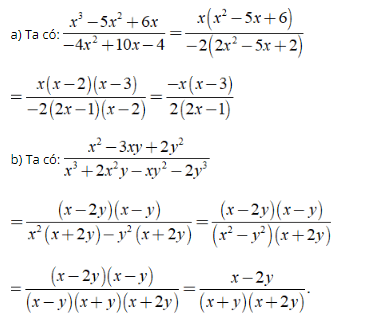
Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:
Chuyên đề Tính chất cơ bản của phân thức
Chuyên đề Quy đồng mẫu thức nhiều phân thức
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8