Chuyên đề Phương trình chứa ẩn ở mẫu (2022) - Toán 8
Với Chuyên đề Phương trình chứa ẩn ở mẫu (2022) - Toán 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Phương trình chứa ẩn ở mẫu - Toán 8
A. Lý thuyết
1. Tìm điều kiện xác định của một phương trình
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0.
Điều kiện xác định của phương trình viết tắt là ĐKXĐ.
Ví dụ: Tìm điều kiện xác định của các phương trình sau
a) (x - 1)/(x + 2) + 1 = 1/(x - 2).
b) (x - 1)/(1 - 2x) = 1.
Hướng dẫn:
a) Ta thấy x + 2 ≠ 0 khi x ≠ - 2 và x - 2 ≠ 0 khi x ≠ 2.
Do đó ĐKXĐ của phương trình (x - 1)/(x + 2) + 1 = 1/(x - 2) là x ≠ ± 2.
b) Ta thấy 1 - 2x ≠ 0 khi x ≠ 1/2.
Do đó ĐKXĐ của phương trình (x - 1)/(1 - 2x) = 1 là x ≠ 1/2.
2. Giải phương trình chứa ẩn ở mẫu
Ta thường qua các bước:
Bước 1: Tìm điều kiện xác của phương trình
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu.
Bước 3: Giải phương trình tìm được.
Bước 4: Kết luận.
Nghiệm của phương trình là giá trị của ẩn thoả mãn ĐKXĐ của phương trình.
Ví dụ 1: Giải phương trình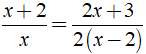
Hướng dẫn:
Bước 1: Điều kiện xác định: x ≠ 0; x ≠ 2.
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu
Ta có: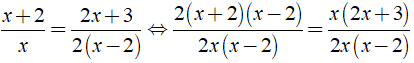
⇒ 2(x - 2)(x + 2) = x(2x + 3)
Bước 3: Giải phương trình
Ta có: 2(x - 2)(x + 2) = x(2x + 3) ⇔ 2(x2 - 4) = 2x2 + 3x
⇔ 2x2 - 8 = 2x2 + 3x ⇔ 3x = - 8 ⇔ x = - 8/3.
Bước 4: Kết luận
So sánh với ĐKXĐ, ta thấy x = - 8/3 thỏa mãn.
Vậy phương trình đã cho có tập nghiệm S = { - 8/3 }.
Ví dụ 2: Giải phương trình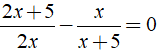
Hướng dẫn:
+ ĐKXĐ: x ≠ 0; x ≠ - 5.
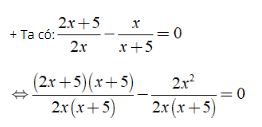
⇒ (2x + 5)(x + 5) - 2x2 = 0
⇔ 2x2 + 10x + 5x + 25 - 2x2 = 0 ⇔ 15x = - 25 ⇔ x = - 5/3.
+ So sánh với ĐKXĐ ta thấy x = - 5/3 thỏa mãn điều kiện.
Vậy phương trình đã cho có tập nghiệm là S = {- 5/3}.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Nghiệm của phương trình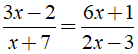 là?
là?
A. x = - 1.
B. x = - 1/56.
C. x = 1.
D. x = 1/56.
+ ĐKXĐ: x ≠ - 7;x ≠ 3/2.
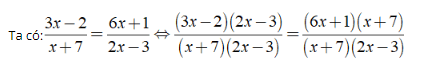
⇔ (3x - 2)(2x - 3) = (6x + 1)(x + 7)
⇔ 6x2 - 13x + 6 = 6x2 + 43x + 7
⇔ 56x = - 1
⇔ x = - 1/56.
Vậy phương trình đã cho có nghiệm x = - 156.
Chọn đáp án B.
Bài 2: Nghiệm của phương trình (x + 1)/(3 - x) = 2 là?
A. x = - 5/3.
B. x = 0.
C. x = 5/3.
D. x = 3.
+ ĐKXĐ: x ≠ 3.
+ Ta có: (x + 1)/(3 - x) = 2
⇔ x + 1 = 2( 3 - x )
⇔ x + 1 = 6 - 2x
⇔ 3x = 5
⇔ x = 5/3.
Vậy phương trình có nghiệm là x = 5/3.
Chọn đáp án C.
Bài 3: Tập nghiệm của phương trình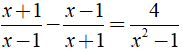 là?
là?
A. S = {± 1}.
B. S = {0;1}.
C. S = {1}.
D. S = {Ø}.
+ ĐKXĐ: x2 - 1 ≠ 0 ⇒ x ≠ ± 1.
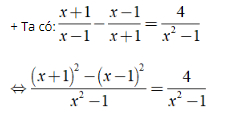
⇔ (x + 1)2 - (x - 1)2 = 4
⇔ x2 + 2x + 1 - x2 + 2x - 1 = 4
⇔ 4x = 4
⇔ x = 1.
So sánh điều kiện, ta thấy x = 1 không thỏa mãn.
Vậy phương trình đã cho có tập nghiệm là S = { Ø }.
Chọn đáp án D.
Bài 4: Nghiệm của phương trình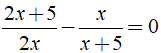 là?
là?
A. x = 5/3.
B. x = - 5/3.
C. x = - 2.
D. x = 2.
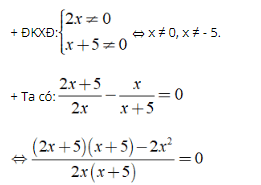
⇔ (2x2 + 15x + 25) - 2x2 = 0
⇔ 15x + 25 = 0
⇔ x = - 5/3.
Vậy phương trình đã cho có nghiệm là x = - 5/3.
Chọn đáp án B.
Bài 5: Giá trị của m để phương trình (x - m)/(x + 2) = 2 có nghiệm x = - 3 là?
A. m = 0.
B. m = 1.
C. m = - 1.
D. m = 2.
+ Điều kiện: x ≠ - 2.
+ Phương trình có nghiệm x = - 3, khi đó ta có: (- 3 - m)/(- 3 + 2) = 2
⇔ (- m - 3)/(- 1) = 2
⇔ m + 3 = 2
⇔ m = - 1.
Vậy m = - 1 là giá trị cần tìm.
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Giải các phương trình sau:
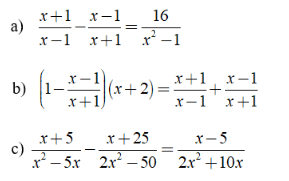
Hướng dẫn:
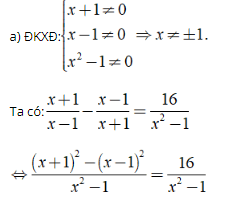
⇔ (x + 1)2 - (x - 1)2 = 16
⇔ (x2 + 2x + 1) - (x2 - 2x + 1) = 16
⇔ 4x = 16 ⇔ x = 4.
Vây phương trình đã cho có nghiệm x = 4.
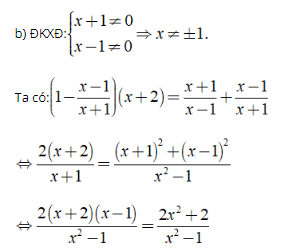
⇔ 2(x2 + x - 2) = 2x2 + 2
⇔ 2x = 6 ⇔ x = 3.
Vậy phương trình đã cho có nghiệm là x = 3.
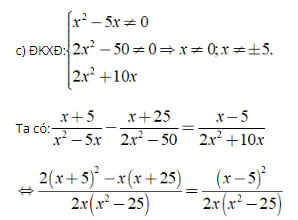
⇔ 2(x2 + 10x + 25) - (x2 + 25x) = x2 - 10x + 25
⇔ x2 - 5x + 50 = x2 - 10x + 25
⇔ 5x = - 25 ⇔ x = - 5.
Vậy phương trình đã cho có nghiệm x = - 5.
Bài 2: Giải các phương trình sau:
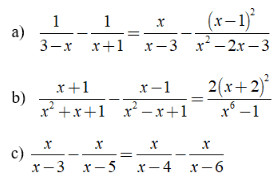
Hướng dẫn:
a) ĐKXĐ: x ≠ - 1;x ≠ 3.
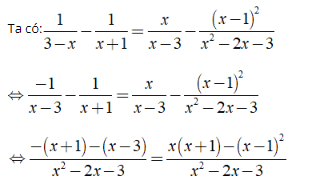
⇔ - x - 1 - x + 3 = x2 + x - x2 + 2x - 1
⇔ 5x = 3 ⇔ x = 3/5.
Vậy phương trình đã cho có nghiệm là x = 3/5.
b) ĐKXĐ: x ≠ 3, x ≠ 4, x ≠ 5, x ≠ 6.
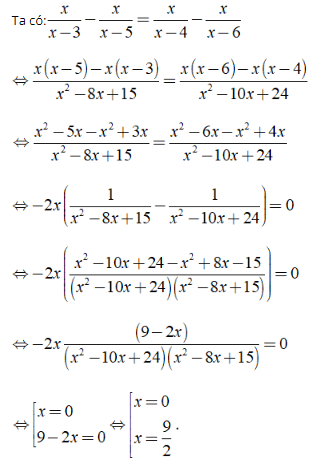
Vậy phương trình đã cho có nghiệm là x = 0;x = 9/2.
c) ĐKXĐ: x ≠ 1.
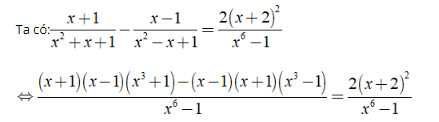
⇔ (x2 - 1 )( x3 + 1) - (x2 - 1)(x3 - 1) = 2(x2 + 4x + 4)
⇔ (x5 + x2 - x3 - 1) - (x5 - x2 - x3 + 1) = 2(x2 + 4x + 4)
⇔ 2x2 - 2 = 2x2 + 8x + 8
⇔ 8x = - 10 ⇔ x = - 5/4.
Vậy phương trình đã cho có nghiệm là x = - 5/4.
Xem thêm các bài Chuyên đề Toán lớp 8 hay, chi tiết khác:
Chuyên đề Mở đầu về phương trình
Chuyên đề Phương trình bậc nhất một ẩn và cách giải
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
