Số trung bình cộng. Số trung vị. Mốt và cách giải bài tập (2024) chi tiết nhất

Số trung bình cộng. Số trung vị. Mốt và cách giải bài tập – Toán lớp 10

A. Lí thuyết.

1. Số trung bình cộng:

Ta có thể tính số trung bình cộng của các số liệu thống kê theo các công thức:

+ Với bảng phân bố tần số và tần suất: $n_i$, $f_i$ lần lượt là tần số, tần suất của giá trị $x_i$, n là số các số liệu thống kê. Ta có số trung bình cộng:

$\overline{x}=\frac{1}{n}(n_1{x}_1+n_2{x}_2+\mathrm{...}+n_k{x}_k)=f_1{x}_1+f_2{x}_2+\mathrm{...}+f_k{x}_k$

+ Với bảng phân bố tần số và tần suất ghép lớp: $c_i$, $n_i$, $f_i$ lần lượt là giá trị đại diện, tần số, tần suất của lớp thứ i, n là số các số liệu thống kê. Ta có số trung bình cộng:

$\overline{x}=\frac{1}{n}(n_1{c}_1+n_2{c}_2+\mathrm{...}+n_k{c}_k)=f_1{c}_1+f_2{c}_2+\mathrm{...}+f_k{c}_k$

2. Số trung vị:

Khi ta sắp thứ tự các số liệu thống kê thành dãy không giảm (hoặc không tăng). Số trung vị (của các số liệu thống kê đã cho), kí hiệu là $M_e$, là số đứng giữa dãy nếu số phần tử là lẻ và là trung bình cộng của hai số đứng giữa dãy nếu số phần tử là chẵn.

3. Mốt: Mốt của một bảng phân bố tần số là giá trị có tần số lớn nhất và được kí hiệu là $M_0$.

B. Các dạng toán và phương pháp giải

Dạng 1. Tính số trung bình cộng:

Phương pháp giải:

+ Với bảng phân bố tần số, tần suất:

Số trung bình cộng:

$\overline{x}=\frac{1}{n}(n_1{x}_1+n_2{x}_2+\mathrm{...}+n_k{x}_k)=f_1{x}_1+f_2{x}_2+\mathrm{...}+f_k{x}_k$

+ Với bảng phân bố tần số, tần suất ghép lớp:

Số trung bình cộng:

$\overline{x}=\frac{1}{n}(n_1{c}_1+n_2{c}_2+\mathrm{...}+n_k{c}_k)=f_1{c}_1+f_2{c}_2+\mathrm{...}+f_k{c}_k$

Ví dụ: Trong một trường THPT, để tìm hiểu tình hình học môn Toán của lớp 10A, người ta cho hai lớp thi Toán theo cùng một đề và lập được bảng phân bố tần số:

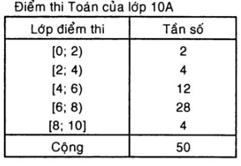
Hãy tính số trung bình cộng của bảng phân bố.

Lời giải:

Trung bình cộng các điểm thi Toán của lớp 10A là:

$\overline{x}=\frac{1}{50}.\left(\frac{0+2}{2}.2+\frac{2+4}{2}.4+\frac{4+6}{2}.12+\frac{6+8}{2}.28+\frac{8+10}{2}.4\right)=6,12$

Vậy trung bình cộng của điểm thi Toán lớp 10A là 6,12.

Dạng 2: Tìm số trung vị:

Phương pháp giải:

+ Sắp xếp thứ tự các số liệu thống kê theo thứ tự không giảm.

+ Nếu có n số liệu, n = 2k + 1 thì $M_e=x_{k+1}$

+ Nếu có n số liệu, n = 2k thì $M_e=\frac{x_k+x_{k+1}}{2}$

Ví dụ: Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch là: 650; 840; 690; 2500; 720; 670; 3000. (đơn vị: nghìn đồng). Tìm số trung vị của các số liệu thống kê đã cho. Nêu ý nghĩa của kết quả đã tìm được.

Lời giải:

Sắp xếp thứ tự các số liệu thống kê, ta thu được dãy tăng các số liệu sau: 650; 670; 690; 720; 840; 2500; 3000 (nghìn đồng)

Ta có số các số liệu thống kê là n = 7 = 2.3 + 1$\Rightarrow k=3$

$\Rightarrow$Số trung vị là $M_e=x_4=720$

Số các số liệu thống kê quá ít (n = 7 < 10), do đó không nên chọn số trung bình cộng làm đại diện cho các số liệu đã cho. Trong trường hợp này ta chọn số trung vị làm đại diện cho tiền lương hàng tháng của mỗi người trong 7 nhân viên được khảo sát.

Dạng 3. Tìm Mốt:

Phương pháp giải:

Trong bảng phân bố tần số, giá trị có tần số lớn nhất được gọi là mốt của bảng phân bố kí hiệu $M_0$.

Ví dụ: Điều tra tiền lương hàng tháng của 30 công nhân của một xưởng may, ta có bảng phân bố tần số như sau:

Hãy tính số trung bình cộng, mốt của bảng phân bố trên.

Lời giải:

Số trung bình cộng tiền lương hàng tháng của công nhân là:

$\overline{x}=\frac{1}{30}.\left(300.3+500.5+700.6+800.5+900.6+1000.5\right)\approx 733,3$ (nghìn đồng)

Bảng phân bố đã cho có hai giá trị có tần số bằng nhau và lớn hơn tần số của những giá trị khác là 700 và 900. Trong trường hợp này ta xem rằng có hai mốt là ${M_0}^{\left(1\right)}=700$ và ${M_0}^{\left(2\right)}=900$

C. Bài tập tự luyện.

Bài 1: Cho biết tình hình thu hoạch lúa vụ mùa năm 1980 của ba hợp tác xã ở địa phương V như sau:

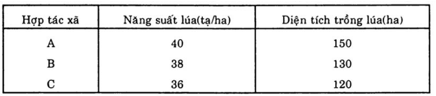
Hãy tính năng suất lúa trung bình của vụ mùa năm 1980 trong ba hợp tác xã trên.

Đáp án: 38,15 tạ/ha

Bài 2: Có 100 học sinh tham dự kì thi học sinh giỏi toán (thang điểm 20). Kết quả được cho trong bảng sau đây:

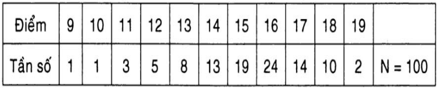
Hãy tính số trung bình và mốt của bảng số liệu trên.

Đáp án: $\overline{x}=15,23$,$M_0=16$

Bài 3: Một nhà thực vật học đo chiều dài của 74 chiếc lá cây và thu được số liệu sau (đơn vị mm).

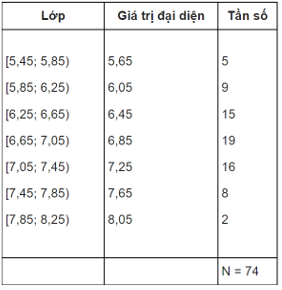
Hãy tính chiều dài trung bình của 74 chiếc lá.

Đáp án: 6,8 (mm)

Bài 4: Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp đến cao như sau: 0; 0; 63; 65; 69; 70; 72; 78; 81; 85; 89. Tính điểm trung bình, mốt, số trung vị của số liệu.

Đáp án: $\overline{x}\approx 61,09$, $M_0=0$,$M_e=70$

Bài 5: Điểm thi toán của 9 học sinh như sau: 1; 6; 7; 3; 1; 8; 9; 8; 10. Tìm số trung vị của số liệu.

Đáp án: 7

Bài 6: Điểm thi lại của 4 học sinh môn Ma trận như sau: 1; 2,5; 8; 9,5. Tìm số trung vị của số liệu.

Đáp án: 5,25

Bài 7: Một cửa hàng bán 6 loại quạt với giá tiền là 100, 150, 300, 350, 400, 500 (nghìn đồng). Số quạt cửa hàng bán ra trong mùa hè vừa qua được thống kê trong bảng tần số sau:

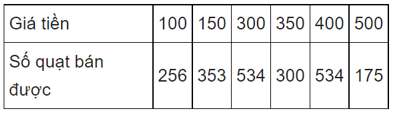
Tìm mốt của số liệu.

Đáp án: ${M_0}^{\left(1\right)}=300$ và ${M_0}^{\left(2\right)}=400$

Bài 8: Tìm mốt của bảng số liệu sau:

Đáp án: $M_0=4,8$

Xem thêm các dạng bài tập Toán lớp 10 có đáp án và lời giải chi tiết khác:

Bảng phân bố tần số và tần suất và cách giải bài tập

Biểu đồ lớp 10 và cách giải bài tập

Phương sai và độ lệch chuẩn và cách giải bài tập

Góc và cung lượng giác và cách giải bài tập

Giá trị lượng giác của cung và cách giải bài tập