Hệ trục tọa độ trong mặt phẳng và cách giải bài tập – Toán lớp 10

Hệ trục tọa độ trong mặt phẳng và cách giải bài tập – Toán lớp 10

A. Lí thuyết tổng hợp.

- Trục tọa độ (gọi tắt là trục) :

+ Định nghĩa: Trục tọa độ là một đường thẳng mà trên đó đã xác định một điểm O gọi là điểm gốc và một vectơ đơn vị $\overrightarrow{e}$.

+ Kí hiệu: $\left(O;\overrightarrow{e}\right)$

+ Tọa độ của điểm đối với trục: Cho M là một điểm tùy ý trên trục $\left(O;\overrightarrow{e}\right)$. Khi đó, tồn tại duy nhất một số k sao cho $\overrightarrow{OM}=k\overrightarrow{e}$, ta gọi số k đó là tọa độ của điểm M đối với trục $\left(O;\overrightarrow{e}\right)$.

+ Độ dài đại số trên trục: Cho hai điểm A và B trên trục $\left(O;\overrightarrow{e}\right)$ có tọa độ lần lượt là a và b. Khi đó, tồn tại duy nhất số h sao cho $\overrightarrow{AB}=h\overrightarrow{e}$, ta gọi số h đó là độ dài đại số của vectơ $\overrightarrow{AB}$ trên trục $\left(O;\overrightarrow{e}\right)$. Kí hiệu: $h=\overline{AB}$ với $\overline{AB}=b-a$. Nếu $\overrightarrow{AB}$ cùng hướng với $\overrightarrow{e}$ thì $\overline{AB}=AB$, nếu $\overrightarrow{AB}$ ngược hướng với $\overrightarrow{e}$ thì $\overline{AB}=-AB$.

+ Tính chất:

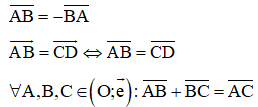
- Hệ trục tọa độ:

+ Định nghĩa: Hệ trục tọa độ $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$ gồm hai trục $\left(O;\overrightarrow{i}\right)$ và $\left(O;\overrightarrow{j}\right)$ vuông góc với nhau tại O. Điểm O gọi là gốc tọa độ. Trục $\left(O;\overrightarrow{i}\right)$ được gọi là trục hoành, kí hiệu là Ox. Trục $\left(O;\overrightarrow{j}\right)$ được gọi là trục tung, kí hiệu là Oy. Các vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$ là các vectơ đơn vị và $\left|\overrightarrow{i}\right|=\left|\overrightarrow{j}\right|=1$. Hệ trục tọa độ $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$ còn được kí hiệu là Oxy.

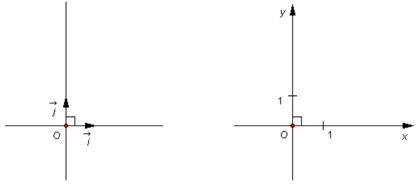
+ Mặt phẳng Oxy: Mặt phẳng mà trên đó đã cho một hệ trục Oxy được gọi là mặt phẳng tọa độ Oxy hay gọi tắt là mặt phẳng Oxy.

+ Tọa độ của vectơ: Trong mặt phẳng Oxy, cho vectơ $\overrightarrow{u}$ tùy ý. Khi đó, tồn tại cặp số (x; y) duy nhất sao cho $\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$, cặp số đó được gọi là tọa độ của vectơ $\overrightarrow{u}$ và kí hiệu là $\overrightarrow{u}$= (x; y) hoặc $\overrightarrow{u}$(x; y), trong đó, x được gọi là hoành độ và y được gọi là tung độ của vectơ $\overrightarrow{u}$.

+ Tọa độ của một điểm: Trong mặt phẳng Oxy, cho điểm M tùy ý. Tọa độ của vectơ $\overrightarrow{OM}$ đối với hệ trục Oxy chính là tọa độ của điểm M đối với hệ trục đó. Tức là $\overrightarrow{OM}=x\overrightarrow{i}+\text{y}\overrightarrow{\text{j}}\iff \overrightarrow{OM}=(x;y)\iff M(x;y)$ hoặc M = (x; y), trong đó, x được gọi là hoành độ và y được gọi là tung độ của điểm M.

+ Tọa độ của của trung điểm đoạn thẳng: Trong mặt phẳng Oxy cho các điểm $A(x_A;y_A)$, $B(x_B;y_B)$ và điểm $M(x_M;y_M)$ là trung điểm của đoạn thẳng AB thì ta có: $x_G=\frac{x_A+x_B+x_C}{3};y_G=\frac{y_A+y_B+y_C}{3}$.

+ Tọa độ của của trọng tâm tam giác: Trong mặt phẳng Oxy cho ba điểm không thẳng hàng $A(x_A;y_A)$,$B(x_B;y_B)$ , $C(x_C;y_C)$ và điểm $G(x_G;y_G)$ là trọng tâm của tam giác ABC thì ta có: $x_G=\frac{x_A+x_B+x_C}{3};y_G=\frac{y_A+y_B+y_C}{3}$.

+ Tọa độ của các vectơ $\overrightarrow{u}+\overrightarrow{v},\overrightarrow{u}-\overrightarrow{v},k\overrightarrow{u}$: Trong mặt phẳng Oxy, cho hai vectơ $\overrightarrow{u}=(x_1;y_1)$ và $\overrightarrow{v}=(x_2;y_2)$, khi đó ta có:

$$\begin{gathered} \overrightarrow{u}+\overrightarrow{v}=(x_1+x_2;y_1+y_2) \\ \overrightarrow{u}-\overrightarrow{v}=(x_1-x_2;y_1-y_2) \end{gathered}$$

$k\overrightarrow{u}=(k{x}_1;k{y}_1)$ với $k\in ℝ$

+ Tính chất:

• $\overrightarrow{u}(x;y)=\overrightarrow{v}(x\text{'};y\text{'})\iff \left\{\begin{array}{l}x=x\text{'}\\ y=y\text{'}\end{array}\right.$

• Cho điểm M (x; y) tùy ý trong mặt phẳng Oxy, nếu $M{M}_1\perp \text{O}x,M{M}_2\perp \text{Oy}$ thì $O{M}_1=x,O{M}_2=y$.

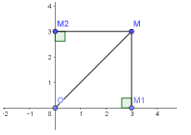
• Trong mặt phẳng Oxy, cho hai điểm $A(x_A;y_A)$ và $B(x_B;y_B)$, khi đó $\overrightarrow{AB}=(x_B-x_A;y_B-y_A)$

• Trong mặt phẳng Oxy, vectơ $\overrightarrow{u}=(x_1;y_1)$ cùng phương với vectơ $\overrightarrow{v}=(x_2;y_2)$ với  $\overrightarrow{v}\ne \overrightarrow{0}$ khi và chỉ khi tồn tại một số k sao cho:

$$\begin{gathered} \overrightarrow{u}=k\overrightarrow{v}\iff \left\{\begin{array}{l}{x}_1=k{x}_2\\ y_1=k{y}_2\end{array}\right. \\ \iff \frac{x_1}{x_2}=\frac{y_1}{y_2}=k\iff x_1{y}_2=x_2{y}_1 \end{gathered}$$

B. Các dạng bài.

Dạng 1: Xác định tọa độ một điểm.

Phương pháp giải:

- Áp dụng các kiến thức về tọa độ của điểm trên trục và trong mặt phẳng:

+)$\overrightarrow{OM}=k\overrightarrow{e}\Rightarrow$ k là tọa độ của điểm M đối với trục $\left(O;\overrightarrow{e}\right)$.

+) $\overrightarrow{OM}=x\overrightarrow{i}+\text{y}\overrightarrow{\text{j}}\iff \overrightarrow{OM}=(x;y)\iff M(x;y)$

+) Cho điểm M (x; y) tùy ý trong mặt phẳng Oxy, nếu $M{M}_1\perp \text{O}x,M{M}_2\perp \text{Oy}$ thì $O{M}_1=x,O{M}_2=y$.

+) Tọa độ trung điểm M của đoạn thẳng AB: $x_M=\frac{x_A+x_B}{2};y_M=\frac{y_A+y_B}{2}$

+) Tọa độ trọng tâm G của tam giác ABC: $x_G=\frac{x_A+x_B+x_C}{3};y_G=\frac{y_A+y_B+y_C}{3}$

- Áp dụng các kiến thức về tọa độ vectơ trong mặt phẳng:

+) Cho hai điểm $A(x_A;y_A)$ và $B(x_B;y_B)$, khi đó $\overrightarrow{AB}=(x_B-x_A;y_B-y_A)$

+) Cho hai vectơ $\overrightarrow{u}=(x_1;y_1)$ và $\overrightarrow{v}=(x_2;y_2)$

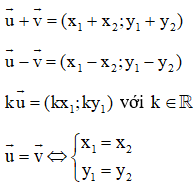
$\overrightarrow{u}$ cùng phương với vectơ $\overrightarrow{v}$ ($\overrightarrow{v}\ne \overrightarrow{0}$) khi và chỉ khi:

$$\begin{gathered} \overrightarrow{u}=k\overrightarrow{v}\iff \left\{\begin{array}{l}{x}_1=k{x}_2\\ y_1=k{y}_2\end{array}\right. \\ \iff \frac{x_1}{x_2}=\frac{y_1}{y_2}=k\iff x_1{y}_2=x_2{y}_1 \end{gathered}$$

Ví dụ minh họa:

Bài 1: Trong mặt phẳng Oxy, cho ba điểm A(3; 5), B(2; 4) và C(6; 1). Biết M là trung điểm của BC. Chứng minh ba điểm A, B, C tạo thành một tam giác. Tìm tọa độ điểm M và tọa độ trọng tâm G của tam giác ABC.

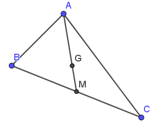
Lời giải:

Điểm M (x; y) là trung điểm của BC nên ta có:

Điểm G (x’; y’) là trọng tâm của tam giác ABC nên ta có:

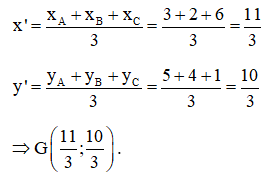
Bài 2: Trong mặt phẳng Oxy, cho ba điểm A, B, C không thẳng hàng biết A(1; 4) , B(3; 2) và C(6; 7). Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

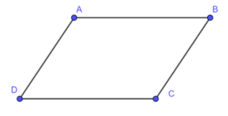
Lời giải:

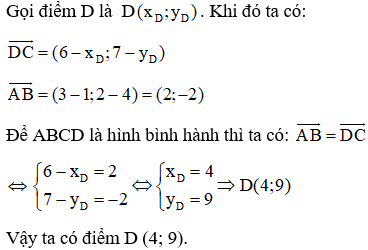
Dạng 2: Chứng minh một tính chất của một hình.

Phương pháp giải:

- Áp dụng kiến thức về tọa độ của điểm và vectơ trong mặt phẳng Oxy:

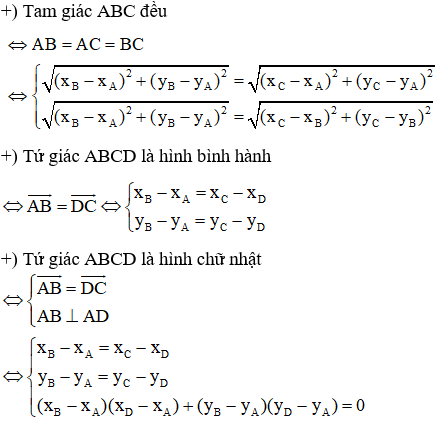
Ví dụ minh họa:

Bài 1: Chứng minh tính chất của các hình sau:

a) Chứng minh tam giác ABC là tam giác vuông cân tại A. Biết A(1; 1), B(1; 5) và C(5; 1) .

b) Biết rằng M(1; 1), N(7; 1) và P$\left(4;\sqrt{27}+1\right)$. Chứng minh tam giác MNP là tam giác đều.

c) Chứng minh tứ giác ABCD là hình bình hành biết A(-5; 6), B(-1; 6), C(-2; 4) và D(-6; 4)

Lời giải:

a)

Ta có:

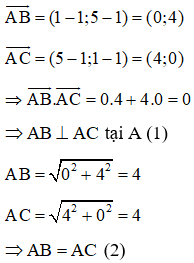
Từ (1) và (2) ta có tam giác ABC vuông cân tại A.

b)

Ta có:

c)

Ta có:

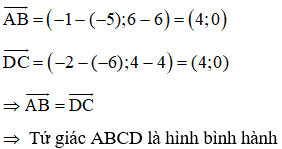
Bài 2: Chứng minh tính chất của các hình sau:

a) Chứng minh tứ giác MNPQ là hình chữ nhật. Biết M(-6; 6), N(-2; 6), P(-2; 4) và Q(-6; 4).

b) Chứng minh tứ giác ABCD là hình thoi. Biết A(-4; 7), B(-2; 6), C(-4; 5), và   D(-6; 6)

Lời giải:

a)

Ta có:

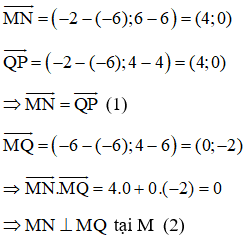
Từ (1) và (2) ta có tứ giác MNPQ là hình chữ nhật.

b)

Ta có:

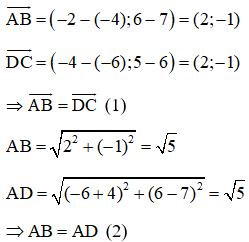
Từ (1) và (2) ta có tứ giác ABCD là hình thoi.

Dạng 3: Áp dụng phương pháp tọa độ chứng minh bất đẳng thức và tìm giá trị lớn nhất, nhỏ nhất.

Phương pháp giải:

- Khi gặp các bài toán đại số mà mỗi biểu thức dưới dấu căn bậc hai $\sqrt{A},\sqrt{B}$,… có thể biểu diễn dưới dạng:  $\sqrt{A}=\sqrt{{a_1}^2+{a_1}^2}$, $\sqrt{B}=\sqrt{{b_1}^2+{b_1}^2}$,… Ta thiết lập các điểm, các vectơ có tọa độ phù hợp sao cho độ dài các đoạn thẳng, các vectơ tương ứng có độ dài bằng $\sqrt{A},\sqrt{B}$,… rồi sử dụng các bất đẳng thức hình học cơ bản (bất đẳng thức về độ dài các cạnh trong tam giác, bất đẳng thức về độ dài đường gấp khúc,… ) và các bất đẳng thức về vectơ để giải quyết bài toán.

- Một số bất đẳng thức về vectơ:

(Dấu bằng xảy ra khi $\overrightarrow{u}$ và $\overrightarrow{v}$ ngược hướng)

Ví dụ minh họa:

Bài 1: Với mọi số thực x, chứng minh bất đẳng thức:

$\sqrt{x^2+2x+2}+\sqrt{x^2-2x+5}\ge \sqrt{13}$

Lời giải:

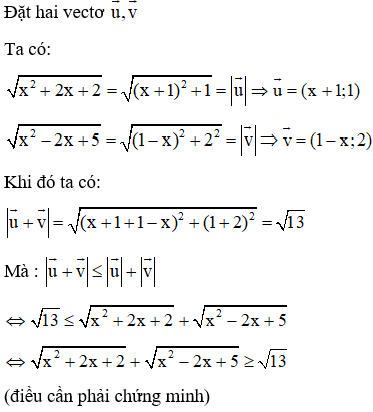
Bài 2: Cho x, y, z thỏa mãn $\left\{\begin{array}{l}{x}^2+xy+y^2=3\\ y^2+yz+z^2=16\end{array}\right.$. Tìm giá trị lớn nhất của biểu thức

A = xy + yz + xz.

Lời giải:

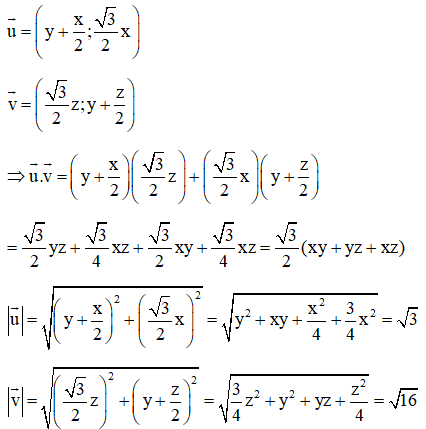
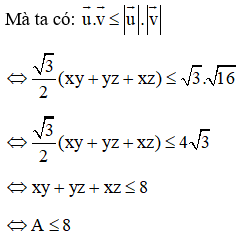
Vậy giá trị lớn nhất của A là 8.

C. Bài tập tự luyện.

Bài 1: Cho hai điểm A(3; 5), B(2; 5). Tìm tọa độ điểm C là trung điểm của AB.

Đáp số: $C\left(\frac{5}{2};5\right)$

Bài 2: Cho ba điểm A(2; 7), B(4; 7) và D(1; 3). Tìm điểm C sao cho ABCD là hình bình hành.

Đáp số: C(3; 3)

Bài 3: Cho hình chữ nhật ABCD tâm O. Tìm tọa độ tâm O của hình chữ nhật, biết A(3; 4), B(6; 4), C(6; -1) và D(3; -1).

Đáp số: $O\left(\frac{9}{2};\frac{3}{2}\right)$

Bài 4: Cho hình thoi ABCD cạnh a biết tâm A(1; 6), C(1; 8). Tìm tọa độ tâm O của hình thoi.

Đáp số: O(1; 7)

Bài 5: Cho tam giác ABC có trọng tâm G, biết G(2; 5), B(4; 6) và C(7; 9). Tìm tọa độ của điểm A.

Đáp số: A(-5; 0)

Bài 6: Cho điểm M(3; -4). Tìm tọa độ điểm M’ là hình chiếu vuông góc của M trên Ox.

Đáp số: M’(3; 0)

Bài 7: Cho hai điểm A(1; 2) và B(-2; 3), gọi B’ là điểm đối xứng với B qua A. Tìm tọa độ của B’.

Đáp số: B’(4; 1)

Bài 8: Cho tứ giác ABCD biết A(3; 4), B(3; 5), C(4; 5) và D(4; 4). Chứng minh ABCD là hình vuông.

Đáp số: Ta có: AB = AD = 1 và $\overrightarrow{AB}.\overrightarrow{AD}=0$ và  $\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow$ ABCD là hình vuông

Bài 9: Cho bất đẳng thức $\sqrt{{a_1}^2+{a_2}^2}+\sqrt{{b_1}^2+{b_2}^2}\ge \sqrt{{(a_1+b_1)}^2+{(a_2+b_2)}^2}$. Chứng minh và cho biết điều kiện để dấu bằng xảy ra.

Đáp số: Áp dụng $\left|\overrightarrow{u}+\overrightarrow{v}\right|\le \left|\overrightarrow{u}\right|+\left|\overrightarrow{v}\right|$, dấu bằng xảy ra khi $a_1{b}_2=a_2{b}_1$

Bài 10: Cho x, y $\in ℝ$. Tìm giá trị nhỏ nhất của biểu thức:

S = $\sqrt{x^2+4y^2+6x+9}+\sqrt{x^2+4y^2-2x-12y+10}$

Đáp số: $S_{\min }=5$.