Phương trình đường thẳng và cách giải bài tập – Toán lớp 10

Phương trình đường thẳng và cách giải bài tập – Toán lớp 10

A. Lí thuyết tổng hợp

1. Các vectơ của đường thẳng:

+) Vectơ chỉ phương: Vectơ $\overrightarrow{u}$ được gọi là vectơ chỉ phương của đường thẳng $\Delta$ nếu $\overrightarrow{u}\ne \overrightarrow{0}$ và giá của $\overrightarrow{u}$ song song hoặc trùng với $\Delta$.

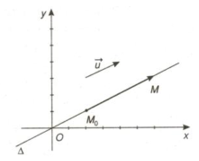
+) Vectơ pháp tuyến: Vectơ $\overrightarrow{n}$ được gọi là vectơ pháp tuyến của đường thẳng $\Delta$ nếu $\overrightarrow{n}\ne \overrightarrow{0}$ và $\overrightarrow{n}$ vuông góc với vectơ chỉ phương của $\Delta$.

+) Nhận xét:

- Nếu $\overrightarrow{u}$ là một vectơ chỉ phương của đường thẳng $\Delta$ thì k$\overrightarrow{u}$ ($k\ne 0$) cũng là một vectơ chỉ phương của $\Delta$.

- Nếu $\overrightarrow{n}$ là một vectơ pháp tuyến của đường thẳng $\Delta$ thì k$\overrightarrow{n}$ ($k\ne 0$) cũng là một vectơ pháp tuyến của $\Delta$.

- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương hoặc một vectơ pháp tuyến của đường thẳng đó.

- Một đường thẳng có vô số vectơ chỉ phương, vô số vectơ pháp tuyến.

2. Phương trình tổng quát của đường thẳng:

+) Định nghĩa: Phương trình $\Delta$: ax + by + c = 0 ($a^2+b^2\ne 0$)  là phương trình tổng quát của đường thẳng $\Delta$ nhận $\overrightarrow{n}$ (a; b) làm vectơ pháp tuyến.

+) Các dạng đặc biệt:

$\Delta$: ax + c = 0 , a$\ne 0\Rightarrow$ $\Delta$ song song với Oy hoặc trùng với Oy khi a = 1 và c = 0.

$\Delta$: ay + c = 0 , a$\ne 0\Rightarrow$ $\Delta$ song song với Ox hoặc trùng với Ox khi a = 1 và c = 0.

$\Delta$: ax + by = 0 ,$a^2+b^2\ne 0\Rightarrow$  $\Delta$ đi qua gốc tọa độ O(0; 0)

3. Phương trình tham số của đường thẳng:

+) Định nghĩa: Hệ $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\right.$, $a^2+b^2\ne 0$  là phương trình tham số của đường thẳng $\Delta$ đi qua điểm A$\left(x_0;y_0\right)$ và nhận vectơ $\overrightarrow{u}(a;b)$ làm vectơ chỉ phương, với t là tham số.

+) Chú ý:

Với mỗi $t\in ℝ$ thay vào phương trình tham số ta được một điểm M (x; y) $\in \Delta$

Một đường thẳng có vô số phương trình tham số.

- Phương trình chính tắc: $\frac{x-x_0}{a}=\frac{y-y_0}{b}$ ($a.b\ne 0$) là phương trình chính tắc của đường thẳng đi qua  điểm M$\left(x_0;y_0\right)$  và nhận  làm vectơ chỉ phương.

- Phương trình đoạn chắn: Đường thẳng  cắt hai trục Ox và Oy lần lượt tại hai điểm A (a; 0), B (0; b) với  có phương trình đoạn chắn là .

4. Hệ số góc:

Phương trình đường thẳng $\Delta$ đi qua điểm M$\left(x_0;y_0\right)$ có hệ số góc k thỏa mãn: $y-y_0=k(x-x_0)$

+ Nếu $\Delta$ có vectơ chỉ phương $\overrightarrow{u}=(u_1;u_2)$ với $u_1\ne 0$ thì hệ số góc của $\Delta$ là $k=\frac{u_2}{u_1}$

+ Nếu $\Delta$có hệ số góc k thì $\Delta$ có vectơ chỉ phương là $\overrightarrow{u}=(1;k)$

5. Vị trí tương đối của hai đường thẳng:

+) Xét hai đường thẳng $d_1:a_{1}x+b_{1}y+c_1=0$ và $d_2:a_{2}x+b_{2}y+c_2=0$ với ${a_1}^2+{b_1}^2\ne 0,{a_2}^2+{b_2}^2\ne 0$. Tọa độ giao điểm của hai đường thẳng đó là nghiệm của hệ phương trình:

$\left\{\begin{array}{l}{a}_{1}x+b_{1}y+c_1=0\\ a_{2}x+b_{2}y+c_2=0\end{array}\right.$  (1)

Ta có các trường hợp sau:

TH1: Hệ (1) có duy nhất một nghiệm  $\left(x_0;y_0\right)$$\Rightarrow d_1\cap d_2$  tại M  $\left(x_0;y_0\right)$

TH2: Hệ (1) có vô số nghiệm $\Rightarrow d_1$  trùng với $d_2$

TH3: Hệ (1) vô nghiệm $\Rightarrow d_1$ // $d_2$

+) Chú ý: Với $a_2,b_2,c_2\ne 0$ ta có:

$$\begin{gathered} d_1\cap d_2\iff \frac{a_1}{a_2}\ne \frac{b_1}{b_2} \\ {d}_1//d_2\iff \frac{a_1}{a_2}=\frac{b_1}{b_2}\ne \frac{c_1}{c_2} \\ {d}_1\equiv d_2\iff \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2} \end{gathered}$$

6. Góc giữa hai đường thẳng:

+ Cho hai đường thẳng $d_1:a_{1}x+b_{1}y+c_1=0$ có vectơ pháp tuyến $\overrightarrow{n_1}$ và $d_2:a_{2}x+b_{2}y+c_2=0$ có vectơ pháp tuyến $\overrightarrow{n_2}$ với ${a_1}^2+{b_1}^2\ne 0,{a_2}^2+{b_2}^2\ne 0$, góc giữa hai đường thẳng đó được kí hiệu là $(d_1,d_2)$,$(d_1,d_2)$  luôn nhỏ hơn hoặc bằng ${90}^o$. Đặt $\alpha =(d_1,d_2)$ ta có:

$\cos \alpha =\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{\left|a_1{a}_2+b_1{b}_2\right|}{\sqrt{{a_1}^2+{b_1}^2}.\sqrt{{a_2}^2+{b_2}^2}}$

+ Chú ý:

$d_1\perp d_2\iff \overrightarrow{n_1}\perp \overrightarrow{n_2}\iff a_1{a}_2+b_1{b}_2=0$

Nếu $d_1$ và $d_2$ có phương trình đường thẳng là $y=k_{1}x+m_1$ và $y=k_{2}x+m_2$ thì $d_1\perp d_2\iff k_1.k_2=-1$

7. Khoảng cách từ một điểm đến một đường thẳng:

Trong mặt phẳng Oxy cho đường thẳng $\Delta$ có phương trình ax + by + c = 0 và điểm M$\left(x_0;y_0\right)$. Khoảng cách từ điểm M đến đường thẳng $\Delta$ được kí hiệu là d (M, $\Delta$) và tính bằng công thức:

$d(M,\Delta )=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$

B. Các dạng bài.

Dạng 1: Cách viết các dạng phương trình đường thẳng.

Phương pháp giải:

a) Cách viết phương trình tổng quát của đường thẳng $\Delta$

+ Tìm vectơ pháp tuyến $\overrightarrow{n}(a;b)$ của đường thẳng $\Delta$

+ Tìm một điểm M$\left(x_0;y_0\right)$  thuộc $\Delta$

+ Viết phương trình $\Delta$ theo công thức: $a(x-x_0)+b(y-y_0)=0$

+ Biến đổi thành dạng ax + by + c = 0

Nếu đường thẳng ${\Delta }_1$ song song với đường thẳng ${\Delta }_2$: ax + by + c = 0 thì ${\Delta }_1$ có phương trình tổng quát ax + by + c’ = 0, c ≠ c’.

Nếu đường thẳng ${\Delta }_1$ vuông góc với đường thẳng ${\Delta }_2$: ax + by + c = 0 thì ${\Delta }_1$ có phương trình tổng quát -bx + ay + c’ = 0, c ≠ c’.

b) Cách viết phương trình tham số của đường thẳng $\Delta$

+ Tìm vectơ chỉ phương $\overrightarrow{u}=(u_1;u_2)$ của đường thẳng $\Delta$

+ Tìm một điểm M $\left(x_0;y_0\right)$ thuộc $\Delta$

+ Viết phương trình tham số: $\left\{\begin{array}{l}x=x_0+u_{1}t\\ y=y_0+u_{2}t\end{array}\right.$

Nếu $\Delta$ có hệ số góc k thì $\Delta$ có vectơ chỉ phương $\overrightarrow{u}=(1;k)$

Nếu $\Delta$ có vectơ pháp tuyến $\overrightarrow{n}(a;b)$  thì $\Delta$ có vectơ chỉ phương $\overrightarrow{u}=(-b;a)$ hoặc $\overrightarrow{u}=(b;-a)$ và ngược lại.

c) Cách viết phương trình chính tắc của đường thẳng $\Delta$. (chỉ áp dụng khi có vectơ chỉ phương $\overrightarrow{u}=(a;b)$ với $a.b\ne 0$)

+ Tìm vectơ chỉ phương $\overrightarrow{u}=(a;b)$ ($a.b\ne 0$) của đường thẳng $\Delta$

+ Tìm một điểm M $\left(x_0;y_0\right)$ thuộc $\Delta$

+ Viết phương trình chính tắc:  $\frac{x-x_0}{a}=\frac{y-y_0}{b}$

d) Cách viết phương trình đoạn chắn của đường thẳng $\Delta$ (chỉ áp dụng khi đường thẳng cắt hai trục Ox, Oy)

+ Tìm hai giao điểm của $\Delta$ với trục Ox, Oy lần lượt là A(a; 0), B(0; b)

+ Viết phương trình đoạn chắn $\frac{x}{a}+\frac{y}{b}=1$ ($a.b\ne 0$).

Ví dụ minh họa:

Bài 1: Cho đường thẳng d cắt trục Ox, Oy tại hai điểm A(0; 5) và B(6; 0). Viết phương trình tổng quát và phương trình đoạn chắn của đường thẳng d.

Lời giải:

Vì A(0; 5) và B(6; 0) thuộc đường thẳng d nên ta có $\overrightarrow{AB}$ là vectơ chỉ phương của đường thẳng d.

$\overrightarrow{AB}=(6-0;0-5)=(6;-5)$

 $\Rightarrow$Vectơ pháp tuyến của d là $\overrightarrow{n}=(5;6)$

Chọn điểm A(0; 5) thuộc đường thẳng d, ta có phương trình tổng quát của đường thẳng d:

5.(x – 0) + 6.(y – 5) = 0

$\iff$ 5x + 6y – 30 = 0

Vì đường thẳng d cắt trục Ox, Oy lần lượt tại hai điểm A(0; 5) và B(6; 0) nên ta có phương trình đoạn chắn: $\frac{x}{6}+\frac{y}{5}=1$ .

Bài 2: Cho đường thẳng d đi qua hai điểm M(5; 8) và N(3; 1). Viết phương trình tham số và phương trình chính tắc của đường thẳng d.

Lời giải:

Vì M(5; 8) và N(3; 1) thuộc đường thẳng d nên ta có $\overrightarrow{MN}$ là vectơ chỉ phương của đường thẳng d, có$\overrightarrow{MN}$ = (3 – 5; 1 – 8) = (-2; -7)

Chọn điểm N(3; 1) thuộc đường thẳng d ta có phương trình tham số của đường thẳng d:$\left\{\begin{array}{l}x=3-2t\\ y=1-7t\end{array}\right.$

Chọn điểm M(5; 8) thuộc đường thẳng d ta có phương trình chính tắc của đường thẳng d:$\frac{x-5}{-2}=\frac{y-8}{-7}$ 

Dạng 2: Vị trí tương đối giữa hai đường thẳng.

Phương pháp giải:

Áp dụng lí thuyết về vị trí tương đối giữa hai đường thẳng: $d_1:a_{1}x+b_{1}y+c_1=0$ và $d_2:a_{2}x+b_{2}y+c_2=0$ với ${a_1}^2+{b_1}^2\ne 0,{a_2}^2+{b_2}^2\ne 0$.

Tọa độ giao điểm của hai đường thẳng đó là nghiệm của hệ phương trình:

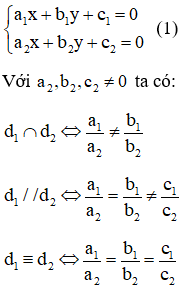
Ví dụ minh họa:

Bài 1: Xét vị trí tương đối của hai đường thẳng sau:

a) $d_1:4x-10y+1=0$ và $d_2:x+y+2=0$

b) $d_3:12x-6y+10=0$ và $d_4:2x-y+5=0$

c) $d_5:8x+10y-12=0$ và $d_6:4x+5y-6=0$.

Lời giải:

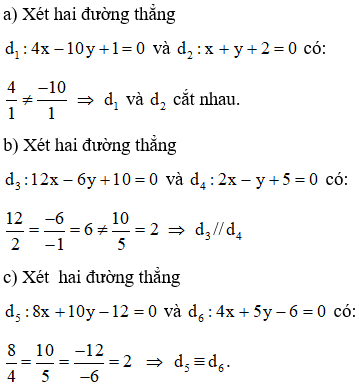
Bài 2: Cho hai đường thẳng: $d_1:x-2y+5=0$ và $d_2:3x-y=0$. Tìm tọa độ giao điểm của $d_1$ và $d_2$.

Lời giải:

Xét tỉ số: $\frac{1}{3}\ne \frac{-2}{-1}\Rightarrow d_1\cap d_2$ . Gọi tọa độ giao điểm của $d_1$ và $d_2$ là M(x; y) với x và y là nghiệm của hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{l}x-2y+5=0\\ 3x-y=0\end{array}\right.\iff \left\{\begin{array}{l}x-2y=-5\\ 3x-y=0\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1\\ y=3\end{array}\right. \end{gathered}$$

Vậy $d_1\cap d_2$ tại M (1; 3).

Dạng 3: Tính góc giữa hai đường thẳng.

Phương pháp giải:

Áp dụng lí thuyết về góc giữa hai đường thẳng:

- Cho hai đường thẳng $d_1:a_{1}x+b_{1}y+c_1=0$ có vectơ pháp tuyến $\overrightarrow{n_1}$ và $d_2:a_{2}x+b_{2}y+c_2=0$ có vectơ pháp tuyến $\overrightarrow{n_2}$ với ${a_1}^2+{b_1}^2\ne 0,{a_2}^2+{b_2}^2\ne 0$, góc giữa hai đường thẳng được kí hiệu là $(d_1,d_2)$, $(d_1,d_2)$ luôn nhỏ hơn hoặc bằng ${90}^o$ Đặt $\alpha =(d_1,d_2)$ ta có:

$\cos \alpha =\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{\left|a_1{a}_2+b_1{b}_2\right|}{\sqrt{{a_1}^2+{b_1}^2}.\sqrt{{a_2}^2+{b_2}^2}}$

- Chú ý:

$d_1\perp d_2\iff \overrightarrow{n_1}\perp \overrightarrow{n_2}\iff a_1{a}_2+b_1{b}_2=0$

$d_1\perp d_2\iff \overrightarrow{u_1}\perp \overrightarrow{u_2}\iff x_1{x}_2+y_1{y}_2=0$ với $\overrightarrow{u_1}=(x_1;y_1)$ là vectơ chỉ phương của $d_1$, $\overrightarrow{u_2}=(x_2;y_2)$ là vectơ chỉ phương của $d_2$.

Nếu $d_1$ và $d_2$ có phương trình đường thẳng là $y=k_{1}x+m_1$ và $y=k_{2}x+m_2$ thì $d_1\perp d_2\iff k_1.k_2=-1$

Ví dụ minh họa:

Bài 1: Cho hai đường thẳng $d:\left\{\begin{array}{l}x=7-2t\\ y=5-t\end{array}\right.$ và d’$\left\{\begin{array}{l}x=1+t\text{'}\\ y=2+3t\text{'}\end{array}\right.$: . Xác định số đo góc giữa d và d’.

Lời giải:

Xét $d:\left\{\begin{array}{l}x=7-2t\\ y=5-t\end{array}\right.$ ta có vectơ chỉ phương của d là $\overrightarrow{u}$ = (-2; -1)

$\Rightarrow$ Vectơ pháp tuyến của d là  = (1; -2).

Xét d’: $\left\{\begin{array}{l}x=1+t\text{'}\\ y=2+3t\text{'}\end{array}\right.$ ta có vectơ chỉ phương của d’ là $\overrightarrow{u\text{'}}$ = (1; 3)

$\Rightarrow$ Vectơ pháp tuyến của d’ là  $\overrightarrow{n}$= (-3; 1).

Ta có:

$$\begin{gathered} \cos (d,d\text{'})=\left|\cos (\overrightarrow{n},\overrightarrow{n\text{'}})\right| \\ =\frac{\left|-2.1+(-1).3\right|}{\sqrt{{(-2)}^2+1^2}.\sqrt{{(-1)}^2+3^2}} \\ =\frac{5}{5\sqrt{2}}=\frac{1}{\sqrt{2}} \end{gathered}$$

Góc giữa hai đường thẳng luôn nhỏ hơn hoặc bằng ${90}^o\Rightarrow (d,d\text{'})={45}^o$.

Bài 2: Cho hai đường thẳng d: 4x – 2y + 6 = 0 và d’: x + 2y + 1 = 0. Xác định số đo góc giữa d và d’.

Lời giải:

Xét d: 4x – 2y + 6 = 0 ta có vectơ pháp tuyến của d là  $\overrightarrow{n}$= (4; -2)

Xét d’: x + 2y + 1 = 0 ta có vectơ pháp tuyến của d’ là  $\overrightarrow{n\text{'}}$= (1; 2)

Ta có: $\overrightarrow{n}$. $\overrightarrow{n\text{'}}$= 4.1 + (-2).2 = 0

$$\begin{gathered} \Rightarrow d\perp d\text{'} \\ \Rightarrow (d,d\text{'})={90}^o \end{gathered}$$

Dạng 4: Khoảng cách từ một điểm đến một đường thẳng.

Phương pháp giải:

Áp dụng lí thuyết về khoảng cách từ một điểm đến một đường thẳng: Trong mặt phẳng Oxy, đường thẳng $\Delta$ có phương trình ax + by + c = 0 và điểm M$\left(x_0;y_0\right)$ . Khoảng cách từ điểm M đến đường thẳng $\Delta$ được kí hiệu là d (M, $\Delta$), tính bằng công thức:

$d(M,\Delta )=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$

Ví dụ minh họa:

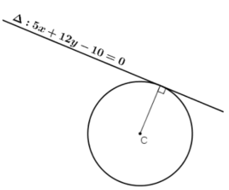
Bài 1: Tìm bán kính của đường tròn tâm C(-2; -2) . Biết đường tròn tiếp xúc với đường thẳng $\Delta$ : 5x + 12y -10 = 0.

Lời giải:

Vì đường tròn tiếp xúc với đường thẳng  $\Delta$: 5x + 12y – 10 = 0 nên ta có bán kính của đường tròn bằng khoảng từ tâm C đến đường thẳng $\Delta$. Ta có:

$$\begin{gathered} R=d(C,\Delta ) \\ =\frac{\left|5.(-2)+12(-2)-10\right|}{\sqrt{5^2+{12}^2}}=\frac{44}{13} \end{gathered}$$

Bài 2: Cho điểm A (3; 6). Tìm khoảng cách từ A đến đường thẳng d: $\left\{\begin{array}{l}x=4-3t\\ y=7+2t\end{array}\right.$

Lời giải:

Xét đường thẳng d: $\left\{\begin{array}{l}x=4-3t\\ y=7+2t\end{array}\right.$ ta có vectơ chỉ phương của d là $\overrightarrow{u}$ = (-3; 2)

 $\Rightarrow$vectơ pháp tuyến của d là $\overrightarrow{n}$ = (2; 3)

Chọn điểm M (4; 7) thuộc d ta có phương trình tổng quát của d là:

2.(x – 4) + 3.(y – 7) = 0

$\iff$ 2x – 8 + 3y – 21 = 0

$\iff$2x + 3y – 29 = 0

Khoảng cách từ A (3; 6) đến đường thẳng d là:

$d(A,d)=\frac{\left|2.3+3.6-29\right|}{\sqrt{2^2+3^2}}=\frac{5}{\sqrt{13}}$

C. Bài tập tự luyện.

Bài 1: Viết phương trình tổng quát của đường thẳng d biết d đi qua 2 điểm A (3; 5) và B (4; 6).

Đáp án: d: - x + y = 2

Bài 2: Viết phương trình tham số của đường thẳng d’ biết d’ đi qua 2 điểm A (2; 7) và B (0; 5).

Đáp án: d’: $\left\{\begin{array}{l}x=2-2t\\ y=7-2t\end{array}\right.$

Bài 3: Viết phương trình chính tắc của đường thẳng d đi qua hai điểm M (1; 6) và N (2; 3)

Đáp án: d: $\frac{x-1}{1}=\frac{y-6}{-3}$

Bài 4: Viết phương trình đoạn chắn của đường thẳng d biết d song song với đường thẳng d’: 4x – 3y + 2 = 0 và d đi qua điểm (2; 3)

Đáp án: d: 4x - 3y + 1 = 0

Bài 5: Xét vị trí tương đối giữa đường thẳng d: 3x – 5y + 2 = 0 và đường thẳng   d’: 3x – 5y = 0.

Đáp án: d // d’

Bài 6: Cho đường thẳng d: 2x – 6y + 3 = 0 và đường thẳng d’: x – m + 7 = 0. Tìm m để d // d’.

Đáp án: m = 3

Bài 7: Cho hai đường thẳng d: 6x – y = 0 và d’: 2x + 8y – 1 = 0. Tìm tọa độ giao điểm I của d và d’.

Đáp số: I $\left(\frac{1}{50};\frac{3}{25}\right)$

Bài 8: Cho hai đường thẳng d: 8x – 3y + 2 = 0 và d’: x = 4. Tìm số đo góc giữa d và d’.

Đáp án: $(d,d\text{'})={20}^{o}33\text{'}$

Bài 9: Cho điểm A (4; 7) và đường thẳng d’: x – 6 = 0. Tìm khoảng cách từ A đến đường thẳng d.

Đáp án: d (A, d’) = 2

Bài 10: Cho đường thẳng d: $\left\{\begin{array}{l}x=2+2t\\ y=3+t\end{array}\right.$. Tìm m để khoảng cách giữa A (2; m) và  đường thẳng d là 5.

Đáp số: $m=\frac{3-5\sqrt{5}}{2}$