Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto (2024) chi tiết nhất

Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto lớp 10 chi tiết nhất - Toán lớp 10

A. Lí thuyết tóm tắt.

- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:

$\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$ ( M tùy ý )

$\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$

- Quy tắc trọng tâm: Với G là trọng tâm tam giác ABC thì ta có:

$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$ ( M tùy ý )

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

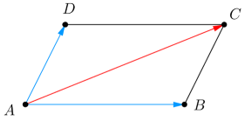
- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

B. Các công thức.

- Quy tắc trung điểm: I là trung điểm của AB

$\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$

$\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$ ( M tùy ý )

- Quy tắc trọng tâm: G là trọng tâm tam giác ABC

$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$ ( M tùy ý )

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

- Quy tắc hình hình hành: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ ( ABCD là hình bình hành )

C. Ví dụ minh họa.

Bài 1: Cho tam giác ABC vuông cân tại A. Có đường cao AH, G là trọng tâm của tam giác ABC, biết AB = AC = a. Tính độ dài vectơ $\overrightarrow{HC}+\overrightarrow{HB}$, $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}$.

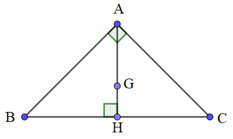
Giải:

Vì G là trọng tâm tam giác ABC nên ta áp dụng quy tắc trọng tâm có:

$$\begin{gathered} \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0} \\ \Rightarrow \left|\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|\overrightarrow{0}\right|=0 \end{gathered}$$

Vì tam giác ABC vuông cân tại A nên đường cao AH cũng là đường trung tuyến.

$\Rightarrow$H là trung điểm của BC.

Áp dụng quy tắc trung điểm cho đoạn BC ta có: $\overrightarrow{HC}+\overrightarrow{HB}=\overrightarrow{0}$

$\Rightarrow \left|\overrightarrow{HC}+\overrightarrow{HB}\right|=\left|\overrightarrow{0}\right|=0$

Bài 2: Cho hình bình hành ABCD. Biết AC = 2a. Tính độ dài vectơ $\overrightarrow{AB}+\overrightarrow{AD}$.

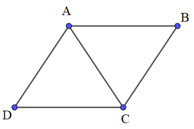
Giải:

Vì ABCD là hình bình hành nên ta áp dụng quy tắc hình bình hành có:

$$\begin{gathered} \overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC} \\ \Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC=2a \end{gathered}$$

Bài 3. Cho 3 điểm A, B, C không thẳng hàng. Có E là trung điểm của AB, F là trọng tâm của tam giác ABC, điểm M nằm ngoài AB và khác C.Biết ME = a và MF = 2a.Tính độ dài các vectơ sau: $\overrightarrow{MA}+\overrightarrow{MB}$, $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$.

Giải:

Vì E là trung điểm của AB nên ta áp dụng quy tắc trung điểm có:

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{ME} \\ \Rightarrow \left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|2\overrightarrow{ME}\right|=2.a=2a \end{gathered}$$

Vì F là trọng tâm của tam giác ABC nên ta áp dụng quy tắc trọng tâm có:

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MF} \\ \left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MF}\right|=3.2a=6a \end{gathered}$$

D. Bài tập tự luyện.

Bài 1: Cho hình vuông ABCD tâm O cạnh a. Tính độ dài các vectơ $\overrightarrow{OA}+\overrightarrow{OC}$ và $\overrightarrow{DA}+\overrightarrow{DC}$.

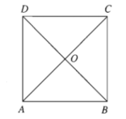
Bài 2: Cho tam giác đều MNE . Biết G là trọng tâm của tam giác MNE, điểm A tùy ý nằm ngoài tam giác MNE và AG = 2a. Tính độ dài các vecto $\overrightarrow{GM}+\overrightarrow{GN}+\overrightarrow{GE}$ và $\overrightarrow{AN}+\overrightarrow{AM}+\overrightarrow{AE}$.

Bài 3: Cho hình chữ nhật ABCD tâm O. Biết OA = a. Chứng minh rằng $\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{BA}+\overrightarrow{BC}\right|=2a$.

Xem thêm tổng hợp công thức môn Toán lớp 10 đầy đủ và chi tiết khác:

Trọn bộ công thức cơ bản về Vectơ dầy đủ

Công thức về tổng và hiệu hai vectơ chi tiết nhất

Công thức Phân tích vectơ lớp 10 chi tiết nhất

Công thức về Hệ trục tọa độ lớp 10 chi tiết nhất

Công thức góc giữa hai vectơ chi tiết nhất