Giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập (2024) chi tiết nhất

Giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập – Toán lớp 10

A. Lí thuyết.

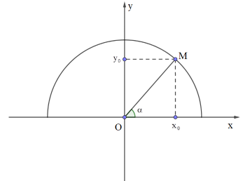
- Định nghĩa: Cho góc $\alpha$ ($0^o\le \alpha \le {180}^o$) bất kì, xác định một điểm $M(x_0;y_0)$ trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$. Khi đó ta có: $\sin \alpha =y_0$; $\cos \alpha =x_0$; $\tan \alpha =\frac{y_0}{x_0}\left(x_0\ne 0\right)$; $\cot \alpha =\frac{x_0}{y_0}\left(y_0\ne 0\right)$. ( sin, cos, tan, cot là các giá trị lượng giác của góc $\alpha$)

- Tính chất:

Hai góc bù nhau là hai góc có tổng bằng ${180}^o$. Cho góc $\alpha$ ta có:

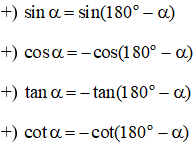
Hai góc phụ nhau là hai học có tổng bằng ${90}^o$. Cho góc $\alpha$ ta có:

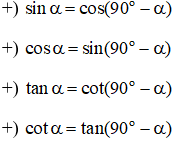
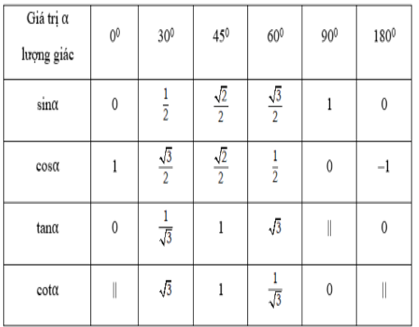
- Bảng giá trị lượng giác của các góc đặc biệt:

- Định nghĩa góc giữa hai vectơ: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$. Từ điểm O bất kì vẽ $\overrightarrow{OA}=\overrightarrow{a}$, $\overrightarrow{OB}=\overrightarrow{b}$, khi đó góc $\widehat{AOB}$ ($0^o\le \widehat{AOB}\le {180}^o$) là góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$. Kí hiệu: $\left(\overrightarrow{a},\overrightarrow{b}\right)$.

- Các hệ thức cơ bản liên hệ giữa các giá trị lượng giác :

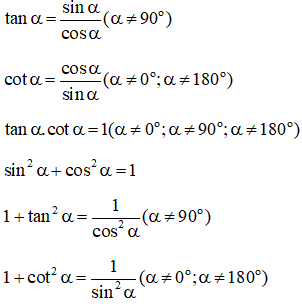
- Chú ý:

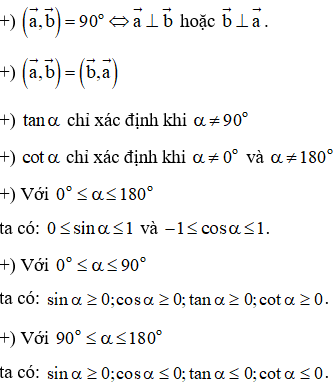
B. Các dạng bài.

Dạng 1: Góc và dấu của các giá trị lượng giác.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.

Ví dụ minh họa:

Bài 1: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {90}^o$. Xác định dấu của các giá trị lượng giác sau: $\sin (\alpha +{90}^o)$; $\cos \alpha$; $\tan (\alpha +{90}^o)$.

Lời giải:

Ta có:

$0^o\le \alpha \le {90}^o\Rightarrow {90}^o\le \alpha +{90}^o\le {180}^o$

Khi $0^o\le \alpha \le {90}^o$, ta có: $\cos \alpha \ge 0\Rightarrow \cos \alpha$ mang dấu dương hoặc bằng 0.

Khi ${90}^o\le \alpha +{90}^o\le {180}^o$ ta có:$\sin (\alpha +{90}^o)\ge 0$ ; $\tan (\alpha +{90}^o)\le 0$

$\sin (\alpha +{90}^o)$ mang dấu dương hoặc bằng 0 và $\tan (\alpha +{90}^o)$ mang dấu âm hoặc bằng 0.

Bài 2: Trên đường tròn đơn vị cho điểm $M\left(\frac{\sqrt{3}}{2};\frac{1}{2}\right)$. Xác định góc $\widehat{xOM}$.

Lời giải:

Điểm $M\left(\frac{\sqrt{3}}{2};\frac{1}{2}\right)\Rightarrow \sin \widehat{\text{x}OM}=\frac{1}{2}$; $\cos \widehat{xOM}=\frac{\sqrt{3}}{2}$

Dựa vào các giá trị lượng giác đặc biệt ta suy ra $\widehat{xOM}={30}^o$.

Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.

Ví dụ minh họa:

Bài 1: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {180}^o$ biết $\cos \alpha =\frac{-2}{3}$, hãy tính các giá trị lượng giác $\sin \alpha ,\cot \alpha ,\tan \alpha$.

Lời giải:

Áp dụng các hệ thức cơ bản liên hệ giữa các giá trị lượng giác ta có:

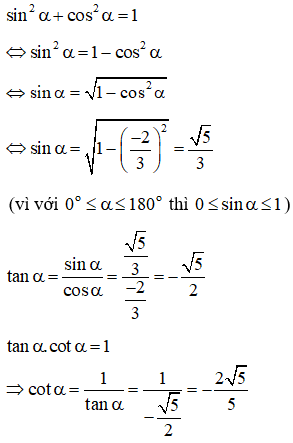
Bài 2: Cho góc thỏa mãn $0^o\le \alpha \le {90}^o$ , biết $\tan \alpha =2$. Tính các giá trị lượng giác $\cot \alpha ,\cos \alpha ,\sin \alpha$.

Lời giải:

Áp dụng các hệ thức cơ bản liên hệ giữa các giá trị lượng giác ta có:

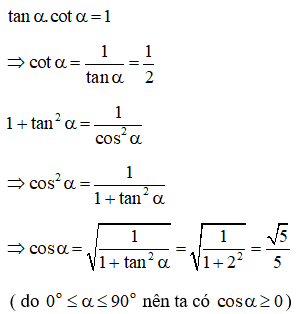
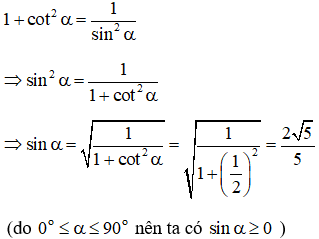
Dạng 3: Chứng minh, rút gọn một biểu thức lượng giác.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).

Ví dụ minh họa:

Bài 1: Chứng minh đẳng thức:

$a^2\sin {90}^o+b^2\cos {90}^o+c^2\cos {180}^o=(a-c)(a+c)$

Lời giải:

Theo bảng các giá trị lượng giác đặc biệt ta có:

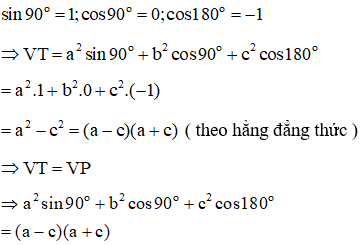
(điều cần phải chứng minh)

Bài 2: Rút gọn và tính giá trị biểu thức sau:

$A={\sin }^2{45}^o+{\cos }^2{45}^o+{\sin }^2{50}^o+{\sin }^2{40}^o+4\tan {55}^o\cot {55}^o$

Lời giải:

$$\begin{gathered} A={\sin }^2{45}^o+{\cos }^2{45}^o+{\sin }^2{50}^o \\ +{\sin }^2{40}^o+4\tan {55}^o\cot {55}^o \\ =({\sin }^2{45}^o+{\cos }^2{45}^o) \\ + ({\sin }^2{50}^o+{\sin }^2{40}^o)+4\tan {55}^o\cot {55}^o \end{gathered}$$

Ta có: $\sin {50}^o=\cos {40}^o$ (tính chất hai góc phụ nhau)

Áp dụng hệ thức liên hệ giữa các giá trị lượng giác ta có:

$$\begin{gathered} {\sin }^2{45}^o+{\cos }^2{45}^o=1 \\ {\cos }^2{40}^o+{\sin }^2{40}^o=1 \\ \tan {55}^o.\cot {55}^o=1 \\ \Rightarrow A=({\sin }^2{45}^o+{\cos }^2{45}^o) \\ +({\sin }^2{40}^o+{\sin }^2{40}^o)+4\tan {55}^o\cot {55}^o \\ \Rightarrow A=1+1+4.1=6 \end{gathered}$$

C. Bài tập tự luyện.

Bài 1: Cho góc $\alpha ={54}^o$. Nhận định nào sau đây là đúng ?

A. $\sin \alpha <0$

B. $\tan \alpha <0$

C. $\cos \alpha >0$

D. $\cot \alpha <0$

Đáp án: C

Bài 2: Cho biết $\sin \alpha >0;\cos \alpha <0$. Góc $\alpha$ có thể là góc nào sau đây:

A. $\alpha ={50}^o$

B. $\alpha ={45}^o$

C. $\alpha =0^o$

D. $\alpha ={112}^o$

Đáp án: D

Bài 3: Cho điểm M (1;0) trên đường tròn đơn vị. Hãy xác định số đo của góc $\widehat{xOM}$.

Đáp án: $\widehat{xOM}=0^o$

Bài 4: Cho góc $\alpha$ thỏa mãn ${10}^o\le \alpha \le {80}^o$. Hãy xác định dấu của các giá trị lượng giác $\sin (\alpha +{90}^o)$,$\cos \alpha$ .

Đáp án: $\sin (\alpha +{90}^o)$ mang dấu dương, $\cos \alpha$ mang dấu dương

Bài 5: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {180}^o$ biết $\cos \alpha =\frac{1}{2}$, hãy tính các giá trị lượng giác $\sin \alpha ,\cot \alpha ,\tan \alpha$.

Đáp án:

$\sin \alpha =\frac{\sqrt{3}}{2};\tan \alpha =\sqrt{3};\cot \alpha =\frac{1}{\sqrt{3}}$

Bài 6: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {180}^o$ biết $\cot \alpha =3$, hãy tính các giá trị lượng giác $\sin \alpha ,\cos \alpha ,\tan \alpha$.

Đáp án:

$\sin \alpha =\frac{\sqrt{10}}{10};\tan \alpha =\frac{1}{3};\cos \alpha =\frac{3\sqrt{10}}{10}$

Bài 7: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {90}^o$, biết $\cos \alpha -\sin \alpha =\frac{1}{2}$. Tính các giá trị lượng giác $\tan \alpha ,\cot \alpha$.

Đáp án: $\tan \alpha =\frac{4-\sqrt{7}}{3};\cot \alpha =\frac{4+\sqrt{7}}{3}$

Bài 8: Chứng minh đẳng thức: $\frac{1+\cot \alpha }{1-\cot \alpha }=\frac{\tan \alpha +1}{\tan \alpha -1}$.

Đáp án:

$VT=\frac{1+\cot \alpha }{1-\cot \alpha }=\frac{1+\frac{1}{\tan \alpha }}{1-\frac{1}{\tan \alpha }}=\frac{\tan \alpha +1}{\tan \alpha -1}=VP$

Bài 9: Chứng minh đẳng thức: $\frac{\sin \alpha +\cos \alpha }{{\cos }^3\alpha }={\tan }^3\alpha +{\tan }^2\alpha +\tan \alpha +1$.

Đáp án:

$$\begin{gathered} VT=\frac{\sin \alpha +\cos \alpha }{{\cos }^3\alpha }=\frac{\sin \alpha }{\cos \alpha }.\frac{1}{{\cos }^2\alpha }+\frac{1}{{\cos }^2\alpha } \\ ={\tan }^3\alpha +{\tan }^2\alpha +\tan \alpha +1=VP \end{gathered}$$

Bài 10: Rút gọn và tính giá trị biểu thức: $B={\sin }^2{15}^o+{\sin }^2{3}^o+{\sin }^2{75}^o+{\sin }^2{87}^o$

Đáp án: B = 2