Công thức giải bất phương trình một ẩn (2024) chi tiết nhất

Công thức giải bất phương trình một ẩn chi tiết nhất - Toán lớp 10

I. Lí thuyết tổng hợp.

- Bất phương trình một ẩn: Bất phương trình ẩn x là mệnh đề chứa biến có dạng f(x) < g(x) (f(x) $\le$ g(x)) (1). Trong đó f(x) và g(x) là những biểu thức của x. Ta gọi f(x) và g(x) lần lượt là vế trái và vế phải của bất phương trình (1). Số thực $x_0$ sao cho f($x_0$) < g($x_0$) (f($x_0$) $\le$ g($x_0$)) là mệnh đề đúng được gọi là một nghiệm của bất phương trình (1). Bất phương trình (1) cũng có thể viết lại dưới dạng như sau g(x) > f(x) (g(x) $\ge$ f(x))

- Giải bất phương trình là tìm tập nghiệm của nó, khi tập nghiệm rỗng thì ta nói bất phương trình vô nghiệm.

- Điều kiện xác định của một bất phương trình: Tương tự đối với phương trình, ta gọi các điều kiện của ẩn số x để f(x) và g(x) có nghĩa là điều kiện xác định (gọi tắt là điều kiện) của bất phương trình (1).

- Bất phương trình chứa tham số: Trong một bất phương trình, ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem như những hằng số và được gọi là tham số. Giải và biện luận bất phương trình chứa tham số là xét xem với các giá trị nào của tham số bất phương trình vô nghiệm, có nghiệm và tìm nghiệm đó.

- Bất phương trình tương đương: Hai bất phương trình có cùng tập nghiệm (có thể rỗng) là hai bất phương trình tương đương và dùng kí hiệu “$\iff$” để chỉ sự tương đương của hai bất phương trình đó.

- Phép biến đổi bất phương trình tương đương: Để giải một bất phương trình ta liên tiếp biến đổi nó thành những bất phương trình tương đương cho đến khi được bất phương trình đơn giản có thể viết ngay tập nghiệm. Các phép biến đổi như vậy được gọi là các phép biến đổi tương đương.

- Các phép biến đổi tương đương:

+ Cộng (trừ): Cộng (trừ) hai vế của bất phương trình với cùng một biểu thức mà không làm thay đổi điều kiện của bất phương trình thì ta được một bất phương trình tương đương.

+ Nhân (chia): Nhân (chia) hai vế của bất phương trình với cùng một biểu thức luôn nhận giá trị dương (mà không làm thay đổi điều kiện của bất phương trình) ta được một bất phương trình tương đương. Nhân (chia) hai vế của bất phương trình với cùng một biểu thức luôn nhận giá trị âm (mà không làm thay đổi điều kiện của bất phương trình) và đổi chiều bất phương trình ta được một bất phương trình tương đương.

+ Bình phương: Bình phương hai vế của một bất phương trình có hai vế không âm mà không làm thay đổi điều kiện của nó ta được một bất phương trình tương đương.

- Chú ý:

+ Khi biến đổi các biểu thức ở hai vế của một bất phương trình thì điều kiện của bất phương trình có thể bị thay đổi. Để tìm nghiệm của một bất phương trình ta phải tìm các giá trị x thỏa mãn điều kiện của bất phương trình đó và là nghiệm của bất phương trình mới.

+ Khi nhân (chia) hai vế của bất phương trình với biểu thức mới, ta cần lưu ý đến điều kiện về dấu của biểu thức đó. Nếu biểu thức nhận cả giá trị dương lẫn giá trị âm thì ta phải lần lượt xét từng trường hợp.

+ Khi giải bất phương trình mà phải bình phương hai vế thì ta xét hai trường hợp:

TH1: Hai vế cùng có giá trị không âm

TH2: Hai vế cùng có giá trị âm

II. Các công thức.

Cho P(x), Q(x) và f(x) là các biểu thức ẩn x.

P(x) < Q(x) $\iff$ P(x) + f(x) < Q(x) + f(x)

P(x) < Q(x) + f(x) $\iff$ P(x) – f(x) < Q(x)

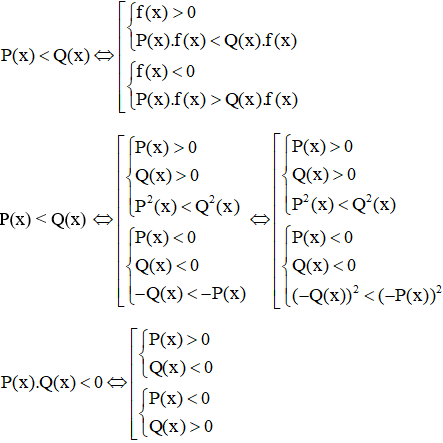
(tương tự với phép chia)

$P\left(x\right).Q\left(x\right)>0\iff \left[\begin{array}{l}\left\{\begin{array}{l}P\left(x\right)>0\\ Q\left(x\right)>0\end{array}\right.\\ \left\{\begin{array}{l}P\left(x\right)<0\\ Q\left(x\right)<0\end{array}\right.\end{array}\right.$

(tương tự với phép chia)

III. Ví dụ minh họa.

Bài 1: Giải bất phương trình: $-2x+\frac{3}{5}>2x-7$.

Lời giải:

$$\begin{gathered} -2x+\frac{3}{5}>2x-7 \\ \iff -2x-2x>\frac{-3}{5}-7 \\ \iff -4x>\frac{-3}{5}-7 \\ \iff 4x<7+\frac{3}{5} \\ \iff 4x<\frac{38}{5} \\ \iff x<\frac{19}{10} \end{gathered}$$

Vậy bất phương trình có tập nghiệm $S=\left(-\infty ;\frac{19}{10}\right)$.

Bài 2: Giải bất phương trình: (2x – 7)(4 – 5x) > 0.

Lời giải:

Ta có: (2x – 7)(4 – 5x) > 0

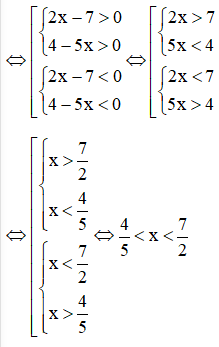
Vậy tập nghiệm của bất phương trình là $S=\left(\frac{4}{5};\frac{7}{2}\right)$.

Bài 3: Giải bất phương trình $\frac{3x-4}{x-2}>0$.

Lời giải:

Điều kiện xác định của bất phương trình là $x\ne 2$

Ta có: $\frac{3x-4}{x-2}>0$

$$\begin{gathered} \iff \left[\begin{array}{l}\left\{\begin{array}{l}3x-4>0\\ x-2>0\end{array}\right.\\ \left\{\begin{array}{l}3x-4<0\\ x-2<0\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}\left\{\begin{array}{l}3x>4\\ x>2\end{array}\right.\\ \left\{\begin{array}{l}3x<4\\ x<2\end{array}\right.\end{array}\right. \\ \iff \left[\begin{array}{l}\left\{\begin{array}{l}x>\frac{4}{3}\\ x>2\end{array}\right.\\ \left\{\begin{array}{l}x<\frac{4}{3}\\ x<2\end{array}\right.\end{array}\right. \end{gathered}$$

$\iff \left[\begin{array}{l}x>2\\ x<\frac{4}{3}\end{array}\right.$ (thỏa mãn điều kiện xác định)

Vậy tập nghiệm của bất phương trình là $S=\left(-\infty ;\frac{4}{3}\right)\cup \left(2;+\infty \right)$.

IV. Bài tập tự luyện.

Bài 1: Giải bất phương trình: $\frac{2x-5}{2-x}\ge -1$.

Bài 2: Giải bất phương trình: $\frac{5(x-1)}{6}-1<\frac{2(x+1)}{3}$.

Xem thêm tổng hợp công thức môn Toán lớp 10 đầy đủ và chi tiết khác:

Các tính chất của bất đẳng thức lớp 10 đầy đủ, chi tiết

Bất đẳng thức Cô-si và hệ quả chi tiết nhất

Bất đẳng thức chứa dấu giá trị tuyệt đối chi tiết nhất

Dấu của nhị thức bậc nhất chi tiết nhất

Công thức giải bất phương trình chứa dấu giá trị tuyệt đối chi tiết nhất