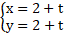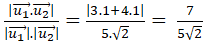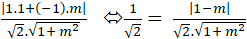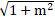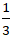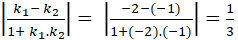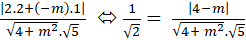Công thức tính góc giữa hai đường thẳng (2024) các dạng bài tập và cách giải

Công thức tính góc giữa hai đường thẳng hay, chi tiết nhất - Toán lớp 10

I. Lý thuyết góc giữa hai đường thẳng

1. Góc giữa hai đường thẳng là gì?

- Góc giữa hai đường thẳng là góc $\alpha$ được tạo bởi hai đường thẳng d và d’ có số đo $0^o\le \alpha \le {90}^o$. Khi d song song hoặc trùng với d’, ta quy ước góc giữa chúng bằng $0^o$.

- Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương hoặc hai vectơ pháp tuyến của chúng.

2. Cách xác định góc giữa hai đường thẳng

Để xác định góc giữa hai đường thẳng a và b, ta lấy điểm O thuộc 1 trong 2 đương thẳng sau đó vẽ 1 đường thẳng đi qua O và song song với 2 đường còn lại.

Nếu vector u là vector chỉ phương của đường thẳng a, đồng thời vector v là vector chỉ phương của đường thẳng b, góc giữa (u, v) = $\alpha$ thì ta có thể suy ra góc giữa 2 đường thẳng a và b bằng $\alpha$ ($0°\le \alpha \le 90°$)

II. Công thức góc giữa hai đường thẳng

- Cho hai đường thẳng d và d’ có vectơ chỉ phương lần lượt là: $\overrightarrow{u}=(a;b)$ và $\overrightarrow{u\text{'}}=(a\text{'};b\text{'})$. Góc giữa hai đường thẳng được xác định bởi:

$\cos (d,d\text{'})=\left|cos(\overrightarrow{u},\overrightarrow{u\text{'}})\right|=\frac{\left|a.a\text{'}+b.b\text{'}\right|}{\sqrt{a^2+b^2}.\sqrt{a{\text{'}}^2+b{\text{'}}^2}}$

- Cho hai đường thẳng d và d’ có vectơ pháp tuyến lần lượt là: $\overrightarrow{n}=(a;b)$ và $\overrightarrow{n\text{'}}=(a\text{'};b\text{'})$. Góc giữa hai đường thẳng được xác định bởi:

$\cos (d,d\text{'})=\left|cos(\overrightarrow{n},\overrightarrow{n\text{'}})\right|=\frac{\left|a.a\text{'}+b.b\text{'}\right|}{\sqrt{a^2+b^2}.\sqrt{a{\text{'}}^2+b{\text{'}}^2}}$

- Gọi k và k’ lần lượt là hệ số góc của hai đường thẳng d và d’. Ta có:

$\tan (d,d\text{'})=\left|\frac{k-k\text{'}}{1+k.k\text{'}}\right|$

III. Ví dụ minh họa

Bài 1: Tính góc giữa hai đường thẳng d: 3x + y - 2 = 0 và d’: 2x - y + 3 = 0.

Lời giải:

Hai đường thẳng d và d’ có các vectơ pháp tuyến lần lượt là: $\overrightarrow{n}=(3;1)$ và $\overrightarrow{n\text{'}}=(2;-1)$. Ta có:

$$\begin{gathered} \cos (d,d\text{'})=\left|cos(\overrightarrow{n},\overrightarrow{n\text{'}})\right| \\ =\frac{\left|3.2+1.(-1)\right|}{\sqrt{3^2+1^2}.\sqrt{2^2+{(-1)}^2}}=\frac{\sqrt{2}}{2} \\ \Rightarrow (d,d\text{'})={45}^o \end{gathered}$$

Bài 2: Tính góc giữa hai đường thẳng d: $\left\{\begin{array}{l}x=2+2t\\ y=1+3t\end{array}\right.$và d’: $\left\{\begin{array}{l}x=4+t\\ y=2+t\end{array}\right.$.

Lời giải:

Hai đường thẳng d và d’ có các vectơ chỉ phương lần lượt là: $\overrightarrow{u}=(2;3)$ và $\overrightarrow{u\text{'}}=(1;1)$. Ta có:

$$\begin{gathered} \cos (d,d\text{'})=\left|cos(\overrightarrow{u},\overrightarrow{u\text{'}})\right| \\ =\frac{\left|2.1+3.1\right|}{\sqrt{2^2+3^2}.\sqrt{1^2+1^2}}=\frac{5\sqrt{26}}{26} \\ \Rightarrow (d,d\text{'})\approx {11}^{o}18\text{'} \end{gathered}$$

Bài 3: Cho hai đường thẳng d và d’ có hệ số góc lần lượt là 3 và -1. Tính góc giữa d và d’.

Lời giải:

Ta có:

$$\begin{gathered} \tan (d,d\text{'})=\left|\frac{3-(-1)}{1+3.(-1)}\right|=2 \\ \Rightarrow (d,d\text{'})\approx {63}^{o}26\text{'} \end{gathered}$$

IV. Bài tập vận dụng

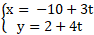
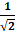
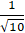
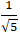
Bài 1: Tìm côsin góc giữa 2 đường thẳng d₁: và d₂:

A. B. C. D. tất cả sai

Lời giải:

Đáp án: D

Vectơ chỉ phương của d₁; d₂ lần lượt là u₁→(3; 4); u₂→(1; 1).

Cos( d₁; d₂) = |cos⁡(u₁→; u₂→) | =

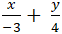
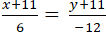
Bài 2: Góc giữa hai đường thẳng: (a): = 1 và (b): gần với số đo nào nhất?

A. 63⁰ B. 25⁰ C. 60⁰ D. 90⁰

Lời giải:

Đáp án: A

Đường thẳng (a) ⇔ 4x - 3y + 12 = 0 có VTPT n→( 4; -3).

Đường thẳng (b) có VTCP u→( 6; -12) nên VTPT n'→( 2; 1)

⇒ cos(a; b) =

⇒ Góc giữa hai đường thẳng đã cho xấp xỉ 63⁰.

Bài 3: Cho đường thẳng (a): x - y - 210 = 0 và đường thẳng (b): x + my + 47 = 0. Tìm m để góc giữa hai đường thẳng trên bằng 45⁰.

A. m = -1 B. m = 0 C. m = 1 D. m = 2

Lời giải:

Đáp án: B

Đường thẳng (a) có VTPT n→( 1; -1)

Đường thẳng (b) có VTPT n'→( 1; m)

Để góc giữa hai đường thẳng a và b bằng 45⁰ thì

Cos45⁰ =

⇔ |1 - m| =

⇔ 1- 2m + m² = 1 + m²

⇔ -2m = 0 ⇔ m = 0

Bài 4: Cho đường thẳng (a): y = -x + 30 và (b): y = 3x + 600. Tính tan của góc tạo bởi hai đường thẳng (a) và (b)?

A. 1 B. 2 C. 3 D. 4

Lời giải:

Đáp án: B

Gọi α là góc tạo bởi hai đường thẳng (a) và (b).

Đường thẳng (a) có hệ số góc k₁ = -1 và đường thẳng (b) có hệ số góc k₂ = 3.

⇒ Tan của góc tạo bởi hai đường thẳng trên là:

Tgα = 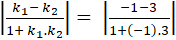= 2

Bài 5: Cho hai đường thẳng (d₁): y = -2x + 80 và (d₂) : x + y - 10 = 0. Tính tan của góc tạo bởi hai đường thẳng d₁ và d₂?

A. 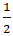B. 1 C. 3 D.

Lời giải:

Đáp án: D

Đường thẳng (d₁) có hệ số góc k₁ = - 2.

Đường thẳng (d₂) ⇔ y = -x + 10 có hệ số góc k₂ = -1.

⇒ tan của góc tạo bởi hai đường thẳng trên là:

tgα =

Bài 6: Cho đường thẳng (a): 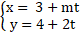và đường thẳng ( b): 2x + y - 40 = 0.Hỏi có bao nhiêu giá trị của m để góc giữa hai đường thẳng trên bằng 45⁰.

A. 1 B. 2 C. 3 D. 4

Lời giải:

Đáp án: B

+ Đường thẳng (a) có VTCP u→( m; 2) nên có VTPT n→( 2; -m) .

+ Đường thẳng (b) có VTPT n'→( 2;1).

+ Để góc giữa hai đường thẳng trên bằng 45⁰ thì:

Cos45⁰ =

⇔ .√5 = √2|4 - m|

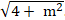
⇔ ( 4 + m²).5 = 2(16 - 8m + m²)

⇔ 20 + 5m² = 32 - 16m + 2m²

⇔ 3m2 + 16m - 12 = 0 ⇔ m = 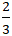hoặc m = - 6

Xem thêm tổng hợp công thức môn Toán lớp 10 đầy đủ và chi tiết khác:

Công thức viết phương trình đường thẳng theo đoạn chắn hay, chi tiết nhất

Công thức tìm điểm đối xứng qua đường thẳng hay và chi tiết

Công thức viết phương trình đường phân giác hay chi tiết nhất

Công thức về vị trí tương đối của hai đường thẳng hay và chi tiết nhất

Công thức tính khoảng cách từ một điểm đến một đường thẳng