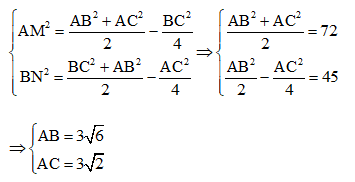Công thức tính độ dài đường trung tuyến (2024) chi tiết nhất
Với Công thức tính độ dài đường trung tuyến chi tiết nhất - Toán lớp 10 chi tiết nhất giúp học sinh dễ dàng nhớ toàn Công thức tính độ dài đường trung tuyến chi tiết nhất biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Công thức tính độ dài đường trung tuyến chi tiết nhất - Toán lớp 10
I. Lí thuyết tổng hợp.
- Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.
- Các đường trung tuyến của tam giác giao nhau tại trọng tâm của tam giác.
- Trong tam giác ABC cân tại A và M là trung điểm của BC thì đường trung tuyến AM cũng là đường cao, đường phân giác và đường trung trực.
- Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
- Độ dài đường trung tuyến: Gọi là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:
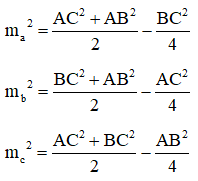
II. Các công thức.
Cho tam giác ABC vuông tại A, M là trung điểm của BC ta có: .
Gọi là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:
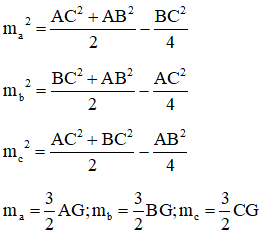
(với G là trọng tâm của tam giác ABC).
III. Ví dụ minh họa.
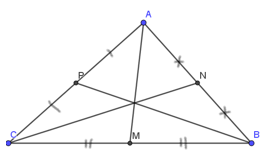
Bài 1: Cho tam giác ABC có AB = 5cm, AC = 4cm và BC = 4cm. Các điểm M, N, P lần lượt là là trung điểm của BC, AB, AC. Tính độ dài AM, BP và CN.
Lời giải:
Các điểm M, N, P lần lượt là là trung điểm của BC, AB, AC.
AM, BP, CN là các đường trung tuyến của tam giác ABC.
Xét tam giác ABC ta có:
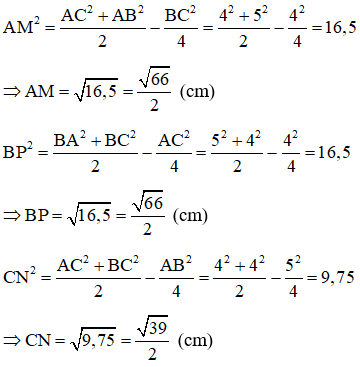
Bài 2: Cho tam giác ABC vuông tại A. Có BC = 10cm. Điểm M là trung điểm của BC. Tính độ dài AM.
Lời giải:
Xét tam giác ABC vuông tại A có:
M là trung điểm của BC AM là đường trung tuyến ứng với cạnh huyền BC.
(cm)
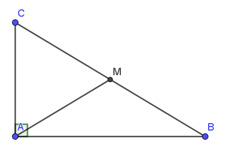
Bài 3: Cho tam giác ABC có trọng tâm G, N là trung điểm của AB. Tính độ dài CN biết CG = 4cm.
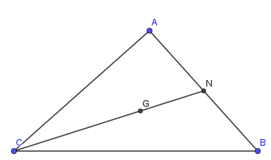
Lời giải:
Xét tam giác ABC có trọng tâm G ta có:
N là trung điểm BC CN là đường trung tuyến, điểm G nằm trên CN
Ta có:
(cm)
IV. Bài tập vận dụng
Bài 1. Tam giác ABC có AB = AC = 10 cm, BC = 12 cm. Tính độ dài đường trung tuyến AM.
Hướng dẫn giải:
Ta có tam giác ABC cân tại A, AM là trung tuyến suy ra AM là đường cao, đường phân giác của tam giác ABC nên BM = MC = BC = 6 cm
Áp dụng định lý Pythagore cho tam giác vuông AMC có:
AC2 = AM2 + MC2 = 8 cm
Bài 2. Tính độ dài đường trung tuyến AM của tam giác ABC có góc , AB = 4 cm, AC = 6 cm
Hướng dẫn giải:
Ta có BC2 = AB2 + AC2 - 2.AB.AC.cos120o
Bài 3. Cho tam giác ABC vuông tại A có độ dài hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm. Tính độ dài cạnh AB.
Hướng dẫn giải:
Tam giác ABC vuông tại A, AM là trung tuyến nên AM = BM = MC = 6
Suy ra BC = 12
Mặt khác:
Bài 4. Cho tam giác ABC cân ở A có AB = AC = 17 cm, BC= 16 cm. Kẻ trung tuyến AM.
a) Chứng minh: AM ⊥ BC;
b) Tính độ dài AM.
Hướng dẫn giải:
a. Ta có AM là đường trung tuyến tam giác ABC nên MB = MC
Mặt khác tam giác ABC là tam giác cân tại A
Suy ra AM vừa là đường trung tuyến vừa là đường cao
Vậy AM vuông góc với BC
b. Ta có
BC = 16cm nên BM = MC = 8cm
AB = AC = 17cm
Xét tam giác AMC vuông tại M
Áp dụng định lý Pythagore ta có: AC2 = AM2 + MC2 hay 172 = AM2 + 82.
Suy ra AM2 = 172 – 82 = 225.
Do đó AM = 15 cm.
Bài 5. Cho tam giác MNP cân ở M có MB = MC = 17 cm, NP= 16 cm. Kẻ trung tuyến MI.
a) Chứng minh: MI ⊥ NP;
b) Tính độ dài MI.
Hướng dẫn giải:
a) Do MI là đường trung tuyến MNP nên IP = IN.
Mặt khác tam giác MNP cân tại M.
Do đó MI vừa là đường trung tuyến vừa là đường cao hay MI ⊥ NP.
b) Ta có:
• NP = 16 cm nên NI = PI = 8 cm.
• MN = MP = 17 cm.
Xét tam giác MIP vuông tại I
Áp dụng định lý Pythagore, ta có:
• MP2 = MI2 + IP2 hay 192 = MI2 + 82
• MI2 = 172 – 82 = 225 suy ra MI = 15 cm.
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)