Nội dung bài viết

    Xem thêm

    Các công thức tính diện tích tam giác (2024) đầy đủ, chi tiết nhất

    Với Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất - Toán lớp 10 chi tiết nhất giúp học sinh dễ dàng nhớ toàn Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất biết cách làm bài tập Toán 10. Mời các bạn đón xem:

    1 23,638 12/03/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất - Toán lớp 10

    I. Các công thức

    Cho tam giác có BC = a, AC = b, AB = c với:

    • ha,  hb,  hc là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB

    • R là bán kính đường tròn ngoại tiếp tam giác;

    • r là bán kính đường tròn nội tiếp tam giác;

    • p=a+b+c2 là nửa chu vi tam giác;

    • S là diện tích tam giác.

    Khi đó ta có các công thức tính diện tích tam giác ABC như sau:

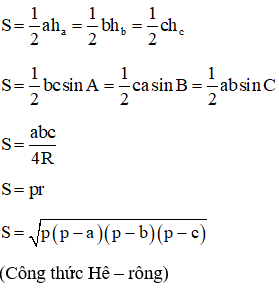
    Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất - Toán lớp 10 (ảnh 1)

    + Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.

    II. Ví dụ minh họa

    Bài 1. Cho tam giác ABC có AB = 3, AC = 6, BAC^=60°. Tính diện tích tam giác ABC.

    Lời giải:

    Diện tích tam giác ABC là:

    S=12AB.AC.sinBAC

    =12.3.6.sin60°=932(đvdt).

    Bài 2. Tam giác ABC có AC = 4, BAC^=30°, ACB^=75°. Tính diện tích tam giác ABC.

    Lời giải:

    Theo định lý tổng 3 góc trong tam giác ABC, ta có:

    Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất - Toán lớp 10 (ảnh 1)

    Bài 3. Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:

    Lời giải:

    Nửa chu vi tam giác ABC là:

    p=a+b+c2=21+17+102=24 (đvđd)

    Theo công thức Hê – rông, ta có diện tích tam giác ABC là:

    S=pp−ap−bp−c

    =2424−2124−1724−10=84 (đvdt).

    Bài 4. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng bao nhiêu?

    Lời giải:

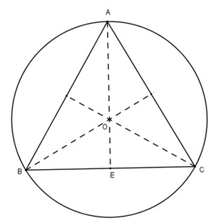
    Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất - Toán lớp 10 (ảnh 1)

    Giả sử tam giác thỏa mãn yêu cầu đề bài là tam giác ABC đều có cạnh a (cm, a > 0).

    Theo đề bài ta có, đường tròn có bán kính R = 4 cm là đường tròn ngoại tiếp tam giác ABC, khi đó tâm O của đường tròn chính là giao của ba đường trung trực của tam giác.

    Mà tam giác ABC đều nên O đồng thời là trực tâm của tam giác.

    Gọi E là trung điểm của BC

    Khi đó ta có: AE=32AO (tính chất trọng tâm)

    Mà AO = R = 4 cm

    Do đó: AE = 6 cm

    Tam giác ABC đều nên trung tuyến AE cũng là đường cao.

    Theo định lý Py – ta – go trong tam giác vuông ABE ta có:

    AB2=AE2+BE2

    Suy ra: a2=62+a22⇒a=43cm

    Vậy diện tích tam giác đều ABC là:

    S=AB.AC.BC4R=4334.4=123(cm2).

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 23,638 12/03/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: