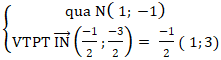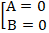Phương trình tiếp tuyến của đường tròn (lý thuyết, công thức và cách giải các dạng bài tập)
Với tài liệu về Phương trình tiếp tuyến của đường tròn bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Toán hơn.
Phương trình tiếp tuyến của đường tròn
I. Lý thuyết Phương trình tiếp tuyến của đường tròn
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính tại điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
- Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
- Từ một điểm trên đường tròn ta có duy nhất một tiếp tuyến đi qua điểm đó. Từ một điểm ngoài đường tròn, ta có hai tiếp tuyến với đường tròn đi qua điểm đó.
II. Viết phương trình tiếp tuyến của đường tròn
Dạng 1. Viết phương trình tiếp tuyến của đường tròn tại một điểm thuộc đường tròn
- Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm M(x0;y0) thuộc đường tròn (C).
+ Nếu phương trình đường tròn có dạng x2+y2−2ax−2by+c=0 thì phương trình tiếp tuyến là: xx0+yy0−a(x+x0)−b(y+y0)+c=0.
+ Nếu phương trình đường tròn có dạng (x−a)2+(y−b)2=R2 thì phương trình tiếp tuyến là: (x−a)(x0−a)+(y−b)(y0−b)=R2
Dạng 2. Viết phương trình tiếp tuyến của đường tròn tại một điểm ngoài đường tròn
- Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm N(x0;y0) nằm ngoài đường tròn (C).
+ Viết phương trình của đường thẳng đi qua điểm N:
y−y0=m(x−x0)⇔mx−y−mx0+y0=0 (1)
+ Có d(I,d)=R ta tính được m thay m vào phương trình (1) ta được phương trình tiếp tuyến. Ta luôn tìm được hai đường tiếp tuyến.
Dạng 3. Viết phương trình tiếp tuyến song song với phương cho sẵn có hệ số góc k
Phương trình đường thẳng (d) có dạng y = kx + m (m chưa biết)
kx - y + m = 0
Cho khoảng cách từ tâm I đến (d) = R ta tìm được m
Ta luôn tìm được 2 tiếp tuyến
III. Ví dụ minh họa
Bài 1: Cho đường tròn (C): (x−1)2+y2=18. Viết phương trình tiếp tuyến của (C) tại điểm A(-2; 3).
Lời giải:
Phương trình tiếp tuyến của (C) tại điểm A(-2; 3) là:
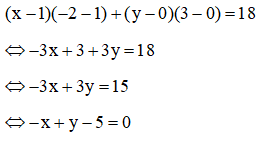
Bài 2: Cho đường tròn (C): (x−1)2+(y−1)2=5. Viết phương trình tiếp tuyến của (C) tại điểm B(-1; 2).
Lời giải:
Phương trình tiếp tuyến của (C) là:
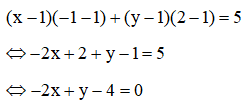
Bài 3: Cho đường tròn (C): (x−4)2+(y+3)2=2. Viết phương trình tiếp tuyến của (C) đi qua điểm C(4; 0).
Lời giải:
Gọi tiếp tuyến của (C) cần tìm là đường thẳng d
Ta có điểm C không thuộc đường tròn (C)
Phương trình đường thẳng đi qua điểm C là:
y−0=m(x−4)⇔mx−4m−y=0
Tâm của đường tròn (C) là I(4; -3) và bán kính R=√2
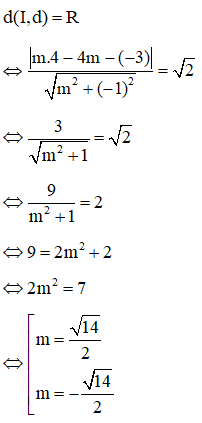
Với m=−√142, có phương trình tiếp tuyến là: √142x−4.√142−y=0
⇔√142x−y−2√14=0
Với m=−√142, có phương trình tiếp tuyến là: −√142x−4.(−√142)−y=0
⇔−√142x−y+2√14=0
IV. Bài tập vận dụng
Câu 1: Phương trình tiếp tuyến d của đường tròn (C): x2 + y2 - 3x-y= 0 tại điểm N(1;-1) là:
A. d: x + 3y - 2 = 0 B. d: x - 3y + 4 = 0
C. d: x - 3y - 4 = 0 D. d: x + 3y + 2 = 0
Đáp án: D
Trả lời:
+ Đường tròn (C) có tâm I( 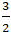
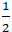
+ Do đường thẳng d tiếp xúc với đường tròn ( C) tại điểm N nên đường thẳng d vuông góc với đường thẳng IN.
+ Phương trình đường thẳng (d) :
⇒(d): 1(x - 1) + 3( y + 1) = 0 hay ( d): x + 3y + 2 = 0
Câu 2: Cho đường tròn( C): x2 + y2 - 2x + 8y - 23 = 0 và điểm M( 8; -3) . Độ dài đoạn tiếp tuyến của ( C) xuất phát từ M là :
A. 10 B. 2√10 C. 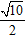
Đáp án: D
Trả lời:
Đường tròn ( C) có tâm I( 1; -4) bán kính R = √40 .
Độ dài IM = 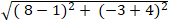
⇒ Điểm M nằm ngoài đường tròn. Khi đó từ M sẽ kẻ được hai tiếp tuyến là MA và MB- trong đó A và B là hai tiếp điểm .
Theo tính chất hai tiếp tuyến cắt nhau ta có:
MA = MB = 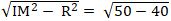
Vậy độ dài tiếp tuyến là : √10.
Câu 3: Cho đường tròn ( C ) : x2 + y2 - 3x - y = 0. Phương trình tiếp tuyến của ( C) tại M(1 ; -1) là:
A. x + 3y - 1 = 0 B. 2x - 3y + 1 = 0
C. 2x - y + 4 = 0 D. x + 3y + 2 = 0
Đáp án: D
Trả lời:
Đường tròn ( C) có tâm I( 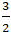
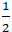
Điểm M(1; -1) thuộc đường tròn ( C).
Phương trình tiếp tuyến của đường tròn ( C) tại điểm M là đường thẳng đi qua M và nhận vec tơ IM→ = (- 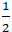
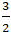
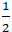
1( x - 1) + 3( y + 1) = 0 hay x + 3y + 2 = 0
Câu 4: Cho đường tròn (x - 3)2 + (y - 1)2 = 10. Phương trình tiếp tuyến của ( C) tại điểm A( 4; 4) là
A. x - 3y + 5 = 0 B. x + 3y - 4 = 0
C. x - 3y + 16 = 0 D. x + 3y - 16 = 0
Đáp án: D
Trả lời:
Đường tròn ( C) có tâm I(3; 1) và bán kính R = √10.
Tiếp tuyến của ( C) tại A là đường thẳng qua A( 4; 4) và nhận vecto IA→( 1; 3) là vectơ pháp tuyến của tiếp tuyến d.
Suy ra (d) : 1( x - 4) + 3( y - 4) = 0 hay x + 3y - 16 = 0
Câu 5: Cho đường tròn (x - 2)2 + (y - 2)2 = 9 . Phương trình tiếp tuyến của (C) đi qua điểm A( 5; -1) là
A. x + y - 4 = 0 và x - y - 2 = 0 .
B. x = 5 và y = -1.
C. 2x - y - 3 = 0 và 3x + 2y - 3 = 0.
D. 3x - 2y + 1 = 0 và 2x + 3y + 5 = 0
Đáp án: B
Trả lời:
+ Đường tròn (C) có tâm I( 2; 2) và bán kính R = 3.
+ ∆ là tiếp tuyến cần tìm : đi qua A(5, -1) và nhận VTPT n→( A; B)
⇒ (∆ ) : A( x - 5) + B( y + 1) = 0 (*)
+ Do ∆ là tiếp tuyến của ( C) nên :
d( I ; ∆) = R ⇔ 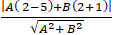
⇔ |-3A + 3B| = 3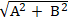
⇔ 18AB = 0 ⇔
+ Với A =0 ; chọn B = 1 thay vào (*) ta được : y + 1 = 0
+ Với B = 0 ; chọn A = 1 thay vào ( *) ta được :x - 5 = 0
Vậy có hai tiếp tuyến thỏa mãn là y + 1 = 0 và x - 5 = 0
Câu 6: Cho đường tròn (C): x2 + y2 + 2x - 6y + 5 = 0 . Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y - 15 = 0 là
A. x + 2y = 0 và x + 2y - 10 = 0.
B. x - 2y = 0 và x - 2y + 10 = 0.
C. x + 2y - 12 = 0 và x + 2y + 22 = 0
D. x + 2y + 3 = 0 và x + 2y + 7 = 0
Đáp án: A
Trả lời:
+ Đường tròn ( C) có tâm I( -1;3) và bán kính R = 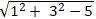
+ Do tiếp tuyến cần tìm song song với đường thẳng d: x + 2y- 15= 0 nên tiếp tuyến ∆ có dạng : x + 2y + m= 0 ( m≠-15) .
+ ∆ là tiếp tuyến của ( C) khi và chỉ khi:
d(I ;∆) = R ⇔ 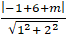
⇔
⇒ Có hai tiếp tuyến thỏa mãn là : x + 2y = 0 và x + 2y - 10 = 0
Câu 7: Cho đường tròn (C): (x−2)2+(y−3)2=16. Viết phương trình tiếp tuyến của (C) tại điểm B(2; 7).
Câu 8: Cho đường tròn (C): (x−4)2+(y+3)2=25. Viết phương trình tiếp tuyến của (C) đi qua điểm C(2; 3).
Xem thêm tổng hợp công thức môn Toán lớp 10 đầy đủ và chi tiết khác:
Công thức xác định khoảng cách giữa hai đường thẳng song song
Công thức xác định tâm và bán kính của đường tròn hay, chi tiết nhất
Công thức viết phương trình đường tròn
Công thức xác định tiêu điểm, tiêu cự, tâm sai, độ dài trục lớn, trục bé của Elip
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)