Công thức lượng giác (2024) và cách giải bài tập chi tiết nhất
Với các bài toán về Công thức lượng giác chi tiết và cách giải bài tập Toán lớp 10 Đại số gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập Công thức lượng giác chi tiết và cách giải bài tập lớp 10. Mời các bạn đón xem:
Công thức lượng giác chi tiết và cách giải bài tập
I. Tổng hợp các công thức lượng giác
1. Công thức cộng lượng giác
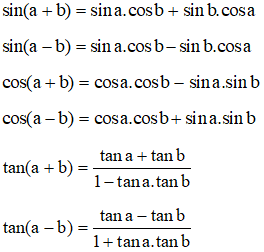
2. Công thức nhân, hạ bậc lượng giác
* Công thức nhân đôi:
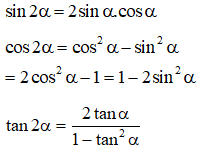
* Công thức hạ bậc:
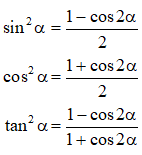
* Công thức nhân ba:
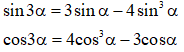
3. Công thức biến đổi tích thành tổng
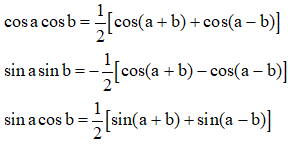
4. Công thức biển đổi tổng thành tích

5. Công thức nghiệm của phương trình lượng giác
a) Phương trình lượng giác cơ bản
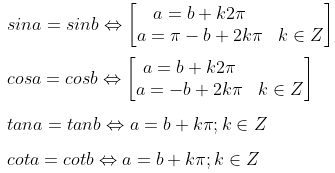
b) Phương trình lượng giác đặc biệt
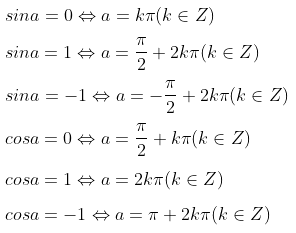
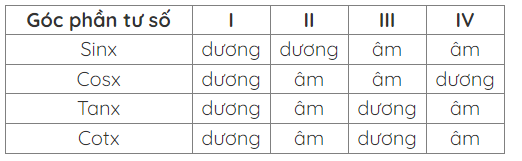
6. Bảng xét dấu của các giá trị lượng giác
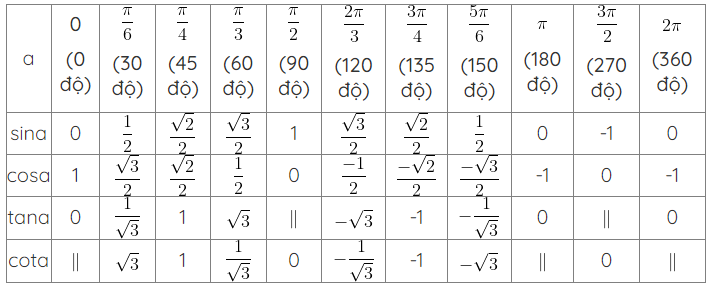
7. Bảng giá trị lương giác của các góc đặc biệt
II. Các dạng bài tập lượng giác
Dạng 3.1: Tính giá trị lượng giác của góc đặc biệt
a. Phương pháp giải:
- Sử dụng định nghĩa giá trị lượng giá của một góc.
- Sử dụng tính chất và bảng giá trị lượng giác đặc biệt.
- Sử dụng các công thức lượng giác.
b. Ví dụ minh họa
Ví dụ 1: Tính:
a. ;
b. .
Hướng dẫn:
a.
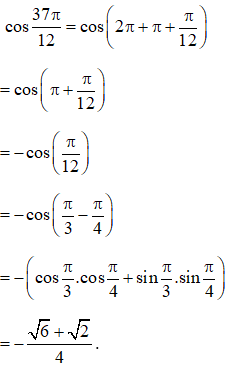
b.
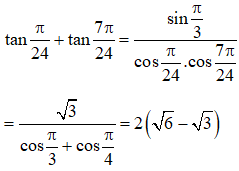
Ví dụ 2: Tính:
a. biết với ;
b. biết , và , .
Hướng dẫn:
a. Ta có:
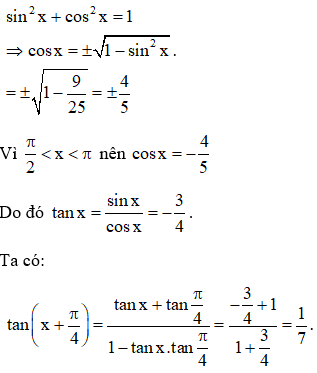
b. Ta có:
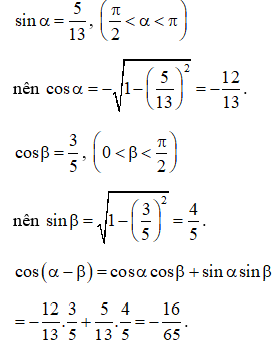
Dạng 3.2: Chứng minh đẳng thức lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Dùng hệ thức lượng giác biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
b. Ví dụ minh họa:
Ví dụ 1: Chứng minh rằng:
a.
b.
Hướng dẫn:
a. (Áp dụng công thức hạ bậc) Ta có:
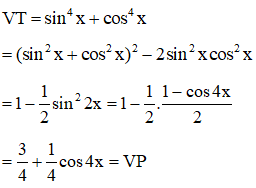
Suy ra đpcm.
b. (Áp dụng công thức góc nhân ba) Ta có:
Suy ra đpcm.
Ví dụ 2: Cho tam giác ABC. Chứng minh rằng:
Hướng dẫn:
Do tam giác ABC có , suy ra
Do đó, ta có:
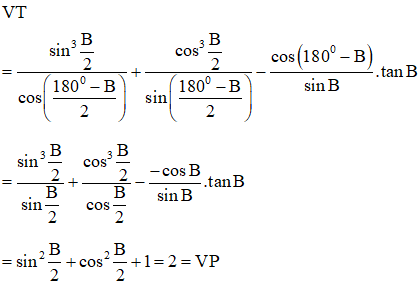
Suy ra đpcm.
Dạng 3.3: Thu gọn biểu thức lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
b. Ví dụ minh họa:
Ví dụ 1: Rút gọn biểu thức:
a.
b.
Hướng dẫn:
a. Ta có:
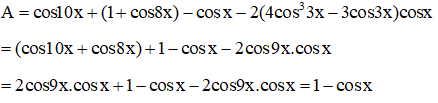
b. Ta có:
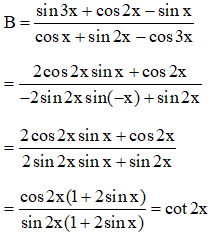
Ví dụ 2: Rút gọn biểu thức:
Hướng dẫn:
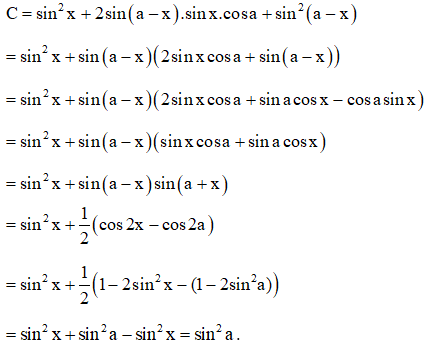
Dạng 3.4: Chứng minh biểu thức không phụ thuộc vào biến
a. Phương pháp giải:
Chứng minh biểu thức không phụ thuộc vào biến tức là sau khi rút gọn biểu thức ta được kết quả không chứa biến. Do đó, để giải dạng toán này, ta sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn. Nếu biểu thức sau khi thu gọn không chứa biến, ta suy ra điều phải chứng minh.
b. Ví dụ minh họa:
Ví dụ 1: Chứng minh biểu thức sau không phụ thuộc vào x:
Hướng dẫn:
Ta có:
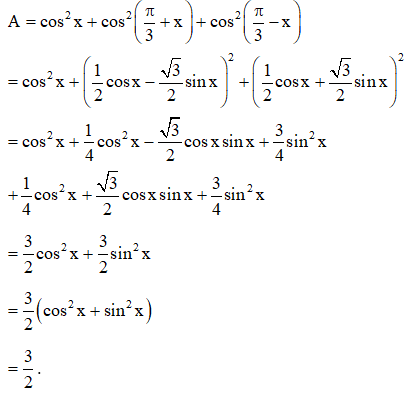
Vậy biểu thức đã cho không phụ thuộc vào x.
Ví dụ 2: Chứng minh biểu thức sau không phụ thuộc vào x:
Hướng dẫn:
Ta có:
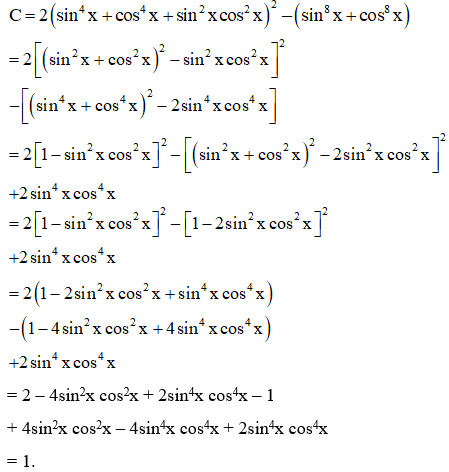
Vậy biểu thức đã cho không phụ thuộc vào x.
Dạng 3.5: Tính giá trị biểu thức
a. Phương pháp giải:
Sử dụng hệ thức cơ bản, các công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt.
b. Ví dụ minh họa:
Ví dụ 1: Tính giá trị biểu thức: .
Hướng dẫn:
Ta có:
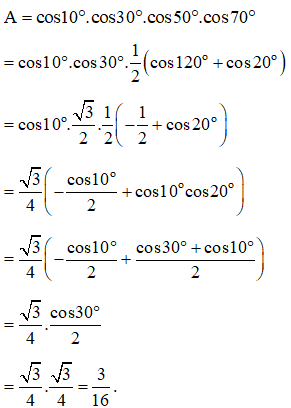
Ví dụ 2: Cho . Tính giá trị của biểu thức .
Hướng dẫn:
Ta có:
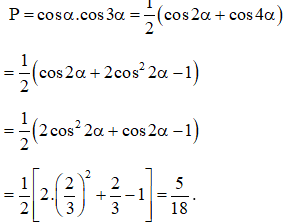
III. Bài tập vận dụng
a. Tự luận
Câu 1: Cho , chứng minh rằng: tanx + tany + tanz = tanx . tany . tanz.
Hướng dẫn:
Từ giả thiết, ta có:
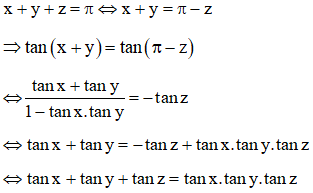
Suy ra đpcm.
Câu 2: Cho , với . Chứng minh rằng: .
Hướng dẫn:
Từ giả thiết, ta có:
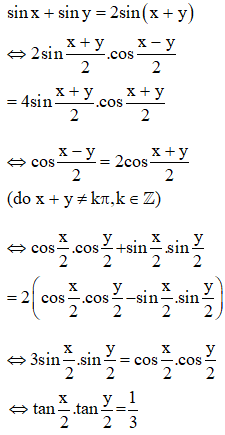
Suy ra đpcm.
Câu 3: Cho với . Tính giá trị của .
Hướng dẫn:
Ta có:
(vì nên ).
Ta có:
Câu 4: Tính giá trị biểu thức .
Hướng dẫn:
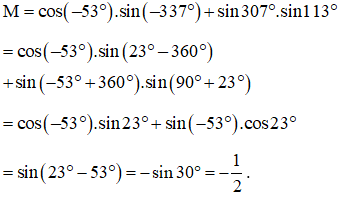
Câu 5: Cho số thực thỏa mãn . Tính .
Hướng dẫn:
Ta có:
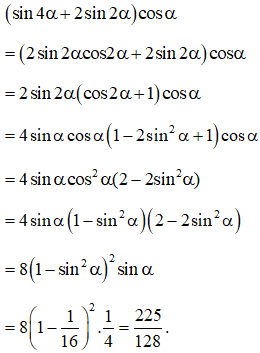
Câu 6: Rút gọn biểu thức .
Hướng dẫn:
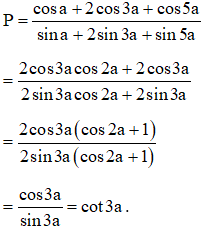
Câu 7: Chứng minh biểu thức không phụ thuộc vào x.
Hướng dẫn:
Ta có:
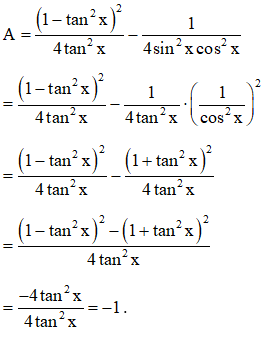
Vậy biểu thức không phụ thuộc vào biến.
Câu 8: Rút gọn biểu thức .
Hướng dẫn:
Ta có:
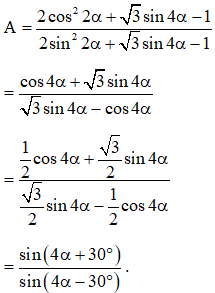
Câu 9: Biến đổi biểu thức thành tích các biểu thức.
Hướng dẫn:
Ta có:
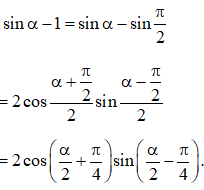
Câu 10: Biết , và . Chứng minh biểu thức: không phụ thuộc vào .
Hướng dẫn:
Ta có
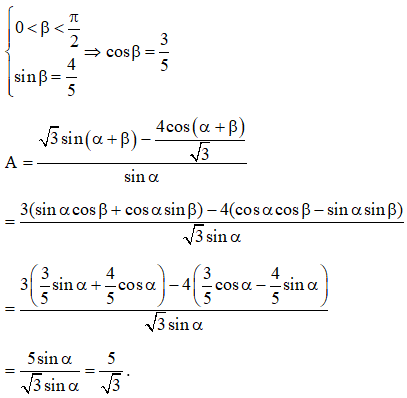
Vậy biểu thức không phụ thuộc vào biến α.
b. Trắc nghiệm
Câu 1: Kết quả nào sau đây sai?
A. .
B. .
C. .
D. .
Câu 2: Trong các công thức sau, công thức nào sai?
A. .
B. .
C. .
D.
Câu 3: Nếu thì sin2x bằng
A. .
B. .
C. .
D. .
Câu 4: Cho hai góc nhọn a và b. Biết , . Giá trị bằng:
A.
B.
C.
D.
Câu 5: Cho . Tính .
A. .
B. 2.
C. 1.
D. .
Đáp án:

Xem thêm các dạng bài tập Toán lớp 10 có đáp án và lời giải chi tiết khác:
Góc và cung lượng giác và cách giải bài tập
Giá trị lượng giác của cung và cách giải bài tập
Các định nghĩa về vectơ và cách giải bài tập
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)
