Các định nghĩa về vectơ và cách giải bài tập (2024) chi tiết nhất
Với các bài toán về Các định nghĩa về vectơ và cách giải bài tập Toán lớp 10 Hình học gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập Các định nghĩa về vectơ và cách giải bài tập lớp 10. Mời các bạn đón xem:
Các định nghĩa về vectơ và cách giải bài tập – Toán lớp 10
A. Lí thuyết.
- Vectơ là đoạn thẳng có hướng. Kí hiệu vectơ có điểm đầu A và điểm cuối B được kí hiệu là →AB.
- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ .
- Độ dài vectơ là khoảng cách giữa điểm đầu và điểm cuối của. Độ dài vectơ →AB có kí hiệu |→AB|.
- Vectơ - không là một vectơ có điểm đầu trùng với điểm cuối. Kí hiệu là →0.
- Hai vectơ cùng phương là hai vec tơ có giá song song hoặc trùng nhau. Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngước hướng.
- Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
- Hai vectơ đối nhau nếu chúng ngược hướng và cùng độ dài.
- Chú ý:
+ Vectơ - không cùng hướng với mọi vectơ.
+ Mọi vectơ →0 đều bằng nhau và có độ dài bằng 0.
+ Vectơ còn được kí hiệu là: →u,→x,→y,→z,...
B. Phương pháp giải.
Nắm chắc các định nghĩa về vectơ: Định nghĩa vectơ, kí hiệu, giá của vectơ, hai vectơ cùng phương (cùng hướng, ngược hướng), độ dài vectơ, hai vectơ bằng nhau, hai vectơ đối nhau, vectơ – không.
C. Ví dụ minh họa.
Bài 1: Cho hình bình hành ABCD. Liệt kê các cặp vecto cùng hướng và ngược hướng trong hình bình hành ABCD.
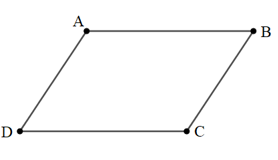
Giải:
Do ABCD là hình bình hành nên ta có: AB // DC và AD // BC.
Các cặp vectơ cùng hướng: →AB và →DC, →AD và →BC, →BA và →CD, →DA và →CB.
Các cặp vectơ ngược hướng: →AB và →CD, →AD và →CB , →BA và →DC, →DA và →BC.
Bài 2: Cho tam giác ABC vuông tại A. Có AB = AC = a. Biết I là trung điểm của BC. Từ I vẽ IH vuông góc với AB, vẽ IK vuông góc với AC. Chứng minh rằng: →IH=→KA.
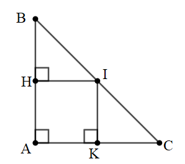
Giải:
Xét tam giác ABC vuông tại A.
+) Ta có: IH ⊥ AB tại H và AC ⊥ AB tại A.⇒ IH // AC. (1)
Áp dụng định lý Ta-lét ta có:
IHAC=BIBC=12⇒IH=12AC=a2 (2)
+) Ta có: IK ⊥ AC tại K và AB ⊥ AC tại A. ⇒ IK // AB.
Áp dụng định lí Ta-lét ta có:
AKAC=BIBC=12⇒AK=12AC=a2 (3)
+) Từ (2) và (3) ta có: IH = AK (4)
+) Từ (4) và (1) ta có: →IH=→KA (điều cần phải chứng minh)
Bài 3: Cho hình chữ nhật ABCD. M là trung điểm của AB. Biết AB = 2a, AD = a. Tính độ dài vectơ →MD,→BD.
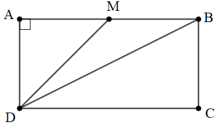
Giải:
+) Có M là trung điểm của AB ⇒MA=12AB=12.2a=a
+) Xét tam giác ADM vuông tại A.
Áp dụng định lý Py-ta-go ta có:
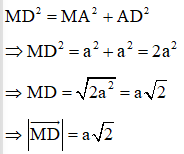
+) Xét tam giác ADB vuông tại A.
Áp dụng định lý Py-ta-go ta có:
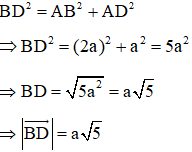
D. Bài tập tự luyện.
Bài 1: Cho 2 vectơ →x và →y. Mệnh đề nào sau đây là đúng ?
A. Nếu 2 vectơ →x và →y cùng phương thì 2 vectơ →x và →y cùng hướng.
B. Nếu 2 vectơ →x và →y cùng hướng thì 2 vectơ →x và →y cùng phương.
C. Nếu 2 vectơ →x và →y bằng nhau thì 2 vectơ →x và →y ngược hướng.
D. Nếu 2 vectơ →x và →y đối nhau thì 2 vectơ →x và →y cùng hướng.
Đáp án: B
Bài 2: Nhận định nào sau đây là đúng về vectơ ?
A. Vectơ chỉ là một đoạn thẳng không có hướng.
B. Vectơ là một đường thẳng.
C. Vectơ là đoạn thẳng có hướng, điểm đầu và điểm cuối được xác định rõ.
D. Điểm đầu điểm cuối của vectơ thay đổi thì vectơ không đổi.
Đáp án: C
Bài 3: Nhận định nào sau đây là đúng về độ dài của vectơ ?
A. Độ dài vectơ là độ dài đoạn thẳng tạo thành vectơ.
B. Độ dài vectơ - không là rất lớn.
C. Tất cả vectơ đều không xác định được độ dài.
D. Độ dài vectơ →CD được kí hiệu là CD.
Đáp án: A
Bài 4: Vectơ nào sau đây là vectơ – không ?
A. →AB ( A và B phân biệt )
B. →CB (C và B phân biệt )
C. →MN (M và N phân biệt )
D. →PP
Đáp án: D
Bài 5: Cho tam giác ABC vuông tại A. Có AH là đường cao. Biết AB = AC = 2a. Tính độ dài vectơ →AH.
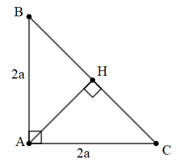
Đáp án: |→AH|=a√2
Bài 6: Cho điểm A và B phân biệt cùng nằm trên một đường thẳng. Điểm A cách điểm B nhau 10 đơn vị độ dài. Biết trung điểm của AB là I. Tính độ dài vectơ →AB và →AI.
Đáp án: |→AB|=10;|→AI|=5
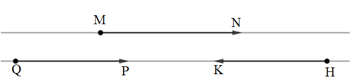
Bài 7: Cho vectơ →MN như hình vẽ. Hãy vẽ một vectơ →QP cùng hướng với vectơ →MN và một vectơ →HK ngược hướng với vectơ →MN.
![]()
Đáp án:
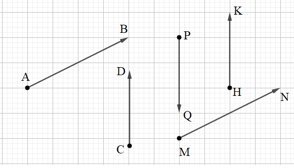
Bài 8: Cho hình vẽ sau. Hãy liệt kê các cặp vectơ cùng hướng và các cặp vectơ ngược hướng.

Đáp án:
Cùng hướng:→x và →a; →c và →z.
Ngược hướng: →y và →b.
Bài 9: Cho các đoạn thẳng AB = 9 , CD = 7 , MN = 9 , PQ = 7 , HK = 7 và hình vẽ như sau. Các vectơ nào bằng nhau ?
Đáp án: →AB=→MN;→CD=→HK
Bài 10: Cho hình vuông ABCD cạnh a. Gọi M là trung điểm của AB, N là điểm đối xứng với C qua D. Hãy tính độ dài các vectơ →MD,→MN.
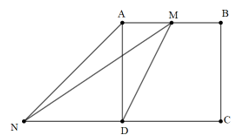
Đáp án: |→MD|=√52a;|→MN|=√132a
Xem thêm các dạng bài tập Toán lớp 10 có đáp án và lời giải chi tiết khác:
Tổng và hiệu của hai vectơ và cách giải bài tập
Tích của vectơ với một số và cách giải bài tập
Cách Phân tích vectơ và phương pháp giải bài tập
Tọa độ của vectơ, tọa độ của một điểm và cách giải bài tập
Giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)
