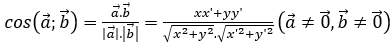Công thức tính góc giữa hai vectơ (2024) chi tiết nhất

Công thức góc giữa hai vectơ chi tiết nhất - Toán lớp 10

I. Lý thuyết góc giữa hai vecto

1. Góc giữa hai vecto là gì?

- Định nghĩa: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$. Từ một điểm O bất kì, ta vẽ hai vectơ $\overrightarrow{OA}=\overrightarrow{a}$ và $\overrightarrow{OB}=\overrightarrow{b}$. Khi đó, góc $\widehat{AOB}$ với số đo từ $0^o$ đến ${180}^o$ được gọi là góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

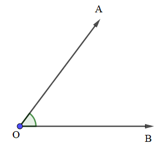
- Kí hiệu góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$: $(\overrightarrow{a},\overrightarrow{b})$

- Chú ý: Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$.

+ Nếu $(\overrightarrow{a},\overrightarrow{b})$ = ${90}^o\iff \overrightarrow{a}\perp \overrightarrow{b}$ hoặc $\overrightarrow{b}\perp \overrightarrow{a}$, $\overrightarrow{a}.\overrightarrow{b}=0$

+ Nếu $(\overrightarrow{a},\overrightarrow{b})$ = $0^o\iff$ Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng.

+ Nếu $(\overrightarrow{a},\overrightarrow{b})$ = ${180}^o\iff$ Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ ngược hướng.

2. Đặc điểm của góc giữa hai vecto

$(\overrightarrow{a},\overrightarrow{b}) = (\overrightarrow{b},\overrightarrow{a})$

- Góc giữa hai vecto cùng hướng và khác 0 luôn bằng 0^o

- Góc gữa hai vecto ngược hướng và khác $\overrightarrow{0}$ luôn bằng 180^o

- Nếu $(\overrightarrow{u},\overrightarrow{v})$ = 90^o thì ta nói $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau, kí hiệu là $\overrightarrow{u} \perp \overrightarrow{v}$ hoặc $\overrightarrow{v}\perp \overrightarrow{u}$. Đặc biệt $\overrightarrow{0}$ được coi là vuông góc với mọi vecto.

3. Định lí góc giữa hai vecto

- Góc không xác định nếu tồn tại 1 vecto không hay có thể nói góc bằng 0

- Cả hai vecto đều khác 0, tiến hành đưa về chung gốc để có thể tính toán.

II. Công thức tính góc giữa hai vecto

- Cho hai vectơ $\overrightarrow{OA}=\overrightarrow{a}$ và $\overrightarrow{OB}=\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$ ta có:

$(\overrightarrow{a},\overrightarrow{b})=\widehat{AOB}$ ($0^o\le \widehat{AOB}\le {180}^o$ )

- Cho hai vectơ $\overrightarrow{a}=(a_1;a_2)$ và $\overrightarrow{b}=(b_1;b_2)$ đều khác vectơ $\overrightarrow{0}$ ta có:

$$\begin{gathered} \cos (\overrightarrow{a},\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1+a_2}.\sqrt{b_1+b_2}} \\ \overrightarrow{a}\perp \overrightarrow{b}\iff (\overrightarrow{a},\overrightarrow{b})={90}^o \\ \iff \overrightarrow{a}.\overrightarrow{b}=0 \\ \iff a_1.b_1+a_2.b_2=0 \end{gathered}$$

- Lưu ý: Góc giữa hai vectơ luôn có số đo từ $0^o$ đến ${180}^o$.

III. Cách tính góc giữa hai vecto

Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ

Định nghĩa góc giữa hai vectơ: Cho hai vectơ đều khác vectơ-không. Từ một điểm O bất kỳ, ta vẽ các vectơ . Khi đó số đo của góc AOB, được gọi là số đo góc giữa hai vectơ , hoặc đơn giản là góc giữa hai vectơ .

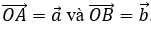
Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ

Sử dụng công thức sau:

Cho hai vectơ 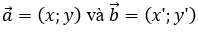. Khi đó

Chú ý: Góc giữa hai vectơ thuộc [0°;180°]

Ví dụ minh họa

VD 1: Cho hình thoi ABCD biết $\widehat{BAD}={120}^o$. Tính góc giữa hai vectơ $\overrightarrow{DC}$ và $\overrightarrow{AD}$.

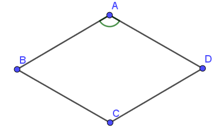
Lời giải:

Ta có: AB // DC và AB = DC (vì ABCD là hình thoi) $\Rightarrow \overrightarrow{AB}=\overrightarrow{DC}$

$\Rightarrow (\overrightarrow{DC},\overrightarrow{AD})=(\overrightarrow{AB},\overrightarrow{AD})$

Mà $(\overrightarrow{AB},\overrightarrow{AD})=\widehat{BAD}={120}^o$

$\Rightarrow (\overrightarrow{DC},\overrightarrow{AD})={120}^o$

VD 2: Cho các vectơ $\overrightarrow{a}=(1;2)$,$\overrightarrow{b}=(-2;5)$ và $\overrightarrow{c}=(-6;3)$. Tính góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{c}$.

Lời giải:

Ta có:

VD 3: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ có độ dài lần lượt là 6 và 8, tích vô hướng $\overrightarrow{a}.\overrightarrow{b}$ = 24. Tính góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

Lời giải:

Ta có: $\overrightarrow{a}.\overrightarrow{b}=24$, $\left|\overrightarrow{a}\right|=6$ và $\left|\overrightarrow{b}\right|=8$

$\cos (\overrightarrow{a},\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{24}{6.8}=\frac{1}{2}$

Góc giữa hai vectơ có số đo từ $0^o$ đến ${180}^o$ $\Rightarrow (\overrightarrow{a},\overrightarrow{b})={60}^o$.

IV. Bài tập vận dụng

Bài 1. Tính góc giữa vecto a và vectơ c, biết vectơ $\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}$ và cho các vectơ a và b thoả mãn |a| = 4, |b| = 2.

Hướng dẫn giải

Ta có: c = a – b

Nên c² = (a – b)² = a² – 2ab + b² = |a|² – 2|a| . |b| . cos(a,b) + |b|²

Suy ra c² = 4² – 2.4.1.cos60^o + 2² = 3 hay |c| = $\sqrt{3}$.

Ta lại có: a . c = a . (a – b) = a² – a . b hay a . c =3

Do đó a . c = |a| . |c| . cos (a, c)

Hay 3 = 2.$\sqrt{3}$. cos(a, c)

Do đó, cos(a, c) = $\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2}$

Vậy góc giữa 2 vectơ bằng 30^o.

Bài 2. Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là 1. Gọi M là trung điểm của canh AB. Tính góc giữa hai vectơ $\overrightarrow{OM},\overrightarrow{BC}$.

Hướng dẫn giải

Lấy N là trung điểm của AC suy ra MN // BC.

Ta có: $\left(\overrightarrow{OM},\overrightarrow{BC}\right)=\left(\overrightarrow{OM},\overrightarrow{MN}\right)=180°-\widehat{OMN}$

Xét tam giác OMN có OM = ON = $\frac{1}{\sqrt{2}}$; MN = $\frac{1}{2}$BC = $\frac{\sqrt{2}}{2}$

Suy ra $\cos \widehat{OMN}=\frac{1}{2}$ hoặc $\widehat{OMN}=60°$.

Do đó $\left(\overrightarrow{OM},\overrightarrow{BC}\right)=120°$.

Bài 3. Tính góc giữa 2 vectơ a và b, biết rằng 2 vectơ a và b có độ bài bằng 1 và thoả mãn điều kiện |3a + 2b| = $\sqrt{7}$.

Hướng dẫn giải

Ta có: $\left|3a+2b\right|=\sqrt{7}$ hay ${\left(3a\cdot 2b\right)}^2 =7$ nên 9a² + 12b + 4b = 7

Vì a² = |a|² =1; b² = |b|² =1.

Nê 4 . 1 + 12ab + 9 . 1 = 7 nên 12ab = 7 – 4 – 9 = –6 hay ab = $-\frac{1}{2}$.

Do đó: $cos\left(a;b\right)=\frac{a.b}{\left|a\right|.\left|b\right|}=-\frac{1}{2}$.

Vậy góc giữa 2 vectơ a và b là 120 độ.

Bài 4. Cho hình thoi ABCD có $\widehat{BAD}=120°$. Tính góc giữa hai vectơ $\overrightarrow{DC}$ và $\overrightarrow{AD}$.

Hướng dẫn giải

Ta có AB // DC và AB = DC (vì ABCD là hình thoi)

Suy ra $\overrightarrow{DC}=\overrightarrow{AD}$ nên $\left(\overrightarrow{DC},\overrightarrow{AD}\right)=\left(\overrightarrow{AB},\overrightarrow{AD}\right)$.

Mà $\left(\overrightarrow{AB},\overrightarrow{AD}\right)=\widehat{BAD}=120°$.

Do đó $\left(\overrightarrow{DC},\overrightarrow{AD}\right)=120°$.

Bài 5. Cho tứ diện ABCD có AC = BD = 2a. Gọi M, N lần lượt là trung điểm BC, AD. Biết rằng MN = $a\sqrt{3}$. Tính góc giữa AC và BD.

Hướng dẫn giải

Gọi I là trung điểm của AB, ta có IM = IN = a

Áp dụng định lý của Cosin cho tam giác IMN ta có:

$\cos \widehat{MIN}=\frac{I{M}^2+I{N}^2-M{N}^2}{2.IM.IN}$ = $\frac{a^2+a^2-3a^2}{2.a.a}=-\frac{1}{2}$

=> $\widehat{MIN}=60°$.

Vậy góc giữa AC và BD bằng 60 độ.