Công thức tính độ dài vectơ (2024) chi tiết nhất

Với Công thức tính độ dài vectơ chi tiết nhất - Toán lớp 10 chi tiết nhất giúp học sinh dễ dàng nhớ toàn Công thức tính độ dài vectơ chi tiết nhất biết cách làm bài tập Toán 10. Mời các bạn đón xem:

1 26,380 17/07/2024

Trang trước

Trang sau

Công thức tính độ dài vectơ chi tiết nhất - Toán lớp 10

I. Lí thuyết tổng hợp.

- Định nghĩa: Mỗi vecto đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vectơ $\vec{A B}$ chính bằng độ dài đoạn thẳng AB. Kí hiệu: $|\vec{A B}|$

- Độ dài của vectơ $\vec{a} = (a_{1}; a_{2})$ được tính theo công thức: $|\vec{a}| = \sqrt{{a_{1}}^{2} + {a_{2}}^{2}}$ .

II. Các công thức.

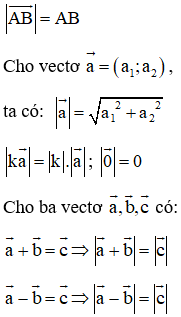
Công thức tính độ dài vectơ chi tiết nhất - Toán lớp 10 (ảnh 1)

III. Ví dụ minh họa.

Bài 1: Cho hình chữ nhật ABCD tâm O. Biết AB = 2a và AD = a. Tính độ dài $|\vec{A B} + \vec{B C}|$ .

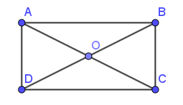
Công thức tính độ dài vectơ chi tiết nhất - Toán lớp 10 (ảnh 1)

Lời giải:

Do ABCD là hình chữ nhật nên ta có: BC = AD = a

Xét tam giác ABC vuông tại B (do ABCD là hình chữ nhật)

Áp dụng định lí Py-ta-go ta có:

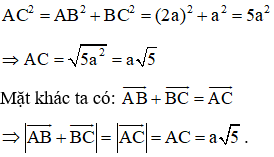
Công thức tính độ dài vectơ chi tiết nhất - Toán lớp 10 (ảnh 1)

Bài 2: Cho hình vuông ABCD cạnh a, tâm O. Tính độ dài $|\frac{1}{2} \vec{A C}|$ .

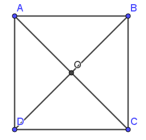
Công thức tính độ dài vectơ chi tiết nhất - Toán lớp 10 (ảnh 1)

Lời giải:

Xét tam giác ABC vuông cân tại B (do ABCD là hình vuông) :

Áp dụng định lí Py-ta-go ta có:

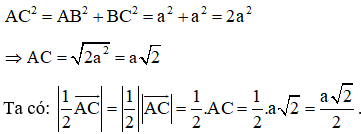
Công thức tính độ dài vectơ chi tiết nhất - Toán lớp 10 (ảnh 1)

Bài 3: Cho vectơ $\vec{a} = (1; 6 m)$ . Tìm m để độ dài $|\vec{a}| = 5$ .

Lời giải:

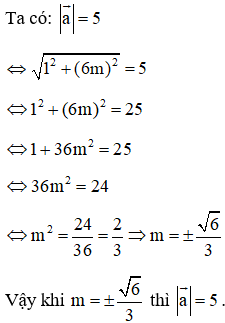
IV. Bài tập vận dụng

Bài 1: trong mặt phảng toạ độ Oxy tính khoảng cách giữa hai điểm M (1; -2) và N (-3; 4)

Hướng dẫn giải:

Áp dụng công thúc tính khoảng cách giữa hai điểm:

Ta có: MN = $\sqrt{(xN - xM)^{2} + (yn - yM)^{2}}$

= $\sqrt{(-3 - 1)^{2} + (4 -(-2))^{2}}$

= căn 52 = 2 căn 13

Bài 2: Trong mặt phẳng toạ độ Oxy cho bốn điểm A (-1; 1); B (0; 2), C (3 ; 1) và D ( 0; -2). Khẳng định nào sau đây là khẳng định đúng?

A. tứ giác ABCD là hình bình hành

N. tứ giác ABCD là hình thoi

C. tứ giác ABCD là hình thang cân

D. tứ giác ABCD không nội tiếp được hình tròn

Hướng dẫn giải:

Ta có: $\underset{AB}{\rightarrow}$ = ( 1; 1)

$\underset{DC}{\rightarrow}$ = ( 3; 3)

Suy ra: vecto DC = 3 vecto AB

Suy ra: DC // AB

do đó tứ giác ABCD là hình thang (1)

Lại có:

AC = $\sqrt{3 - (-1)^{^{2} +(1 -1( ^{^{2}}) }$ = căn 4²= 4

BD = $\sqrt{(0 -0)^{2}+ ( -2 - 2)^{2})}$ = căn 4² = 4

vậy suy ra: AC = BD (2)

Từ (1) và (2) suy ra thì ABCD là hình thang cân ( hình thang có có hai đường chéo bằng nhau là hình thang cân)

Đáp án đúng là đáp án C

Bài 3: Trong mặt phẳng toạ độ Oxy cho tam giác ABC có A(1 ; 4) ; B(3; 2) và C (5; 4) Vậy chu vi của P của tam giác đã cho bằng bao nhiêu?

A. P = 4 + 2 căn 2

B. P = 4 + 4 căn 2

C. P = 8 + 8 căn 2

D. P = 2 + 2 căn 2

Hướng dẫn giải:

Ta có:

AB = $\sqrt{(3 -1)^{2}+ (2 -4)^{2})}$ = căn 8 2 căn 2

AC = $\sqrt{(5 -1)^{2}+ (4 -4)^{2})}$ = căn 4 bình phương = 4

BC = $\sqrt{(5 -3)^{2}+ (4 - 2)^{2})}$ = căn 8 = 2 căn 2

Chu vi tam giác ABC là bằng :

P = AB + AC + BC = 2 căn 2 + 4 + 2 căn 2 = 4 + 4 căn 2

Vậy đáp án đúng là đáp án B

Bài 4: Trong mặt phẳng toạ độ Oxy cho hai điểm A (1 ;3) và B (4 ;2). Tìm toạ độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B

A. C (- 5/3 ; 0)

B. C (5/3 ; 0)

C. (-3/5 ; 0)

D. (3/5; 0)

Hướng dẫn giải:

Ta có: C thuộc Ox nên C ( x; O)

Do đó ta có:

AC = $\sqrt{(x -1 )^{2}+ (-3)^{2})}$

BC = $\sqrt{(x -4 )^{2}+ (-2)^{2})}$

Vì C cách đều hai điểm A và B nên ta có:

CA = CB

tương đường AC ²= BC ²

^{CA = CB tương đương AC 2 = BC 2}

tương đương: ( x -1 )² + (-3) ² = ( x -4 ) ² + ( -2) ²

tương đương: x² - 2x + 1 + 9 = x² - 8x + 16 + 4

tương đương ( x² - x2) + ( -2x + 8x) = 16 + 4 - 1 - 9

tương đương 6x = 10

tương đương x = 10/6

tương đương x = 5/6

Vậy C (5/3 ; 0)

Bài 5: Trong mặt phẳng toạ độ Oxy cho hai điểm A(1 ; 3) và B ( 4;2 ). Tìm toạ độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B

Bài 6: Trong mặt phẳng toạ độ Oxy cho hai điểm A (1;3) và B (4;2). Tìm toạ độ điểm C thuộc trục hoàng sao cho C cách đều hai điểm A và B

1 26,380 17/07/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: