Phương pháp giải hàm số lớp 10 và các dạng bài tập (2024) hay nhất
Với các bài toán về Hàm số lớp 10 và cách giải các dạng bài tập Toán lớp 10 Đại số gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập hàm số lớp 10 và cách giải các dạng bài tập lớp 10. Mời các bạn đón xem:
Phương pháp giải hàm số lớp 10 và các dạng bài tập hay nhất
1. Lý thuyết
a. Định nghĩa hàm số:
Cho Hàm số f xác định trên D là một qui tắc đặt tương ứng mỗi số với một và chỉ một số . Trong đó:
+) x được gọi là biến số, y được gọi là giá trị của hàm số f tại x. Kí hiệu: y = f(x).
+) D được gọi là tập xác định của hàm số.
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
b. Sự biến thiên của hàm số:
- Hàm số y = f(x) được gọi là đồng biến trên khoảng (a, b) nếu:
:
- Hàm số y = f(x) được gọi là nghịch biến trên khoảng (a, b) nếu:
:
c. Tính chẵn, lẻ của hàm số:
- Cho hàm số y = f(x) có tập xác định D.
Hàm số y = f(x) được gọi là hàm số chẵn nếu thì và f(-x) = f(x).
Hàm số y = f(x) được gọi là hàm số lẻ nếu thì và f(-x) = -f(x).
- Tính chất của đồ thị hàm số chẵn và hàm số lẻ:
Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
d. Đồ thị của hàm số:
Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng toạ độ Oxy với mọi
Chú ý: Ta thường gặp đồ thị của hàm số y = f(x) là một đường (đường thẳng, đường cong,…). Khi đó ta nói y = f(x) là phương trình của đường đó.
2. Các dạng bài tập
Dạng 1.1: Tìm tập xác định của hàm số
a. Phương pháp giải
Tập xác định của hàm số y = f(x) là tập các giá trị của x sao cho biểu thức f(x) có nghĩa. Như vậy, để tìm tập xác định chúng ta cần tìm điều kiện xác định của biểu thức f(x). Biểu thức f(x) thường là một số dạng sau:
+) . Khi đó f(x) có nghĩa khi và chỉ khi .
+) . Khi đó f(x) có nghĩa khi và chỉ khi .
+) . Khi đó f(x) có nghĩa khi và chỉ khi B(x) > 0.
+) . Khi đó f(x) có nghĩa khi và chỉ khi và B(x) > 0.
b. Ví dụ minh họa
Ví dụ 1: Tìm tập xác định của các hàm số sau:
a. .
b. .
c. .
d. .
Hướng dẫn:
a. Điều kiện xác định của hàm số là:
.
Vậy tập xác định của hàm số đã cho là: .
b. Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số đã cho là: .
c. Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số đã cho là .
d. Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số đã cho là:
Ví dụ 2: Tìm tập hợp tất cả các giá trị của m để:
a. có tập xác định là R.
b. xác định trên khoảng
Hướng dẫn:
a. Hàm số có tập xác định là R khi
Phương trình bậc hai vô nghiệm
Vậy với m < 0 thì hàm số đã cho có tập xác định là R
b. Điều kiện xác định của hàm số là:
Suy ra tập xác định của hàm số là:
Để hàm số xác định trên thì
Vậy với thì hàm số đã cho xác định trên khoảng .
Dạng 1.2: Xác định tính chẵn, lẻ của hàm số.
a. Phương pháp giải:
Các bước xét tính chẵn, lẻ của hàm số:
Bước 1: Tìm tập xác định D của hàm số.
Bước 2: Kiểm tra xem D có phải là tập đối xứng không
+) Nếu thì D là tập đối xứng, ta chuyển qua bước 3.
+) Nếu tồn tại mà thì kết luận hàm số không chẵn cũng không lẻ.
Bước 3: Xác định f(-x) và so sánh với f(x):
+ Nếu f(-x) = f(x) thì kết luận hàm số là chẵn.
+ Nếu f(-x) = -f(x) thì kết luận hàm số là lẻ.
+ Các trường hợp khác thì kết luận hàm số không chẵn cũng không lẻ.
b. Ví dụ minh họa:
Ví dụ 1: Xét tính chẵn, lẻ của hàm số sau đây:
a.
b.
c.
Hướng dẫn:
a. Tập xác định:
Ta có
Vậy hàm số đã cho là hàm số chẵn.
b. Tập xác định: .
Ta có nhưng nên hàm số không chẵn không lẻ.
c. Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số là: D = [-1; 1] \ {0}.
Ta có:
Vậy hàm số đã cho là hàm số lẻ.
Ví dụ 2: Tìm các giá trị của tham số m để hàm số là hàm số lẻ.
Hướng dẫn:
Tập xác định:
Hàm số là hàm số lẻ khi và .
Ta có:
Xét: ;
Ta có:
Vậy với m = 1 thì hàm số đã cho là hàm số lẻ.
Dạng 1.3: Xét tính đơn điệu của hàm số.
a. Phương pháp giải:
* Cách 1: Cho hàm số y = f(x) xác định trên D. Lấy và .
Đặt
+) Hàm số đồng biến trên D khi và chỉ khi T > 0.
+) Hàm số nghịch biến trên D khi và chỉ khi T < 0.
* Cách 2: Cho hàm số y = f(x) xác định trên D. Lấy và .
Đặt
+) Hàm số đồng biến trên D khi và chỉ khi T > 0.
+) Hàm số nghịch biến trên D khi và chỉ khi T < 0.
* Đối với bài tập nhìn vào bảng biến thiên để xác định tính đơn điệu của hàm số, ta dựa vào chiều mũi tên đi lên, đi xuống để xác định tính đồng biến, nghịch biến:
+) Mũi tên đi lên trong khoảng (a; b) thì hàm số đồng biến trong khoảng (a; b).
+) Mũi tên đi xuống trong khoảng (a; b) thì hàm số nghịch biến trong khoảng (a; b).
b. Ví dụ minh họa
Ví dụ 1: Xét tính đơn điệu của các hàn số sau
a.
b.
Hướng dẫn:
a.Tập xác định D = [-1; 1].
, ta có:
Với thì .
Với thì .
Vậy hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
b. Tập xác định .
, ta có:
Do đó, với và với ta đều có .
Vậy hàm số nghịch biến trên các khoảng và
Ví dụ 2: Cho hàm số có bảng biến thiên như sau:
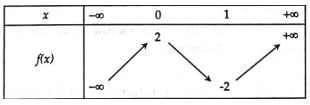
Hàm số đồng biến, nghịch biến trong các khoảng nào?
Hướng dẫn:
Trong khoảng (0; 1), mũi tên có chiều đi xuống. Do đó hàm số nghịch biến trong khoảng (0; 1).
Trong khoảng và , mũi tên có chiều đi lên. Do đó hàm số đồng biến trong khoảng và .
Dạng 1.4: Các bài tập liên quan đến đồ thị hàm số.
a. Phương pháp giải:
- Cho hàm số y = f(x) xác định trên D. Đồ thị hàm số y = f(x) là tập hợp tất cả các điểm M(x; f(x)) nằm trong mặt phẳng tọa độ với mọi
Chú ý: Điểm thuộc đồ thị hàm số y = f(x) .
- Đồ thị của hàm số chẵn nhận trục tung Oy làm trục đối xứng.
- Đồ thị của hàm số lẻ nhận gốc toạ độ O làm tâm đối xứng.
b. Ví dụ minh họa:
Ví dụ 1: Hàm số f(x) có tập xác định R và có đồ thị như hình vẽ:
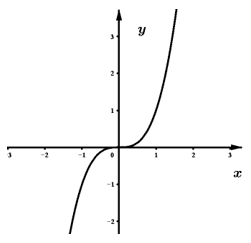
Tính giá trị biểu thức
Hướng dẫn:
Dựa vào hình dáng của đồ thị ta thấy rằng hàm số đối xứng qua O(0; 0) nên là hàm số lẻ.
Suy ra:
Vì vậy
Ví dụ 2: Cho hàm số . Có bao nhiêu điểm trên đồ thị hàm số có tung độ bằng 1?
Hướng dẫn:
Ta có:
Vậy có 3 điểm trên đồ thị hàm số có tung độ bằng 1.
3. Bài tập tự luyện
a. Tự luận
Câu 1: Tìm tất cả các giá trị của tham số m để hàm số xác định trên đoạn [3; 5].
Hướng dẫn:
Điều kiện xác định của hàm số là:
Hàm số xác định trên đoạn [3; 5]
Vậy với m < 1 hoặc m > 2 thì hàm số đã cho xác định trên đoạn [3; 5]
Câu 2: Có bao nhiêu giá trị nguyên của x thuộc tập xác định của hàm số ?
Hướng dẫn:
Tập xác định:
Do x nguyên nên .
Câu 3: Xét tính chẵn, lẻ của hàm số:
Hướng dẫn:
Tập xác định:
+ Khi x < 0 thì -x > 0 .
+ Khi x > 0 thì -x < 0 .
+ Khi thì .
Suy ra với mọi thì .
Vậy hàm số đã cho là hàm số lẻ.
Câu 4: Cho hàm số Tính .
Hướng dẫn:
Ta có:
Suy ra:
Câu 5: Xét tính đơn điệu của hàm số
Hướng dẫn:
Tập xác định:
+) Lấy sao cho . Xét:
Với và , ta có:
Do đó hàm số nghịch biến trên (1)
+) Lấy sao cho .Xét:
Với và , ta có:
Do đó hàm số nghịch biến trên (2)
Từ (1) và (2) suy ra hàm số nghịch biến trên D.
Câu 6: Tìm tập xác định của hàm số: ?
Hướng dẫn:
Hàm số xác định khi và chỉ khi (luôn đúng )
Vậy tập xác định của hàm số là R.
Câu 7: Xét tính chẵn, lẻ của hàm số .
Hướng dẫn:
Tập xác định .
Ta có:
Do đó hàm số y = f(x) là hàm số chẵn.
Câu 8: Cho hàm số:. Tính .
Hướng dẫn:
Ta có: , (do ) và (do x < 0).
Câu 9: Tìm tập xác định của hàm số
Hướng dẫn:
Hàm số đã cho xác định khi:
Vậy tập xác định của hàm số là .
Câu 10: Tìm m để hàm số xác định trên R.
Hướng dẫn:
Hàm số xác định trên R khi phương trình vô nghiệm
Hay .
b. Phần trắc nghiệm
Câu 1: Tập xác định của hàm số là:
A.
B.
C.
D.
Hướng dẫn:
Chọn D.
Hàm số là hàm đa thức nên xác định với mọi số thực x.
Câu 2: Tập xác định của hàm số là:
A.
B.
C. [0; 4].
D.
Hướng dẫn :
Chọn A.
Điều kiện xác định của hàm số là , nên tập xác định là .
Câu 3: Cho hàm số . Chọn mệnh đề đúng.
A. Hàm số trên là hàm chẵn.
B. Hàm số trên vừa chẵn vừa lẻ.
C. Hàm số trên là hàm số lẻ.
D. Hàm số trên không chẵn không lẻ.
Hướng dẫn:
Chọn A.
Đặt
Tập xác định .
Ta có và .
Vậy hàm số trên là hàm số chẵn.
Câu 4: Cho hàm số Mệnh đề nào sau đây sai?
A. Hàm số y = f(x) có tập xác định là R.
B. Đồ thị hàm số y = f(x) nhận trục tung làm trục đối xứng.
C. Hàm số y = f(x) là hàm số chẵn.
D. Đồ thị hàm số y = f(x) nhận gốc tọa độ làm tâm đối xứng.
Hướng dẫn:
Chọn D.
Tập xác định của hàm số là R.
thì , ta có:
Hàm số đã cho là hàm số chẵn, đồ thị nhận trục tung làm trục đối xứng. Do vậy các phương án A, B, C đều đúng. Đáp án D sai.
Câu 5: Chọn khẳng định đúng?
A. Hàm số y = f(x) được gọi là nghịch biến trên K nếu
B. Hàm số y = f(x) được gọi là đồng biến trên K nếu
C. Hàm số y = f(x) được gọi là đồng biến trên K nếu
D. Hàm số y = f(x) được gọi là đồng biến trên K nếu
Hướng dẫn:
Chọn D.
Lí thuyết định nghĩa hàm số đồng biến, nghịch biến.
Câu 6: Xét sự biến thiên của hàm số trên khoảng . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng .
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng .
C. Hàm số đồng biến trên khoảng .
D. Hàm số không đồng biến, không nghịch biến trên khoảng .
Hướng dẫn:
Chọn A.
, ta có:
Vậy hàm số nghịch biến trên khoảng
Câu 7: Cho hàm số có đồ thị như hình bên dưới.
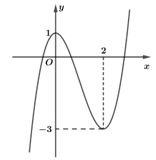
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng (0; 3).
B. Hàm số đồng biến trên khoảng
C. Hàm số nghịch biến trên khoảng (0; 2).
D. Hàm số đồng biến trên khoảng
Hướng dẫn:
Chọn C.
Trên khoảng (0; 2), đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Câu 8: Cho hàm số . Điểm nào sau đây thuộc đồ thị hàm số đã cho?
A. (-2; 0).
B. (1; 1).
C. (-2; -12).
D. (1; -1).
Hướng dẫn:
Chọn A.
Thay tọa độ điểm vào hàm số ta thấy chỉ có điểm (-2; 0) thỏa mãn.
Câu 9: Điểm nào sau đây thuộc đồ thị của hàm số ?
A. M(0; -1).
B. M(2; 1).
C. M(2; 0).
D. M(1; 1).
Hướng dẫn:
Chọn C.
Thay từng tọa độ điểm M vào hàm số . Ta thấy: với x = 2 thì y = 0.
Vậy điểm M(2; 0) thuộc đồ thị hàm số đã cho.
Câu10: Cho hàm số . Biết thì là:
A. -2.
B. 3.
C. 0.
D. 1.
Hướng dẫn:
Chọn B.
Với ta có: (loại).
Với ta có: (thỏa mãn).
Vậy .
Xem thêm các dạng bài tập Toán lớp 10 có đáp án và lời giải chi tiết khác:
Các bài toán về Số gần đúng và sai số và cách giải
Hàm số bậc nhất lớp 10 và cách giải các dạng bài tập
Hàm số bậc hai lớp 10 và cách giải các dạng bài tập
Đại cương về phương trình và cách giải bài tập
Các phương trình đưa về phương trình bậc nhất và cách giải bài tập
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)
