50 bài toán về phương trình mũ và cách giải (có đáp án 2024) – Toán 12

Phương trình mũ và cách giải các dạng bài tập - Toán lớp 12

I. LÝ THUYẾT

a. Phương trình mũ cơ bản: $a^x=b \left(a>0, a\ne 1\right)$.

* Với b >0, ta có $a^x=b \iff x={\log }_{a}b$

* Với $b\le 0$, phương trình vô nghiệm.

b. Cách giải một số phương trình mũ đơn giản.

+ Biến đổi, quy về cùng cơ số:

Đặt hai ẩn phụ đưa về phương trình tích:

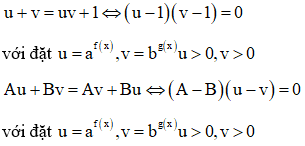
Đặt ẩn phụ đưa không hoàn toàn: là việc dùng một ẩn phụ chuyển phương trình ban đầu thành một một phương trình với một ẩn phụ mà hệ số vẫn còn ẩn rồi đưa về tích.

Đặt nhiều ẩn phụ đưa về hệ phương trình

+ Logarit hóa:

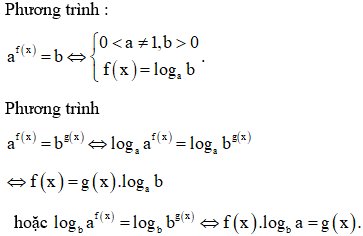
+ Giải bằng phương pháp đồ thị:

Giải phương trình:

$\left(0<a\ne 1\right)a^x=f\left(x\right)$$\left(*\right)$

Xem phương trình $\left(*\right)$ là phương trình hoành độ giao điểm của hai đồ thị $y=a^x$ $\left(0<a\ne 1\right)$ và $y=f\left(x\right)$. Khi đó ta thực hiện hai bước:

Bước 1. Vẽ đồ thị các hàm số

$y=a^x\left(0<a\ne 1\right)và y=f\left(x\right)$

Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.

+ Sử dụng tính đơn điệu của hàm số:

Tính chất 1. Nếu hàm số $y=f\left(x\right)$ luôn đồng biến (hoặc luôn nghịch biến) trên (a,b) thì số nghiệm của phương trình $f\left(x\right)=k$ trên (a,b) không nhiều hơn một và $f\left(u\right)=f\left(v\right)\iff u=v,\forall u,v\in \left(a;b\right)$

Tính chất 2. Nếu hàm số $y=f\left(x\right)$ liên tục và luôn đồng biến (hoặc luôn nghịch biến); hàm số $y=g\left(x\right)$ liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên D thì số nghiệm trên D của phương trình $f\left(x\right)=g\left(x\right)$ không nhiều hơn một.

Tính chất 3. Nếu hàm số $y=f\left(x\right)$ luôn đồng biến (hoặc luôn nghịch biến) trên D thì bất phương trình $f\left(u\right)>f\left(v\right)\iff u>v$ ( hoặc u < v)$\forall u,v\in D$.

+ Sử dụng đánh giá:

Giải phương trình $f\left(x\right)=g\left(x\right)$.

Nếu ta đánh giá được $\left\{\begin{array}{c}f\left(x\right)\ge m\\ g\left(x\right)\le m\end{array}\right.$ thì :

$$\begin{gathered} f\left(x\right)=g\left(x\right) \\ \iff \left\{\begin{array}{c}f\left(x\right)=m\\ g\left(x\right)=m\end{array}\right. \end{gathered}$$

II. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1. Phương trình mũ cơ bản

A. Phương pháp

$a^x=b \left(a>0, a\ne 1\right)$. Để giải pt trên, ta sử dụng định nghĩa logarit.

* Với $b>0$, ta có $a^x=b \iff x={\log }_{a}b$

* Với $b\le 0$, phương trình vô nghiệm.

B. Ví dụ minh họa

Câu 1. Phương trình $3^{\frac{1}{x}}=4$ có nghiệm là

A. $x={\log }_{2}3$

B. $x={\log }_{3}2$.

C. $x={\log }_{4}3$

D. $x={\log }_{3}4$.

Hướng dẫn giải

Chọn C.

Ta có :

$$\begin{gathered} 3^{\frac{1}{x}}=4\iff \frac{1}{x}={\log }_{3}4 \\ \iff x={\log }_{4}3 \end{gathered}$$

Câu 2. Phương trình $8^x=4$ có nghiệm là

A. $x=\frac{2}{3}$

B. $x=-\frac{1}{2}$

C. $x=\frac{1}{2}$

D. $x=-2$.

Hướng dẫn giải

Chọn A.

Ta có:

$$\begin{gathered} 8^x=4\iff x={\log }_{8}4 \\ \iff x={\log }_{2^3}{2}^2=\frac{2}{3} \end{gathered}$$

Câu 3. Nghiệm của phương trình $2^x+2^{x+1}=3^x+3^{x+1}$ là:

A. $x={\log }_{\frac{3}{2}}\frac{3}{4}$

B. $x=1$

C. $x=0$

D. $x={\log }_{\frac{4}{3}}\frac{2}{3}$.

Hướng dẫn giải

$$\begin{gathered} 2^x+2^{x+1}=3^x+3^{x+1} \\ \iff {3.2}^x={4.3}^x\iff {\left(\frac{3}{2}\right)}^x=\frac{3}{4} \\ \iff x={\log }_{\frac{3}{2}}\frac{3}{4} \end{gathered}$$

Chọn A.

Câu 4. Nghiệm của phương trình ${12.3}^x+{3.15}^x-5^{x+1}=20$ là:

A. $x={\log }_{3}5-1$

B. $x={\log }_{3}5$

C. $x={\log }_{3}5+1$

D. $x={\log }_{5}3-1$.

Hướng dẫn giải

$$\begin{gathered} {12.3}^x+{3.15}^x-5^{x+1}=20 \\ \iff {3.3}^x\left(5^x+4\right)-5\left(5^x+4\right)=0 \\ \iff \left(5^x+4\right)\left(3^{x+1}-5\right)=0 \\ \iff 3^{x+1}=5\iff x={\log }_{3}5-1 \end{gathered}$$

Chọn A.

Câu 5. Phương trình $3^{x-2}=\frac{3}{9^x}$ có nghiệm là

A. $x=1$

B. $x=0$

C. $x=-1$

D. $x=3$.

Hướng dẫn giải

Chọn A.

$$\begin{gathered} 3^{x-2}=\frac{3}{9^x}\iff 3^{x-2}=3^{1-2x} \\ \iff x-2=1-2x\iff x=1 \end{gathered}$$

Nghiệm của phương trình là $x=1$

Câu 6. Tập nghiệm của ph­ương trình $2^{x^2-x-4}=\frac{1}{16}$ là

A. $\left\{-2;2\right\}.$

B. $\varnothing .$

C. $\left\{2;4\right\}.$

D. $\left\{0;1\right\}.$

Hướng dẫn giải

Chọn D.

Ta có:

$$\begin{gathered} 2^{x^2-x-4}=2^{-4} \\ \iff x^2-x-4=-4 \\ \iff x^2-x=0\iff \left[\begin{array}{l}x=0\\ x=1\end{array}\right. \end{gathered}$$

Câu 7. Giải phương trình $3^{x-4}={\left(\frac{1}{9}\right)}^{3x-1}.$

A. $x=\frac{6}{7}.$

B. $x=1.$

C. $x=\frac{1}{3}.$

D. $x=\frac{7}{6}.$

Hướng dẫn giải

Chọn A.

Ta có:

$$\begin{gathered} 3^{x-4}={\left(\frac{1}{9}\right)}^{3x-1} \\ \iff 3^{x-4}=3^{-6x+2} \\ \iff x-4=-6x+2 \\ \iff x=\frac{6}{7}. \end{gathered}$$

Câu 8. Phương trình $3^x{.5}^{x-1}=7$ có nghiệm là

A. ${\log }_{15}35.$

B. ${\log }_{21}5.$

C. ${\log }_{21}35.$

D. ${\log }_{15}21.$

Hướng dẫn giải

Chọn A.

$PT \iff {15}^x=35\iff x={\log }_{15}35$

Dạng 2. Phương pháp đưa về cùng cơ số

A. Phương pháp

$a^{f\left(x\right)}=a^{g\left(x\right)}\iff a=1$

hoặc $\left\{\begin{array}{c}0<a\ne 1\\ f\left(x\right)=g\left(x\right)\end{array}\right.$.

B. Ví dụ minh họa

Câu 1. Tìm tập nghiệm của phương trình $2^{{\left(x-1\right)}^2}=4^x$.

A. $\left\{4+\sqrt{3},4-\sqrt{3}\right\}$

B. $\left\{2+\sqrt{3},2-\sqrt{3}\right\}$

C. $\left\{-4+\sqrt{3},-4-\sqrt{3}\right\}$

D. $\left\{-2+\sqrt{3},-2-\sqrt{3}\right\}$

Hướng dẫn giải

Chọn B.

Ta có :

$$\begin{gathered} 2^{{\left(x-1\right)}^2}=4^x\iff 2^{{\left(x-1\right)}^2}=2^{2x} \\ \iff {\left(x-1\right)}^2=2x \\ \iff x^2-4x+1=0 \\ \iff \left[\begin{array}{l}x=2+\sqrt{3}\\ x=2-\sqrt{3}\end{array}\right. \end{gathered}$$

Vậy tập ngiệm của phương trình: $S=\left\{2-\sqrt{3};2+\sqrt{3}\right\}.$

Câu 2. Nghiệm của phương trình ${\left(\frac{1}{25}\right)}^{x+1}={125}^x$ là:

A.$-\frac{2}{5}$

B. 4

C. $-\frac{1}{8}$

D. 1

Hướng dẫn giải

Chọn A.

Ta có :

$$\begin{gathered} {\left(\frac{1}{25}\right)}^{x+1}={125}^x \\ \iff 5^{-2\left(x+1\right)}=5^{3x} \\ \iff -2\left(x+1\right)=3x \\ \iff x=-\frac{2}{5} \end{gathered}$$

Vậy phương trình có nghiệm là $x=-\frac{2}{5}$.

Câu 3. Phương trình ${\left(0.2\right)}^{x+2}={\left(\sqrt{5}\right)}^{4x-4}$ tương đương với phương trình:

A. $5^{-x+2}=5^{2x-2}$

B. $5^{-x-2}=5^{2x-2}$

C. $5^{-x-2}=5^{2x-4}$

D. $5^{-x+2}=5^{2x-4}$.

Hướng dẫn giải

Chọn B.

$$\begin{gathered} {\left(0.2\right)}^{x+2}={\left(\sqrt{5}\right)}^{4x-4} \\ \iff {\left(\frac{1}{5}\right)}^{x+2}=5^{2x-2} \\ \iff 5^{-x-2}=5^{2x-2} \end{gathered}$$

Câu 4. Phương trình $2^{2x-1}-\frac{1}{8}=0$ có nghiệm là

A. $x=-1$

B. $x=2$

C. $x=-2$

D. $x=1$

Hướng dẫn giải

Chọn A.

Ta có :

$$\begin{gathered} 2^{2x-1}-\frac{1}{8}=0 \\ \iff 2^{2x-1}=2^{-3} \\ \iff x=-1 \end{gathered}$$

Vậy phương trình có nghiệm là x = -1.

Câu 5. Gọi là tổng các nghiệm của phương trình ${\left(3^x\right)}^{x-1}=64$ thì giá trị của S là

A. $\frac{1}{2}$

B. -6

C. -3

D. 1

Hướng dẫn giải

Chọn D.

Ta có

$$\begin{gathered} {\left(2^x\right)}^{x-1}=64\iff 2^{x\left(x-1\right)}=64 \\ \iff x^2-x=6\iff x^2-x-6=0 \\ \iff \left[\begin{array}{c}x=3\\ x=-2\end{array}\right.\Rightarrow S=1 \end{gathered}$$

Câu 6. Tìm tập nghiệm S của phương trình $5^{2x^2-x}=5$.

A. $S=\varnothing$

B. $S=\left\{0;\frac{1}{2}\right\}$

C. $S=\left\{0;2\right\}$

D. $S=\left\{1;-\frac{1}{2}\right\}$

Hướng dẫn giải

Chọn D.

Phương trình đã cho tương đương với $2x^2-x=1$

$$\begin{gathered} \iff 2x^2-x-1=0 \\ \iff x=1\vee x=-\frac{1}{2} \end{gathered}$$

Vậy tập nghiệm của phương trình : $S=\left\{1;-\frac{1}{2}\right\}$.

Câu 7. Nghiệm của phương trình $4^{2x-m}=8^x$ là

A. $x=-m$

B. $x=-2m$

C. $x=2m$

D. $x=m$

Hướng dẫn giải

Chọn C.

Ta có:

$$\begin{gathered} 4^{2x-m}=8^x\iff {\left(2^2\right)}^{2x-m}={\left(2^3\right)}^x \\ \iff 2^{4x-2m}=2^{3x} \\ \iff 4x-2m=3x\iff x=2m \end{gathered}$$

Vậy nghiệm của phương trình x = 2m.

Câu 8. Tập nghiệm của phương trình ${\left(\frac{3}{2}\right)}^{2-2x}={\left(\frac{8}{27}\right)}^{x-2}$ là

A. $\left\{\frac{8}{5}\right\}$

B. $\left\{\frac{8}{3}\right\}$

C. $\left\{4\right\}$

D. $\left\{2\right\}$.

Hướng dẫn giải

Chọn C

$$\begin{gathered} {\left(\frac{3}{2}\right)}^{2-2x}={\left(\frac{8}{27}\right)}^{x-2} \\ \iff {\left(\frac{3}{2}\right)}^{2-2x}={\left(\frac{3}{2}\right)}^{-3.(x-2)} \\ \iff 2-2x=-3\left(x-2\right) \\ \iff 3x-2x=6-2\iff x=4 \end{gathered}$$

Vậy tập nghiệm của phương trình: S = {4}.

Dạng 3. Phương pháp đăt ẩn phụ

A. Phương pháp

$$\begin{gathered} f\left[a^{g\left(x\right)}\right]=0 \left(0<a\ne 1\right) \\ \iff \left\{\begin{array}{c}t=a^{g\left(x\right)}>0\\ f\left(t\right)=0\end{array}\right. \end{gathered}$$

Ta thường gặp các dạng:

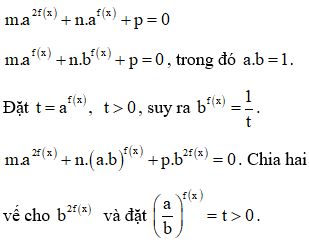
Đặt hai ẩn phụ đưa về phương trình tích:

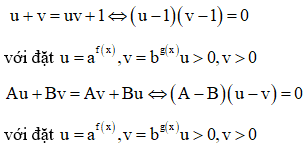
Đặt ẩn phụ đưa không hoàn toàn: là việc dùng một ẩn phụ chuyển phương trình ban đầu thành một một phương trình với một ẩn phụ mà hệ số vẫn còn ẩn x rồi đưa về tích.

Đặt nhiều ẩn phụ đưa về hệ phương trình: Đặt ẩn phụ sau đó dựa vào các điều kiện để đưa phương trình đã cho về hệ phương trình với các ẩn mới.

B. Ví dụ minh họa

Câu 1. Cho phương trình $4^x-4^{1-x}=3$. Khẳng định nào sau đây sai?

A. Phương trình vô nghiệm.

B. Phương trình có một nghiệm.

C. Nghiệm của phương trình là luôn lớn hơn 0.

D. Phương trình đã cho tương đương với phương trình: $4^{2\text{x}}-{3.4}^x-4=0$.

Hướng dẫn giải

Ta có:

$$\begin{gathered} 4^x-4^{1-x}=3 \\ \iff 4^x-\frac{4}{4^x}=3 \end{gathered}$$

Đặt $t=4^x$(t >0), khi đó phương trình đã cho tương đương với

$$\begin{gathered} t-\frac{4}{t}=3\iff t^2-3t-4=0 \\ \iff \left[\begin{array}{l}t=4\\ t=-1\left(L\right)\end{array}\right. \\ \iff 4^x=4\iff x=1. \end{gathered}$$

Vậy phương trình đã cho có một nghiệm, nghiệm này lớn hơn 0. Do đó A sai.

Chọn A.

Câu 2. Cho phương trình $3^{2x+10}-{6.3}^{x+4}-2=0\left(1\right)$. Nếu đặt $t=3^{x+5}\left(t>0\right)$ thì (1) trở thành phương trình nào?

A. $9t^2-6t-2=0.$

B. $t^2-2t-2=0.$

C. $t^2-18t-2=0.$

D. $9t^2-2t-2=0.$

Hướng dẫn giải

Chọn B.

$$\begin{gathered} 3^{2x+10}-{6.3}^{x+4}-2=0 \\ \iff 3^{2\left(x+5\right)}-{2.3}^{x+5}-2=0 \end{gathered}$$

Vậy khi đặt $t=3^{x+5}\left(t>0\right)$ thì (1) trở thành phương trình $t^2-2t-2=0.$

Câu 3. Phương trình $9^x-{5.3}^x+6=0$ có tổng các nghiệm là:

A. ${\log }_{3}6$

B. ${\log }_3\frac{2}{3}$

C. ${\log }_3\frac{3}{2}$

D. $-{\log }_{3}6$

Hướng dẫn giải

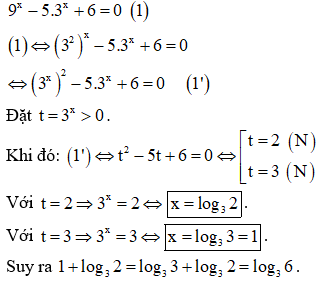
Chọn A.

Câu 4. Cho phương trình $2^{1+2x}+{15.2}^x-8=0$, khẳng định nào sau dây đúng?

A. Có một nghiệm.

B. Vô nghiệm.

C. Có hai nghiệm dương.

D. Có hai nghiệm âm.

Hướng dẫn giải

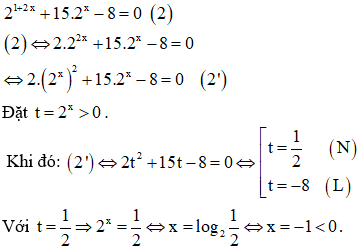
Do đó A đúng.

Chọn A.

Câu 5. Phương trình $5^{x-1}+5.{\left(0,2\right)}^{x-2}=26$ có tổng các nghiệm là:

A. 1

B. 4

C. 2

D. 3.

Hướng dẫn giải

Chọn B.

[Phương pháp tự luận]

$$\begin{gathered} 5^{x-1}+5.{\left(0,2\right)}^{x-2}=26 \\ \iff 5^{x-1}+{5.5}^{2-x}=26 \\ \iff 5^{x-1}+{25.5}^{1-x}=26 \end{gathered}$$

Đặt $t=5^{x-1}\left(t>0\right)$, phương trình trở thành:

$$\begin{gathered} t+\frac{25}{t}=26 \\ \iff t^2-26t+25=0 \\ \iff \left[\begin{array}{l}t=1\\ t=25\end{array}\right.\iff \left[\begin{array}{l}{5}^{x-1}=1\\ 5^{x-1}=25\end{array}\right. \\ \iff \left[\begin{array}{l}x=1\\ x=3\end{array}\right. \end{gathered}$$

Vậy tổng các nghiệm là 4.

[Phương pháp trắc nghiệm]

Nhập vào máy tính $5^{x-1}+5.{\left(0,2\right)}^{x-2}-26$. Nhấn dấu = để lưu phương trình.

Shift $\to$ Solve $\to$0$\to$=. Ra nghiệm .

Shift$\to$ Solve $\to$4$\to$ =. Ra nghiệm .

Câu 6. Cho phương trình $9^{x^2+x-1}-{10.3}^{x^2+x-2}+1=0.$ Tổng tất cả các nghiệm của phương trình là:

A. -2

B. 2

C. 1

D. 0.

Hướng dẫn giải

Đặt $t=3^{x^2+x-1}$ ($t>0$), khi đó phương trình đã cho tương đương với

$$\begin{gathered} 3t^2-10t+3=0\iff \left[\begin{array}{l}t=3\\ t=\frac{1}{3}\end{array}\right. \\ \iff \left[\begin{array}{l}{3}^{x^2+x-1}=3\\ 3^{x^2+x-1}=\frac{1}{3}\end{array}\right. \\ \iff \left[\begin{array}{l}{x}^2+x-1=1\\ x^2+x-1=-1\end{array}\right. \\ \iff \left[\begin{array}{l}x=-2\\ x=1\\ x=0\\ x=-1\end{array}\right. \end{gathered}$$

Vậy tổng tất cả các nghiệm của phương trình bằng -2

Câu 7. Tìm tích các nghiệm của phương trình ${\left(\sqrt{2}-1\right)}^x+{\left(\sqrt{2}+1\right)}^x-2\sqrt{2}=0$

A. 2

B. -1

C. 0

D. 1.

Hướng dẫn giải

Chọn B.

Câu 8. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình $4^x+\left(1-3m\right)2^x+2m^2-m=0$ có nghiệm.

A. $\left(-\infty ;+\infty \right)$

B. $\left(-\infty ;1\right)\cup \left(1;+\infty \right)$

C. $\left(0;+\infty \right)$

D. $\left(\frac{1}{2};+\infty \right)$

Hướng dẫn giải

Chọn C.

Xét phương trình:

$4^x+\left(1-3m\right)2^x+2m^2-m=0\left(1\right)$

Đặt $t=2^x,t>0.$ Phương trình (1) trở thành:

$t^2+\left(1-3m\right)t+2m^2-m=0\left(2\right)$

Phương trình (2) luôn có 2 nghiệm:

$x=m;x=2m-1,\forall m.$

Phương trình (1) có nghiệm thực khi và chỉ khi phương trình (2) có nghiệm t >0

Từ đó suy ra:

$\left[\begin{array}{l}m>0\\ 2m-1>0\end{array}\right.\Rightarrow m\in \left(0;+\infty \right).$

Dạng 4. Phương pháp logarit hóa

A. Phương pháp:

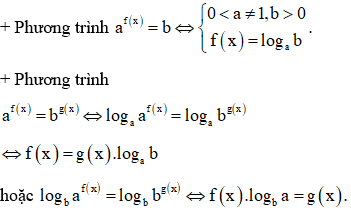
B. Ví dụ minh họa:

Câu 1. Biết rằng phương trình $2^{x^2-1}=3^{x+1}$ có 2 nghiệm là a,b. Khi đó a + b +ab có giá trị bằng

A. $-1+2{\log }_{2}3$

B. $1+{\log }_{2}3$

C. -1

D. $1+2{\log }_{2}3$.

Hướng dẫn giải.

Chọn C.

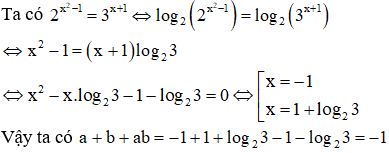
Câu 2. Phương trình $2^{x-3}=3^{x^2-5x+6}$ có hai nghiệm $x_1,x_2$ trong đó $x_1<x_2$, hãy chọn phát biểu đúng?

A. $3x_1-2x_2={\log }_{3}8$

B. $2x_1-3x_2={\log }_{3}8$

C. $2x_1+3x_2={\log }_{3}54.$

D. $3x_1+2x_2={\log }_{3}54.$

Hướng dẫn giải

Logarit hóa hai vế của phương trình (theo cơ số 2) ta được:

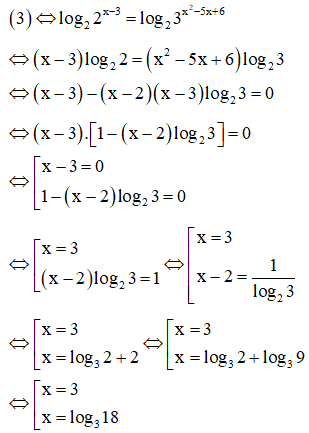
Câu 3. Cho hai số thực dương lớn hơn 1 và biết phương trình $a^{x^2}{b}^{x+1}=1$ có nghiệm thực. Tìm giá trị nhỏ nhất của biểu thức $P={\log }_a\left(ab\right)+\frac{4}{{\log }_{a}b}$.

A. 4

B. 5

C. 6

D. 10

Hướng dẫn giải

Phương trình tương đương với:

$$\begin{gathered} x^2+\left(x+1\right){\log }_{a}b=0 \\ \iff x^2+x{\log }_{a}b+{\log }_{a}b=0 \end{gathered}$$

Điều kiện để phương trình có nghiệm là:

$$\begin{gathered} \Delta ={\left({\log }_{a}b\right)}^2-4{\log }_{a}b\ge 0 \\ \iff {\log }_{a}b\ge 4\left({\log }_{a}b>0\right) \end{gathered}$$

Khi đó:

$$\begin{gathered} P={\log }_{a}b+\frac{4}{{\log }_{a}b}+1 \\ =f\left(t\right)=t+\frac{4}{t}+1\ge {\min }_{\left[4;+\infty \right)}f\left(t\right) \\ =f\left(4\right)=6 \end{gathered}$$

Với $t={\log }_{a}b\ge 4$.

Chọn C.

Câu 4. Cho các số nguyên dương a,b lớn hơn 1. Biết phương trình $a^{x^2+1}=b^x$ có hai nghiệm phân biệt $x_1,x_2$ và phương trình $b^{x^2-1}={\left(9a\right)}^x$ có hai nghiệm phân biệt $x_3,x_4$ thỏa mãn $\left(x_1+x_2\right)\left(x_3+x_4\right)<3$. Tìm giá trị nhỏ nhất của biểu thức $S=3a+2b$.

A. 12

B. 46

C. 44

D. 22

Hướng dẫn giải

Chọn B.

Dạng 5. Phương pháp đồ thị, hàm số, đánh giá

A. Phương pháp

+ Giải bằng phương pháp đồ thị:

Giải phương trình:

$a^x=f\left(x\right)\left(0<a\ne 1\right)\left(*\right)$

Xem phương trình $\left(*\right)$ là phương trình hoành độ giao điểm của hai đồ thị $y=a^x\left(0<a\ne 1\right)$ và $y=f\left(x\right)$. Khi đó ta thực hiện hai bước:

Bước1. Vẽ đồ thị các hàm số

$y=a^x\left(0<a\ne 1\right)$ và $y=f\left(x\right)$

Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.

+ Sử dụng tính đơn điệu của hàm số:

Tính chất 1. Nếu hàm số $y=f\left(x\right)$ luôn đồng biến (hoặc luôn nghịch biến) trên (a,b) thì số nghiệm của phương trình $f\left(x\right)=k$ trên(a,b) không nhiều hơn một và $f\left(u\right)=f\left(v\right)\iff u=v,\forall u,v\in \left(a;b\right)$

Tính chất 2. Nếu hàm số $y=f\left(x\right)$ liên tục và luôn đồng biến (hoặc luôn nghịch biến); hàm số $y=g\left(x\right)$ liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên D thì số nghiệm trên D của phương trình $f\left(x\right)=g\left(x\right)$ không nhiều hơn một.

Tính chất 3. Nếu hàm số $y=f\left(x\right)$ luôn đồng biến (hoặc luôn nghịch biến) trên D thì bất phương trình $f\left(u\right)>f\left(v\right)\iff u>v$ ( hoặc u <v), $\forall u,v\in D$.

+ Sử dụng đánh giá:

Giải phương trình $f\left(x\right)=g\left(x\right)$.

Nếu ta đánh giá được $\left\{\begin{array}{c}f\left(x\right)\ge m\\ g\left(x\right)\le m\end{array}\right.$ thì :

$f\left(x\right)=g\left(x\right)\iff \left\{\begin{array}{c}f\left(x\right)=m\\ g\left(x\right)=m\end{array}\right.$

B. Ví dụ minh họa

Câu 1. Phương trình $\left(x-1\right){.2}^x=x+1$ có bao nhiêu nghiệm thực

A. 1

B. 0

C. 3

D. 2

Hướng dẫn giải

Chọn D.

Vì không là nghiệm của phương trình nên ta có:

$$\begin{gathered} \left(x-1\right){.2}^x=x+1 \\ \iff 2^x=\frac{x+1}{x-1} \end{gathered}$$

Hàm số $y=2^x$ đồng biến trên R, hàm số $y=\frac{x+1}{x-1}$ nghịch biến trên $\left(-\infty ;1\right)$ và $\left(1;+\infty \right)$.

Do đó phương trình đã cho có hai nghiệm.

Câu 2. Với giá trị nào của tham số m thì bất phương trình $2^{{\sin }^{2}x}+3^{{\text{cos}}^{2}x}\ge m{.3}^{{\sin }^{2}x}$ có nghiệm?

A. $m\le 4.$

B. $m\ge 4$

C. $m\le 1.$

D. $m\ge 1.$

Hướng dẫn giải

Chia hai vế của bất phương trình cho $3^{{\sin }^{2}x}>0$, ta được

${\left(\frac{2}{3}\right)}^{{\sin }^{2}x}+3.{\left(\frac{1}{9}\right)}^{{\sin }^{2}x}\ge m$

Xét hàm số $y={\left(\frac{2}{3}\right)}^{{\sin }^{2}x}+3.{\left(\frac{1}{9}\right)}^{{\sin }^{2}x}$ là hàm số nghịch biến.

Ta có: $0\le {\sin }^{2}x\le 1$nên $1\le y\le 4$

Vậy bất phương trình có nghiệm khi $m\le 4$.

Chọn A.

Câu 3. Số nghiệm của phương trình $2x^2+2x-9=\left(x^2-x-3\right){.8}^{x^2+3x-6}+\left(x^2+3x-6\right){.8}^{x^2-x-3}$ là

A. 1

B. 3

C. 2

D. 4

Hướng dẫn giải

Chọn D

Phương trình đã cho

Vậy phương trình đã cho có 4 nghiệm phân biệt.

Hoặc biến đổi $\left(*\right)\iff \frac{8^u-1}{u}+\frac{8^v-1}{v}=0,$

dễ thấy $\frac{8^u-1}{u}>0;\forall u\ne 0$ (Table = Mode 7).

Câu 4. Tìm tất cả các giá trị của m để hàm số $3^x=mx+1$ có hai nghiệm phân biệt?

A. $m>0$

B. $\left\{\begin{array}{l}m>0\\ m\ne \ln 3\end{array}\right.$

C. $m\ge 2$

D. Không tồn tại m.

Hướng dẫn giải

Chọn B.

Ta có: $3^x=mx+1$ là phương trình hoành độ giao điểm của $y=3^x$ và $y=mx+1$.

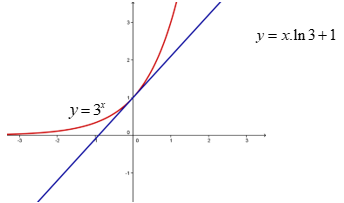
Ta thấy $y=mx+1$ luôn đi qua điểm cố định (0;1) nên

+ Nếu m <0 thì $y=mx+1$ là hàm nghịch biến nên có đồ thị cắt đồ thị hàm số $y=3^x$ tại một điểm duy nhất.

+ Nếu m >0 thì để đồ thị hàm số $y=mx+1$ cắt đồ thị hàm số $y=3^x$ tại hai điểm phân biệt thì phải khác tiếp tuyến của đồ thị hàm số $y=3^x$ tại điểm (0;1), tức là $m\ne \ln 3$.

Vậy $\left\{\begin{array}{l}m>0\\ m\ne \ln 3\end{array}\right..$

III. BÀI TẬP TỰ LUYỆN

Câu 1. Tìm các nghiệm của phương trình $2^{x-2}=8^{100}$.

A. $x=204$

B. $x=102$

C. $x=302$

D. $x=202$.

Câu 2. Tìm nghiệm của phương trình $2^x={\left(\sqrt{3}\right)}^x.$

A. $x=1$

B. $x=-1$

C. $x=0$

D. $x=2$

Câu 3. Số nghiệm của phương trình $2^{2x^2-7x+5}=1$ là:

A. 3

B. 0

C. 1

D. 2.

Câu 4. Cho phương trình: $3^x=m+1$. Chọn phát biểu đúng

A. Phương trình luôn có nghiệm với mọi m.

B. Phương trình có nghiệm với $m\ge -1$.

C. Phương trình có nghiệm dương nếu $m>0$.

D. Phương trình luôn có nghiệm duy nhất $x={\log }_3\left(m+1\right)$.

Câu 5. Phương trình $2^{x^2-9x+16}=4$ có nghiệm là

A. $x=2,x=7$

B. $x=4,x=5$

C. $x=1,x=8$

D. $x=3,x=6$

Câu 6. Tổng các nghiệm của phương trình $3^{x^4-3x^2}=81$.

A. 0

B. 1

C. 3

D. 4.

Câu 7. Tìm nghiệm của phương trình $\frac{3^{2x-6}}{27}={\left(\frac{1}{3}\right)}^x.$

A. $x=4$

B. $x=2$

C. $x=5$

D. $x=3$.

Câu 8. Tìm nghiệm của phương trình $4^{2x+5}=2^{2-x}$.

A. $-\frac{8}{5}$

B. $\frac{12}{5}$

C. 3

D. $\frac{8}{5}$

Câu 9. Tổng bình phương các nghiệm của phương trình $5^{3x-2}={\left(\frac{1}{5}\right)}^{-x^2}$ bằng:

A. 0

B. 5

C. 2

D. 3

Câu 10. Tổng các nghiệm của phương trình $3^{x^4-3x^2}=81$ bằng

A. 0

B. 1

C. 3

D. 4

Câu 11. Cho phương trình: ${2.3}^{x+1}-{15}^x+{2.5}^x=12$, giá trị nào gần với tổng 2 nghiệm của phương trình trên nhất?

A. 1,75

B. 1,74

C. 1,73

D. 1,72

Câu 12. Số nghiệm của phương trình ${\left|x-3\right|}^{x^2-x}={\left(x-3\right)}^{12}$ là:

A. 4.

B. 1.

C. 2.

D. 3.

Câu 13. Tổng các nghiệm của phương trình $2^{2x-3}-{3.2}^{x-2}+1=0$ là

A. 6

B. 3

C. 5

D. -4.

Câu 14. Giải phương trình $4^x-{6.2}^x+8=0$.

A. x =1.

B. x =0, x=2.

C. x =1, x=2.

D. x =2.

Câu 15. Phương trình $9^x-{3.3}^x+2=0$ có hai nghiệm $x_1,x_2$ với $x_1<x_2$. Giá trị $A=2x_1+3x_2$ là

A. $2{\log }_{2}3$

B. 1.

C. $3{\log }_{3}2$

D. $4{\log }_{3}2$.

Câu 16. Phương trình ${\left(3+\sqrt{5}\right)}^x+{\left(3-\sqrt{5}\right)}^x={3.2}^x$ có tổng các nghiệm là

A. 0.

B. 10.

C. 1

D. 2

Câu 17. Tìm tích tất cả các nghiệm của phương trình ${4.3}^{\log \left(100x^2\right)}+{9.4}^{\log \left(10x\right)}={13.6}^{1+\log x}$

A. 100

B. 10

C. 1

D. $\frac{1}{10}.$

Câu 18. Tính tổng tất cả các nghiệm của phương trình $4^{x^2-3x+2}+4^{x^2+6x+5}=4^{2x^2+3x+7}+1$

A. -3

B. -2

C. - 7

D. 7

Câu 19. Cho phương trình ${\left(7+4\sqrt{3}\right)}^x+{\left(2+\sqrt{3}\right)}^x=6$. Khẳng định nào sau đây là đúng?

A. Phương trình có một nghiệm vô tỉ.

B. Phương trình có một nghiệm hữu tỉ.

C. Phương trình có hai nghiệm trái dấu.

D. Tích của hai nghiệm bằng -6.

Câu 20. Tìm m để phương trình $4^{x^2}-2^{x^2+2}+6=m$ có đúng 3 nghiệm thực phân biệt.

A. $m>3$

B. $m=3$

C. $2<m<3$

D. $m=2$.

Câu 21. Có bao nhiêu giá trị thực của tham số m để phương trình $m\cdot 3^{x^2-3x+2}+3^{4-x^2}=3^{6-3x}+m$ có đúng 3 nghiệm thực phân biệt.

A. 2

B. 4

C. 1

D. 3

Câu 22. Hỏi phương trình ${3.2}^x+{4.3}^x+{5.4}^x={6.5}^x$ có tất cả bao nhiêu nghiệm thực?

A. 2

B. 4

C. 1.

D. 3.

Câu 23. Biết phương trình $9^x-2^{x+\frac{1}{2}}=2^{x+\frac{3}{2}}-3^{2x-1}$ có nghiệm là a. Tính giá trị biểu thức $P=a+\frac{1}{2}{\log }_{\frac{9}{2}}2.$

A. $P=\frac{1}{2}.$

B. $P=1-{\log }_{\frac{9}{2}}2.$

C. $P=1.$

D. $P=1-\frac{1}{2}{\log }_{\frac{9}{2}}2.$

Câu 24. Cho số thực $a>1,b>1$. Biết phương trình $a^x{b}^{x^2-1}=1$ có hai nghiệm phân biện $x_1,x_2$. Tìm giá trị nhỏ nhất của biểu thức $S={\left(\frac{x_1{x}_2}{x_1+x_2}\right)}^2-4\left(x_1+x_2\right)$.

A. 4

B. $3\sqrt[3]{2}$

C. $3\sqrt[3]{4}$

D. $\sqrt[3]{4}$

Câu 25. Phương trình ${\left(\sqrt{3}-\sqrt{2}\right)}^x+{\left(\sqrt{3}+\sqrt{2}\right)}^x={\left(\sqrt{10}\right)}^x$ có tất cả bao nhiêu nghiệm thực?

A. 1

B. 2

C. 3.

D. 4.

Câu 26. Phương trình $3^{2x}+2x\left(3^x+1\right)-{4.3}^x-5=0$ có tất cả bao nhiêu nghiệm không âm?

A. 1

B. 2

C. 0

D. 3

Câu 27. Tìm số nghiệm của phương trình $2^x+3^x+4^x+\mathrm{...}+{2016}^x+{2017}^x=2016-x$

A. 1.

B. 2016.

C. 2017.

D. 0.

Câu 28. Tìm các giá trị của m để phương trình: $\sqrt{3^x+3}+\sqrt{5-3^x}=m$ có 2 nghiệm phân biệt:

A. $\sqrt{3}+\sqrt{5}<m<4$

B. $2\sqrt{2}<m<4$

C. $2\sqrt{2}<m<\sqrt{3}$

D. $m>2\sqrt{2}$.

Câu 29. Phương trình $4^{x^2}-2^{{\left(x+1\right)}^2}=2x+1-x^2$ có bao nhiêu nghiệm dương.

A. 3.

B. 1

C. 2.

D. 0.

Câu 30. Cho phương trình $5^{x^2+2mx+2}-5^{2x^2+4mx+2}-x^2-2mx=0$.Tìm m để phương trình vô nghiệm?

A. $m>0$

B. $m<1$

C. Không có m.

D. $\left[\begin{array}{l}m>1\\ m<0\end{array}\right.$

Đáp án