Nội dung bài viết

    Xem thêm

    Công thức tính diện tích thiết diện hình nón chi tiết nhất – Toán 12

    Với Công thức tính diện tích thiết diện hình nón chi tiết nhất Toán lớp 12 Hình học chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ Công thức tính diện tích thiết diện hình nón chi tiết nhất biết cách làm bài tập Toán 12. Mời các bạn đón xem:

    1 9,594 18/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12

    1. Lí thuyết

    a. Thiết diện cắt bởi mặt phẳng qua đỉnh của hình nón

    Thiết diện là một tam giác cân.

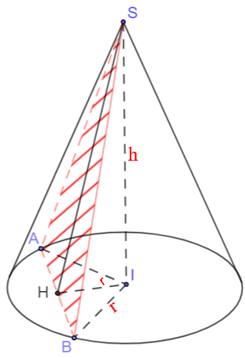
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Thiết diện là tam giác SAB cân tại S

    Gọi H là trung điểm AB. Khi đó:

    + Góc giữa thiết diện với đáy là SHI^. Giả sử SHI^=α⇒SH=hsinα

    IH=htanα⇒AH=IA2−IH2=r2−h2tan2α

    + Diện tích thiết diện:

    S△SAB=SH.AH=hsinα.r2−h2tan2α

    b. Thiết diện đi qua trục

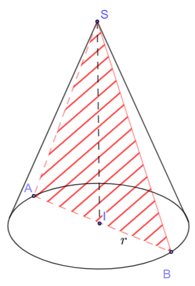
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Diện tích  thiết diện:

    SΔSAB=12SI.AB=h.r

    c. Thiết diện cắt bởi mặt phẳng vuông góc với trục

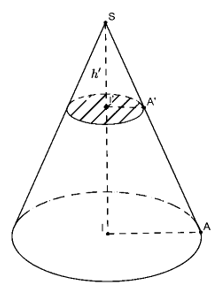
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Mặt phẳng (P) vuông góc và cách đỉnh một khoảng là h’ tạo ra thiết diện là một hình tròn.

    Ta có: 2 tam giác SI’A’ và SIA đồng dạng nên:

    SI'SI=I'A'IA⇔h'h=r'r⇒r'=rh.h'

    Diện tích thiết diện S=π.r'2

    2. Các ví dụ

    VD1. Một hình nón có thiết diện qua trục là một tam giác vuông cân cạnh a. Tính diện tích thiết diện đó.

    Lời giải:

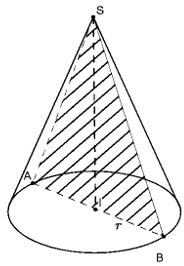
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Thiết diện là tam giác SAB

    Theo bài ta có SAB vuông cân tại S có SA=SB=a

    Diện tích tam giác SAB là 12SA.SB=12a2

    VD2. Cho hình nón có bán kính đáy bằng a2 và chiều cao bằng a3. Một mặt phẳng đi qua đỉnh tạo với mặt đáy góc 60∘. Tính diện tích thiết diện được tạo thành.

    Lời giải:

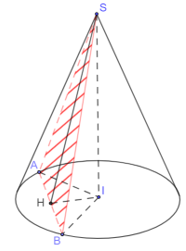
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Thiết diện tạo thành là tam giác SAB

    Gọi H là trung điểm AB. Ta chứng minh được SHI^=60∘

    ⇒IH=a3tan60∘=a

    SH=2a

    Tam giác IAH vuông tại H nên AH=IA2−IH2=a

    Suy ra SΔSAB=SH.AH=2a2

    VD3. Cho hình nón đỉnh S có chiều cao a. Mặt phẳng (P) qua S và cắt đáy tại A và B sao cho AB=2a3. Khoảng cách từ tâm đường tròn đáy đến (P) là a22. Tính diện tích thiết diện được tạo thành.

    Lời giải:

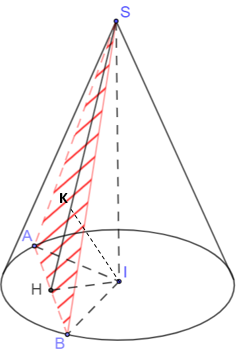
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Thiết diện là tam giác SAB

    Gọi H là trung điểm AB.

    Trong mp (SHI) kẻ IK⊥SH

    ⇒dISAB=IK=a22

    Ta có:

    1I​K2=1SI2+1IH2⇔2a2=1a2+1IH2​⇒IH=a⇒SH=SI2+IH2=a2

    Vậy diện tích thiết diện là S=12SH.AB=a26

    VD4. Cho hình nón có bán kính đáy bằng 3 và đường sinh là 5. Mặt phẳng (P) qua đỉnh và tạo với trục một góc 30∘. Tính diện tích thiết diện

    Lời giải:

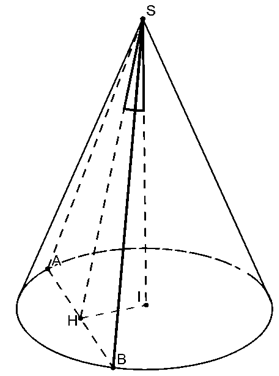
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Thiết diện là tam giác SAB

    Gọi H là trung điểm AB

    Ta có góc giữa (SAB) và trục là ISH^=30∘

    Chiều cao hình nón là :

    h=l2−r2=52−32=4

    ⇒IH=IH.tan30∘=433

    SH=833

    Ta có :

    AH=IA2−IH2=333⇒SΔSAB=SH.AH=8113

    VD5. Cho hình nón có bán kính đáy bằng 4 và chiều cao là 5. Mặt phẳng (P) vuông góc và cách đáy một đoạn bằng 2. Mặt phẳng (P) cắt hình nón theo giao tuyến là một đường tròn. Tính diện tích hình tròn đó.

    Lời giải:

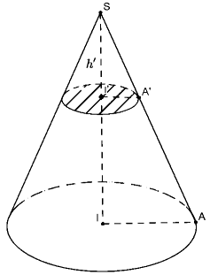
    Công thức tính diện tích thiết diện hình nón chi tiết nhất - Toán lớp 12 (ảnh 1)

    Gọi tâm thiết diện là I’ bán kính thiết diện là I’A’

    Tâm đường tròn đáy của nón là I; bán kính là IA

    Theo bài ta có II'=2⇒SI'=3

    Tam giác SI’A’ và SIA đồng dạng nên: 

    I'A'IA=SI'SI=35⇒r'=125

    Vậy diện tích thiết diện là:

    S=π.952=8125π

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 9,594 18/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: