Tích phân là gì? Tính chất, công thức, các dạng bài tập tích phân và cách giải

Tích phân là gì? Tính chất, công thức, các dạng bài tập tích phân và cách giải

1. Tích phần là gì?

Cho f là hàm số liên tục trên đoạn $\text{[}a;b\text{]}.$ Giả sử F là một nguyên hàm của f trên $\text{[}a;b\text{]}.$ Hiệu số $F\left(b\right)-F\left(a\right)$ được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn $\text{[}a;b\text{]}$ của hàm số $f\left(x\right),$ kí hiệu là $\underset{a}{\overset{b}{\int }}f\left(x\right)dx.$

Ta dùng kí hiệu ${\left.F\left(x\right)\right|}_a^b=F\left(b\right)-F\left(a\right)$ để chỉ hiệu số $F\left(b\right)-F\left(a\right)$.

Vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx={\left.F\left(x\right)\right|}_a^b=F\left(b\right)-F\left(a\right)$.

Ta gọi $\underset{a}{\overset{b}{\int }}$ là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

Chú ý: Trong trường hợp a = b hoặc a > b, ta quy ước $\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0$; $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)dx$.

Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ hay $\underset{a}{\overset{b}{\int }}f\left(t\right)dt.$Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.

Ý nghĩa hình học của tích phân: Nếu hàm số f liên tục và không âm trên đoạn $\text{[}a;b\text{]}$ thì tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số $y=f\left(x\right)$, trục Ox và hai đường thẳng x = a, x = b. Vậy $S=\underset{a}{\overset{b}{\int }}f\left(x\right)dx.$

2. Tính chất của tích phân

+) Tính chất 1: $\underset{a}{\overset{b}{\int }}kf\left(x\right)dx=k\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ với k là hằng số.

+) Tính chất 2: $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)\pm g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx\pm \underset{a}{\overset{b}{\int }}g\left(x\right)dx$

+) Tính chất 3: $\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\underset{c}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ với $a<c<b$.

Chú ý: Mở rộng của tính chất 3.

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{c_1}{\int }}f\left(x\right)dx+\underset{c_1}{\overset{c_2}{\int }}f\left(x\right)dx+\mathrm{...}\underset{c_n}{\overset{b}{\int }}f\left(x\right)dx \left(a<c_1<c_2<\mathrm{...}<c_n<b\right)$

+) $\underset{a}{\overset{b}{\int }}0dx=0$

+) $\underset{a}{\overset{b}{\int }}cdx=c\left(b-a\right)$

+) Nếu $f\left(x\right)\ge 0,\forall x\in \left[a,b\right]$ thì $\underset{a}{\overset{b}{\int }}f\left(x\right)dx\ge 0$

Hệ quả: Nếu hai hàm số $f\left(x\right)$ và $g\left(x\right)$ liên tục và thỏa mãn $f\left(x\right)\le g\left(x\right),\forall x\in \left[a;b\right]$

thì $\underset{a}{\overset{b}{\int }}f\left(x\right)dx\le \underset{a}{\overset{b}{\int }}g\left(x\right)dx$

3. Định lý nguyên hàm - tích phân

Ba định lý quan trọng về nguyên hàm và tích phân:

- Định lý 1: Giả sử chúng ta đã tìm thấy một nguyên hàm F(x) cho hàm số f(x) trên tập hợp K. Khi đó, cho mọi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x). Điều này có nghĩa rằng chúng ta có một không gian vô hạn các nguyên hàm của f(x), được xác định bởi hằng số C.

- Định lý 2: Trong tập hợp K, nếu F(x) là một nguyên hàm của hàm số f(x), thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số tùy ý. Điều này phản ánh sự đa dạng và tự do trong việc xây dựng nguyên hàm.

- Định lý 3: Trong tập hợp K, tất cả các hàm số f(x) liên tục đều có ít nhất một nguyên hàm. Điều này là một tuyên bố mạnh mẽ về tính tồn tại của nguyên hàm cho hàm số liên tục, đồng thời thể hiện tính chất quan trọng của nguyên hàm trong toán học và khoa học tự nhiên.

4. Cách tính tích phân

* Phương pháp đổi biến số:

- Phương pháp chung. Trong quá trình tích phân, chúng ta có thể sử dụng một phương pháp chung, được phân thành các bước cụ thể như sau:

+ Bước 1: Bắt đầu bằng việc đặt x = u(t).

+ Bước 2: Sau đó, chúng ta tính đạo hàm của cả hai bên của phương trình x = u(t), tức là dx = u'(t)dt.

+ Đổi cận: Sử dụng một biến đổi thích hợp để chuyển từ công thức ban đầu sang một biểu thức tích phân dựa trên biến t.

Như vậy, chúng ta thu được một biểu thức tích phân mới, chi tiết và đầy đủ, dựa trên sự biến đổi này. Phương pháp này là một công cụ quan trọng trong tích phân và nó có thể được áp dụng trong nhiều tình huống khác nhau để giải quyết các bài toán phức tạp.

- Phương pháp đổi biến loại 1 và cách áp dụng. Phương pháp đổi biến loại 1 là một công cụ mạnh mẽ trong tích phân và giúp giải quyết các bài toán tích phân khó khăn. Nó được áp dụng như sau:

+ Bước 1: Lựa chọn biến đổi. Đầu tiên, chúng ta lựa chọn một biến tương đương mới t = φ(x) sao cho đạo hàm của nó, φ'(t), dễ dàng tính toán và đối chiếu với đạo hàm của biểu thức cần tích phân. Tức là, chúng ta chọn t sao cho φ'(t) = u'(x), với u là hàm u(x) trong biểu thức cần tích phân.

+ Bước 2: Tính toán biến đổi. Sau đó, chúng ta thực hiện vi phân hai vế của biểu thức, tính toán dt = φ'(t)dx.

+ Bước 3: Biến đổi biểu thức. Biểu thức ban đầu ∫f[u(x)]u'(x)dx sau đó được biến đổi thành ∫f[φ(t)]dt, trong đó chúng ta đã sử dụng sự tương đương giữa u(x) và φ(t).

+ Kết quả cuối cùng: Cuối cùng, chúng ta đã biến đổi bài toán tích phân ban đầu thành một tích phân đơn giản hơn ∫f[φ(t)]dt. Từ đó, chúng ta có thể tích phân để tìm kết quả, và kết quả này có thể được biểu diễn bằng hàm G(t) + C, với G(t) là nguyên hàm của f[φ(t)].

Phương pháp đổi biến loại 1 giúp giảm bài toán tích phân phức tạp về một dạng dễ tính, đồng thời giúp hiểu rõ hơn về quá trình biến đổi trong tích phân.

- Phương pháp đổi biến loại 2 và cách sử dụng nó. Phương pháp đổi biến loại 2 là một công cụ mạnh mẽ trong tích phân, giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả. Cách áp dụng phương pháp này như sau:

+ Bước 1: Lựa chọn biến đổi. Trong bước này, chúng ta lựa chọn một biến đổi x = φ(t) sao cho nó thỏa mãn các điều kiện sau:

Hàm số f(x) cần tích phân phải liên tục trên tập hợp K.

Hàm số x = φ(t) là một biến đổi hợp lệ, tức là nó xác định và liên tục trên tập hợp K và có đạo hàm φ'(t).

+ Bước 2: Tính vi phân biến đổi. Sau đó, chúng ta thực hiện vi phân hai vế của biểu thức, tính toán dx = φ'(t)dt.

+ Bước 3: Biến đổi biểu thức. Biểu thức ban đầu ∫f(x)dx được biến đổi thành ∫f[φ(t)]φ'(t)dt, trong đó chúng ta đã sử dụng sự tương đương giữa x và φ(t).

+ Kết quả cuối cùng. Cuối cùng, chúng ta đã biến đổi bài toán tích phân ban đầu thành một tích phân đơn giản hơn ∫f[φ(t)]φ'(t)dt. Từ đó, chúng ta có thể tích phân để tìm kết quả, và kết quả này có thể được biểu diễn bằng hàm G(t) + C, với G(t) là nguyên hàm của f[φ(t)].

Phương pháp đổi biến loại 2 giúp chúng ta giải quyết bài toán tích phân một cách hiệu quả bằng cách biến đổi biến số và đơn giản hóa bài toán ban đầu. Điều này thường giúp chúng ta tiếp cận và giải quyết các bài toán tích phân khó khăn một cách hiệu quả hơn.

* Phương pháp tích phân từng phần

- Phương pháp chung tích phân. Trong việc tích phân một hàm số f(x), chúng ta có một phương pháp chung để giúp giải quyết bài toán này. Quá trình này được chia thành các bước cụ thể như sau:

+ Bước 1: Để bắt đầu, chúng ta chọn một phần thích hợp của hàm số f(x) để biểu diễn dưới dạng udv = u.v'dx, trong đó chúng ta lựa chọn một phần làm u(x) và phần còn lại là dv = v'(x)dx.

+ Bước 2: Tiếp theo, chúng ta tính giá trị của du = u'dx và thực hiện tích phân v = ∫dv = ∫v'(x)dx.

+ Bước 3: Cuối cùng, chúng ta sử dụng các giá trị đã tính ở bước 2 để tính toán...

5. Bảng công thức tích phân cơ bản

6. Ví dụ minh họa

Ví dụ 1. Tính $I=\underset{0}{\overset{1}{\int }}{\left(x^3-1\right)}^2{x}^{3}dx$ ta thu được kết quả là:

A. $\frac{8}{141}$

B. $\frac{9}{140}$

C. $\frac{140}{9}$

D. $\frac{141}{8}$

Lời giải

Ta có :

$$\begin{gathered} I=\underset{0}{\overset{1}{\int }}{\left(x^3-1\right)}^2{x}^{3}dx \\ =\underset{0}{\overset{1}{\int }}\left(x^6-2x^3+1\right)x^{3}dx \\ =\underset{0}{\overset{1}{\int }}\left(x^9-2x^6+x^3\right)dx \\ =\left(\frac{x^{10}}{10}-\frac{2x^7}{7}+\frac{x^4}{4}\right)\left|\begin{array}{l}1\\ 0\end{array}\right. \\ =\frac{1}{10}-\frac{2}{7}+\frac{1}{4}-0=\frac{9}{140} \end{gathered}$$

Chọn B.

Ví dụ 2: Tính tích phân $I=\underset{-2}{\overset{2}{\int }}|x+1|dx$.

Lời giải

Nhận xét:

$\left|x+1\right|=\left\{\begin{array}{l}x+1,-1\le x\le 2\\ -x-1,-2\le x<-1\end{array}\right..$

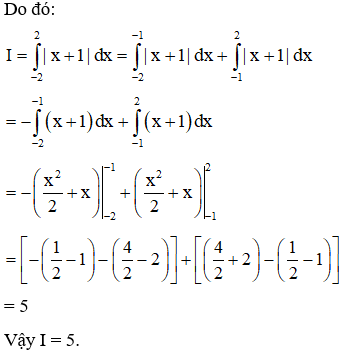
Ví dụ 3: Biết F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] và $3F\left(a\right)-2=3F\left(b\right)$. Tính tích phân $I=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

A. I = - 2

B. I = 2

C. $I=\frac{2}{3}$

D. $I=\frac{-2}{3}$

Lời giải

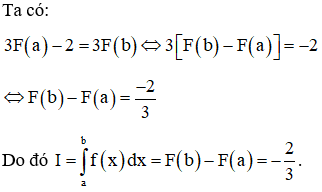
Chọn D

Ví dụ 4: Cho các tích phân $\underset{-3}{\overset{2}{\int }}f\left(x\right)dx=2;\underset{-3}{\overset{5}{\int }}f\left(t\right)dt=4$ . Tính $\underset{2}{\overset{5}{\int }}f\left(y\right)dy$.

A. I = 2

B. I = 6

C. I = - 2

D. I = - 6

Lời giải

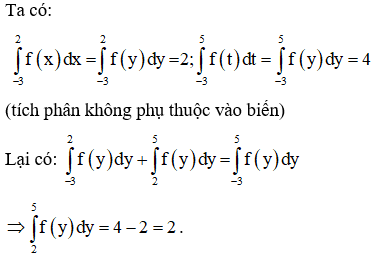
Chọn A.

Ví dụ 5: Cho $\underset{0}{\overset{\frac{\pi }{2}}{\int }}f\left(x\right)dx=5$ . Tính $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left[f\left(x\right)+2\sin x\right]dx$

A. I = 7

B. $I=5+\frac{\pi }{2}$

C. I = 3

D. $I=5+\pi$

Lời giải

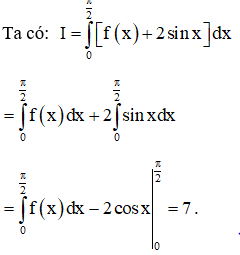
Chọn A.

7. Bài tập vận dụng

Câu 1. $\underset{2}{\overset{4}{\int }}{\left(x+\frac{1}{x}\right)}^{2}dx$ bằng:

A. $\frac{275}{12}$

B. $\frac{305}{16}$

C. $\frac{196}{15}$

D. $\frac{208}{17}$

Câu 2. $\underset{e-1}{\overset{e^2-1}{\int }}\frac{1}{x+1}dx$ bằng:

A. $3\left(e^2-e\right)$

B. 1

C. $\frac{1}{e^2}-\frac{1}{e}$

D. 2

Câu 3. $\underset{0}{\overset{\ln 2}{\int }}\left(e^x+1\right)e^{x}dx$ bằng:

A. $3\ln 2$

B. $\frac{4}{5}\ln 2$

C. $\frac{5}{2}$

D. $\frac{7}{3}$

Câu 4. $\underset{0}{\overset{4}{\int }}\frac{1}{\sqrt{2x+1}}dx$ bằng:

A. 5

B. 4

C. 3

D. 2

Câu 5. $\underset{2}{\overset{5}{\int }}{\left(3x-4\right)}^{4}dx$ bằng:

A. $\frac{89720}{27}$

B. $\frac{18927}{20}$

C. $\frac{960025}{18}$

D. $\frac{53673}{5}$

Câu 6. Kết quả của tích phân: $I=\underset{0}{\overset{1}{\int }}\frac{7+6x}{3x+2}dx$

A. $\frac{1}{2}-\ln \frac{5}{2}$

B. $\ln \frac{5}{2}$

C. 2+ $\ln \frac{5}{2}$

D. $3+2\ln \frac{5}{2}$

Câu 7. Tích phân: $\underset{0}{\overset{4}{\int }}\left|x-2\right|dx$

A. 0

B. 2

C. 8

D. 4

Câu 8. Tích phân $\underset{0}{\overset{2}{\int }}\left|x^2-x\right|dx$ bằng

A. $\frac{2}{3}$

B. 0

C. 1

D. $\frac{3}{2}$

Câu 9. Tính $\underset{-1}{\overset{2}{\int }}\frac{dx}{1+\left|1-x\right|}$?

A. 2ln3

B. ln3

C. ln2

D. ln6

Câu 10. Nếu${\int }_1^{4}f\left(x\right)dx=6$ và ${\int }_1^4 g\left(x\right)dx=-5$ thì ${\int }_1^4\left[f\right(x)-g(x\left)\right]$ bằng

A. -1.

B. -11.

C. 1.

D. 11.

Câu 11. Cho biết $\underset{2}{\overset{5}{\int }}f\left(x\right)dx=3$, $\underset{2}{\overset{5}{\int }}g\left(x\right)dx=9$. Giá trị của $A=\underset{2}{\overset{5}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx$ là:

A. Chưa xác định được

B. 12

C. 3

D. 6

Câu 12. Cho $2I={\int }_1^2(2x^3+\ln x)dx$. Tìm I?

A. $1+2\ln 2$

B. $\frac{13}{2}+2\ln 2$

C. $\frac{13}{4}+\ln 2$

D. $\frac{1}{2}+\ln 2$

Câu 13. Nếu $\underset{0}{\overset{10}{\int }}f\left(x\right)dx=17$ và $\underset{0}{\overset{8}{\int }}f\left(x\right)dx=12$ thì $\underset{8}{\overset{10}{\int }}f\left(x\right)dx$ bằng:

A. 5

B. 29

C. - 5

D. 15

Câu 14. f và g là hai hàm số theo x. Biết rằng $\forall x\in [a,b],f\text{'}\left(x\right)=g\text{'}\left(x\right)$

Trong các mệnh đề:

(I) $\forall x\in [a,b],f\text{'}\left(x\right)=g\left(x\right)$

(II) $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{b}{\int }}g\left(x\right)dx$

(III) $\forall x\in [a;b],f\left(x\right)-f\left(a\right)=g\left(x\right)-g\left(a\right)$

Mệnh đề nào đúng?

A. I

B. II

C. Không có

D. III

Câu 15. Để $\underset{1}{\overset{k}{\int }}\left(k-4x\right)dx+3k+1=0$ thì giá trị của k là bao nhiêu ?

A. 1

B. 3

C. 2

D. 4

Câu 16. Nếu $\underset{0}{\overset{6}{\int }}f\left(x\right)dx=10$ và $\underset{0}{\overset{4}{\int }}f\left(x\right)dx=7$, thì $\underset{4}{\overset{6}{\int }}f\left(x\right)dx$ bằng:

A. 3

B. 17

C. 170

D. - 3

Câu 17. Tìm a sao cho $I=\underset{1}{\overset{2}{\int }}{\text{[a}}^{\text{2}}{\text{+(4 - a)x + 4x}}^{\text{3}}\text{]dx = 12}$

A. Đáp án khác

B. a = - 3

C. a = 5

D. a = 3

Câu 18. Biết $\underset{0}{\overset{b}{\int }}\left(2x-4\right)dx=0$, khi đó b nhận giá trị bằng:

A. $b=1$ hoặc $b=4$

B. $b=0$ hoặc $b=2$

C. $b=1$ hoặc $b=2$

D. $b=0$ hoặc $b=4$

Câu 19. Cho $\underset{0}{\overset{1}{\int }}{e}^{3x}dx=\frac{e^a-1}{b}$. Khi đó khẳng định nào sau đây là đúng

A. a = - b

B. a < b

C. a > b

D. a = b

Câu 20. Nếu $\underset{a}{\overset{d}{\int }}f\left(x\right)dx=5$; $\underset{b}{\overset{d}{\int }}f\left(x\right)dx=2$, với $a<d<b$ thì $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ bằng:

A. - 2

B. 3

C. 8

D. 0

Câu 21. Cho tích phân $I=\underset{0}{\overset{3}{\int }}\left|2^x-4\right|dx$, trong các kết quả sau:

(I). $I=\underset{2}{\overset{3}{\int }}\left(2^x-4\right)dx+\underset{0}{\overset{2}{\int }}\left(2^x-4\right)dx$

(II). $I=\underset{2}{\overset{3}{\int }}\left(2^x-4\right)dx-\underset{0}{\overset{2}{\int }}\left(2^x-4\right)dx$

(III). $I=2\underset{2}{\overset{3}{\int }}\left(2^x-4\right)dx$

Kết quả nào đúng?

A. Chỉ II.

B. Chỉ III

C. Cả I, II, III.

D. Chỉ I.

Câu 22. Cho hàm số y = f(x) liên tục và chỉ triệt tiêu khi x = c trên [a; b]. Các kết quả sau, câu nào đúng?

A. $\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx\ge \left|\underset{a}{\overset{b}{\int }}f\left(x\right)dx\right|$

B. $\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx=\underset{a}{\overset{c}{\int }}\left|f\left(x\right)\right|dx+\underset{c}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$

C. $\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx=\left|\underset{a}{\overset{c}{\int }}\left|f\left(x\right)\right|dx\right|+\left|\underset{a}{\overset{b}{\int }}f\left(x\right)dx\right|$

D. A, B, C đều đúng

Câu 23. Khẳng định nào sau đây sai về kết quả $\underset{-1}{\overset{0}{\int }}\left|\frac{x+1}{x-2}\right|dx=a\ln \frac{b}{c}-1$ ?

A. $a.b=3(c+1)$

B. $ac=b+3$

C. $a+b+2c=10$

D. $ab=c+1$

Câu 24. Cho f(x) là hàm số chẵn và liên tục trên R thỏa mãn $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=2$. Khi đó giá trị tích phân $\underset{0}{\overset{1}{\int }}f\left(x\right)dx$ là:

A. 2

B. 1

C. $\frac{1}{2}$

D. $\frac{1}{4}$

Câu 25. Cho hàm số f liên tục trên đoạn [a; b] có một nguyên hàm là hàm F trên đoạn [a; b]. Trong các phát biểu sau, phát biểu nào sai ?

A. $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=F\left(b\right)-F\left(a\right)$

B. $F\text{'}\left(x\right)=f\left(x\right)$ với mọi $x\in (a;b)$.

C. $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=f\left(b\right)-f\left(a\right)$.

D. Hàm số G cho bởi $G\left(x\right)=F\left(x\right)+5$ cũng thỏa mãn $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=G\left(b\right)-G\left(a\right)$.

Câu 26. Cho hai hàm số f và g liên tục trên đoạn [a; b] sao cho $g\left(x\right)\ne 0$ với mọi $x\in [a;b]$. Xét các khẳng định sau:

I. $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}g\left(x\right)dx$.

II. $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx-\underset{a}{\overset{b}{\int }}g\left(x\right)dx$.

III. $\underset{a}{\overset{b}{\int }}\left[f\left(x\right).g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx.\underset{a}{\overset{b}{\int }}g\left(x\right)dx$.

IV. $\underset{a}{\overset{b}{\int }}\frac{f\left(x\right)}{g\left(x\right)}dx=\frac{{\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}}{{\displaystyle \underset{a}{\overset{b}{\int }}g\left(x\right)dx}}$.

Trong các khẳng định trên, có bao nhiêu khẳng định sai?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 27. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu f là hàm số chẵn trên R thì $\underset{0}{\overset{1}{\int }}f\left(x\right)dx=\underset{-1}{\overset{0}{\int }}f\left(x\right)dx$.

B. Nếu $\underset{-1}{\overset{0}{\int }}f\left(x\right)dx=\underset{0}{\overset{1}{\int }}f\left(x\right)dx$ thì f là hàm số chẵn trên đoạn $[-1;1]$

C. Nếu $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=0$ thì f là hàm số lẻ trên đoạn $[-1;1]$

D. Nếu $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=0$ thì f là hàm số chẵn trên đoạn $[-1;1]$

Câu 28. Tích phân $\underset{0}{\overset{2}{\int }}k{e}^{x}dx$ (với k là hằng số )có giá trị bằng:

A. $k(e^2-1)$

B. $e^2-1$

C. $k(e^2-e)$

D. $e^2-e$

Câu 29. Tích phân $\underset{-1}{\overset{5}{\int }}\left|x^2-2x-3\right|dx$ có giá trị bằng

A. 0

B. $\frac{64}{3}$

C. 7.

D. 12,5.

Câu 30. Giá trị của a để đẳng thức $\underset{1}{\overset{2}{\int }}\left[a^2+(4-4a)x+4x^3\right]dx=\underset{2}{\overset{4}{\int }}2xdx$ là đẳng thức đúng

A. 4.

B. 3.

C. 5

D. 6.

Đáp án