Nội dung bài viết

    Xem thêm

    Công thức tính thể tích khối tròn xoay (đầy đủ, chính xác nhất)

    Với Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất Toán lớp 12 Giải tích chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất biết cách làm bài tập Toán 12. Mời các bạn đón xem:

    1 8,988 04/09/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức tính thể tích khối tròn xoay (đầy đủ, chính xác nhất)

    1. Lý thuyết khối tròn xoay

    Khối tròn xoay là một khối hình được tạo bằng cách quay một mặt phẳng quanh một trục cố định. Trong chương trình toán học phổ thông các bạn sẽ được tiếp xúc với một số khối tròn xoay như khối nón tròn xoay, khối trụ tròn xoay, khối cầu tròn xoay,...

    2. Công thức tính thể tích khối tròn xoay

    * Quay quanh trục Ox:

    Hình giới hạn bởi đường cong y = f(x), trục Ox và hai đường thẳng x = a, x = b (trong đó f(x) liên tục trên đoạn [a;b]) quay quanh trục Ox, ta được khối tròn xoay.

    Thể tích của khối tròn xoay được tính theo công thức: V=π∫abfx2dx

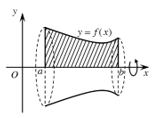
    Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

    Hình giới hạn bởi hai đường cong y = f(x), y = g(x) và hai đường thẳng x = a, x = b (trong đó f(x), g(x) liên tục trên đoạn [a;b]) quay quanh trục Ox.

    Thể tích của khối tròn xoay được tính theo công thức: V=π∫abf2x−g2xdx

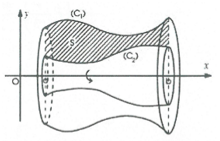
    Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

    * Quay quanh trục Oy:

    Hình giới hạn bởi đường cong x = f(y), trục Oy và hai đường thẳng y = c; y = d (trong đó f(x) liên tục trên đoạn [c; d]) quay quanh trục Oy, ta được khối tròn xoay.

    Thể tích của khối tròn xoay được tính theo công thức: V=π∫abfy2dy

    Ví dụ 1: Tính thể tích của khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi các đường y = sin x, trục hoành, hai đường thẳng x=0;x=π4 quay quanh trục hoành?

    Lời giải

    Hình phẳng giới hạn bởi các đường y=sinx;   y=0;   x=0;   x=π4 quay quanh trục Ox nên có thể tích:

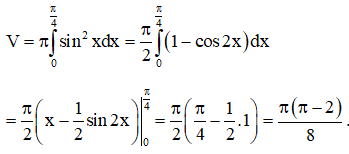
    Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

    Ví dụ 2: Cho hình phẳng H giới hạn bởi các đường: y=x;  y=x. Tính thể tích khối tròn xoay được tạo thành khi quay H quanh trục hoành?

    Lời giải

    Phương trình hoành độ giao điểm của hai đường:

    x=x⇒x=0x=1

    Thể tích khối tròn xoay được tạo bởi hai đường y=x;  y=x là:

    V=π∫01x2−x2dx=π∫01x2−xdx=πx33−x2201=π13−12=π6

    3. Bài tập vận dụng

    Bài 1: Thể tích của khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong y = sinx, trục hoành và hai đường thẳng (hình vẽ) quanh trục Ox là

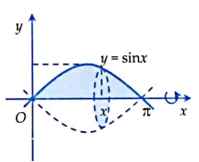
    Ứng dụng của tích phân tính thể tích khối tròn xoay và cách giải – Toán lớp 12 (ảnh 1)

    Giải

    Áp dụng công thức ở định lý trên ta có

    V=π∫0πsin2xdx=π2∫0π1−cos2xdx=π2x−12sin2x0π=π2π−12sin2π−π20−12sin0=π22

    Bài 2: Tính thể tích khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong y=A2−x2 và trục hoành quanh trục hoành.

    Ứng dụng của tích phân tính thể tích khối tròn xoay và cách giải – Toán lớp 12 (ảnh 1)

    Giải:

    Ta thấy:

    y=A2−x2⇔y2=A2−x2⇔x2+y2=A2

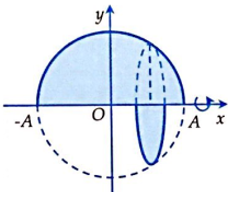
    Do A2−x2≥0 với mọi x, do vậy đây là phương trình nửa đường tròn tâm O, bán kính R = A nằm phía trên trục Ox. Khi quay quanh trục Ox thì hình phẳng sẽ tạo nên một khối cầu tâm O, bán kính R = A (hình vẽ). Do vậy ta có luôn V=43.π.A3

    Vậy với bài toán dạng này, ta không cần viết công thức tích phân mà kết luận luôn theo công thức tính thể tích khối cầu.

    Bài 3: Cho hình phẳng (H) giới hạn bởi các đường . Tính thể tích V của khối tròn xoay thu được khi quay (H) quanh trục Ox.

    Giải

    Thể tích cần tính là:

    V=π∫02x4dx=π.x5502=32π5.

    Bài 4: Tính thể tích hình khối do hình phẳng giới hạn bởi các đường quay quanh Oy.

    Giải:

    Ứng dụng của tích phân tính thể tích khối tròn xoay và cách giải – Toán lớp 12 (ảnh 1)

    Bài 5: Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 1, biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ là một hình chữ nhật có độ dài hai cạnh là x và .

    Giải:

    Do thiết diện là hình chữ nhật nên diện tích thiết diện là:

    Sx=xlnx2+1

    Ta có thể tích cần tính là

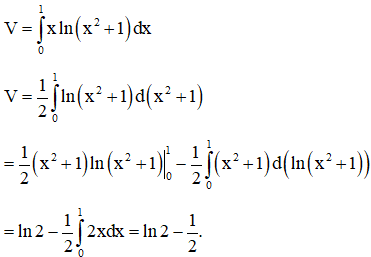
    Ứng dụng của tích phân tính thể tích khối tròn xoay và cách giải – Toán lớp 12 (ảnh 1)

    Bài 6: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số y = f(x) trục Ox và hai đường thẳng x = a, x = b (a < b) xung quanh trục Ox.

    Bài 7: Cho hình phẳng D giới hạn bởi đường cong , trục hoành và các đường thẳng x = 0; x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?

    Bài 8: Cho hình phẳng (H) giới hạn bởi các đường , và x = 4. Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành nhận giá trị nào?

    Bài 9: Thể tích của khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi (C): y = lnx, trục Ox và đường thẳng x = e là

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 8,988 04/09/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: