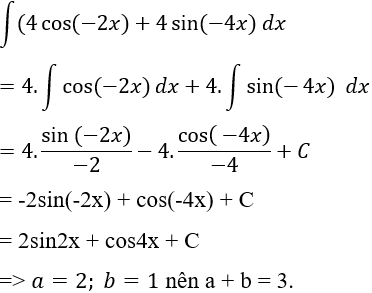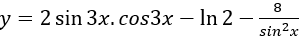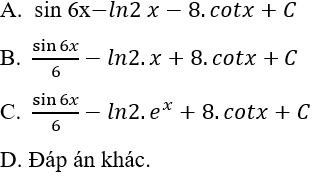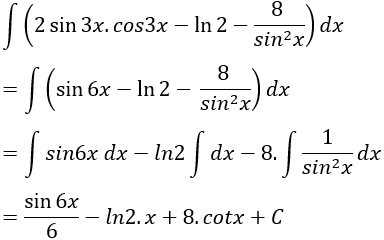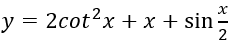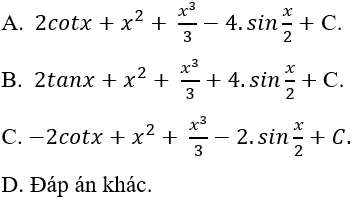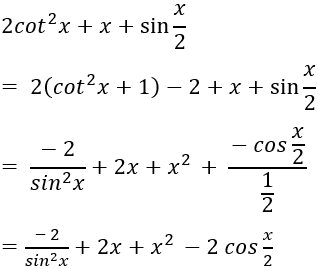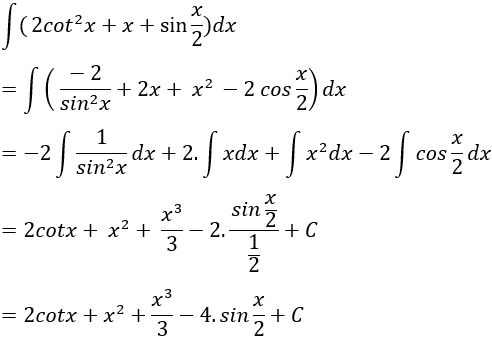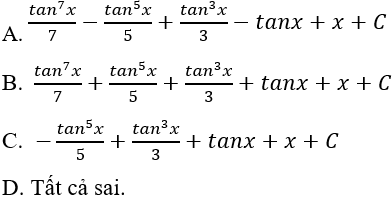Công thức nguyên hàm lượng giác. Cách tìm nguyên hàm lượng giác (chính xác nhất)
Với Công thức nguyên hàm hàm lượng giác chi tiết nhất Toán lớp 12 Giải tích chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ Công thức nguyên hàm hàm lượng giác chi tiết nhất biết cách làm bài tập Toán 12. Mời các bạn đón xem:
Công thức nguyên hàm hàm lượng giác chi tiết nhất - Toán lớp 12
I. Bảng công thức nguyên hàm của hàm số lượng giác
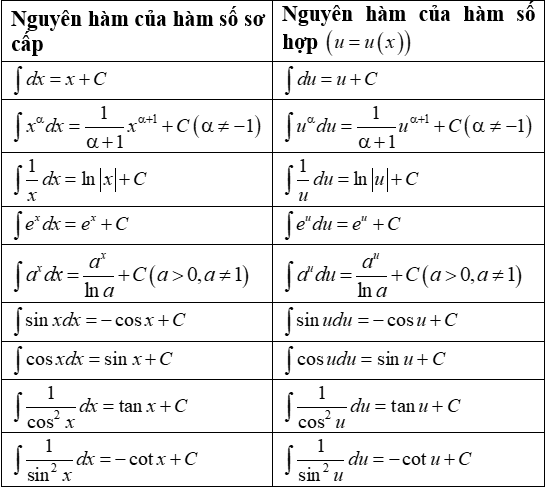
Một số biến đổi lượng giác cơ bản:
Công thức hạ bậc hai
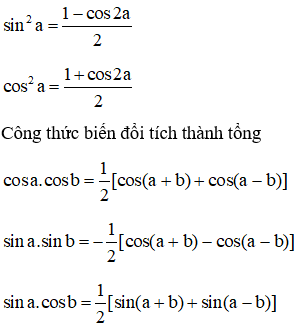
Ví dụ 1: Tính các nguyên hàm sau
a)
b)
c)
Lời giải
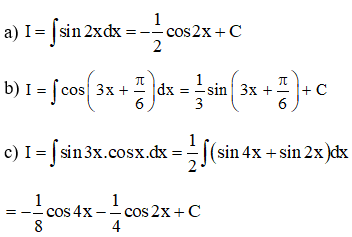
Ví dụ 2: Tính các nguyên hàm sau:
a)
b)
c)
Lời giải
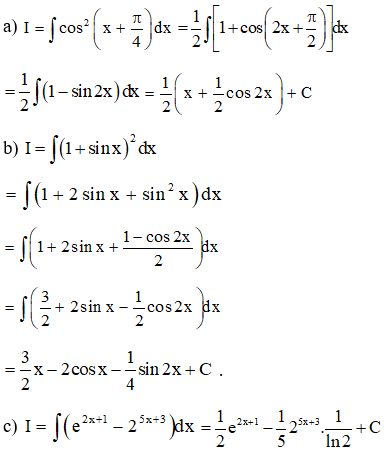
II. Các dạng bài tập và phương pháp giải
1. Dạng trong đó m, n là các số tự nhiên
Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.
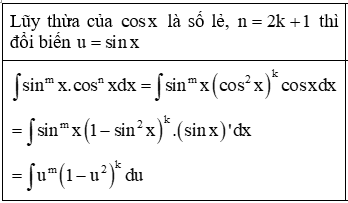
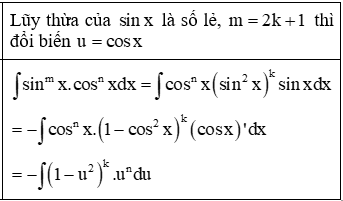
Trường hợp 2: Cả hai số m, n đều là số chẵn: Ta sử dụng công thức hạ bậc để giảm một nửa số mũ của , để làm bài toán trở nên đơn giản hơn.
2. Dạng ;
; ;
.
Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác.
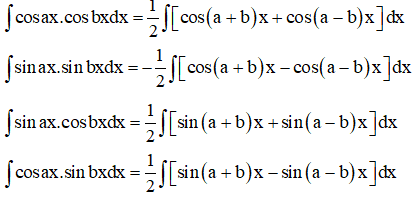
3. Dạng trong đó m, n là các số nguyên

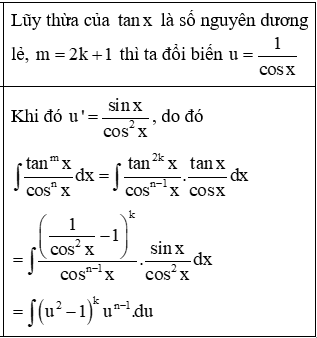
4. Đổi biến số với hàm lượng giác
Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng , thì ta có cách biến đổi lượng giác như sau:

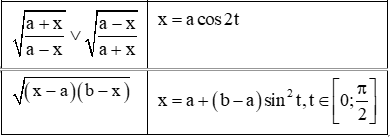
III. Bài tập vận dụng
Câu 1: Nguyên hàm của hàm số y = 4.cos(-2x) + 4sin(-4x) có dạng F(x) = a.sin2x + b.cos4x. Tính a + b?
A. –1.
B. 3.
C. 2.
D. -2.
Lời giải:
Ta có nguyên hàm của hàm số đã cho là:
Chọn B.
Câu 2: Tìm nguyên hàm của hàm số:
Lời giải:
Ta có:
Nguyên hàm của hàm số đã cho là:
Chọn B.
Câu 3: Tìm nguyên hàm của hàm số sau:
Lời giải:
Ta có:
⇒ Nguyên hàm của hàm số đã cho là:
Chọn A.
Câu 4: Tìm nguyên hàm của hàm số y = tan8x.dx
Lời giải:
Ta có nguyên hàm của hàm số đã cho là:
∫tan8x dx = ∫[tan6x.(1 + tan2x) - tan4(1 + tan2x) + tan2x.(1 + tan2x) - (1 + tan2x) + 1]dx
= ∫(tan6x - tan4x + tan2 - 1)dtanx + ∫dx.
Chọn D.
Câu 5. Tìm công thức sai:
A.
B.
C.
D.
Câu 6. Tìm nguyên hàm của: với là:
A.
B.
C.
D.
Câu 7. bằng:
A.
B. -4
C. 4
D. 2
Câu 8. bằng:
A.
B.
C.
D.
Câu 9. bằng:
A.
B.
C.
D.
Xem thêm tổng hợp công thức môn Toán lớp 12 đầy đủ và chi tiết khác:
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12