Nội dung bài viết

    Xem thêm

    Công thức tính GTNN - GTLN của hàm số chi tiết nhất – Toán 12

    Với Công thức tính GTNN - GTLN của hàm số chi tiết nhất Toán lớp 12 Giải tích chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ Công thức tính GTNN - GTLN của hàm số chi tiết nhất biết cách làm bài tập Toán 12. Mời các bạn đón xem:

    1 5,415 18/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức tính GTNN - GTLN của hàm số chi tiết nhất - Toán lớp 12

    1. Lí thuyết

    - Định nghĩa: Cho hàm số y=fx xác định trên tập D

    a. Số M được gọi là giá trị lớn nhất của hàm số y=fx trên D nếu fx≤M ∀x∈D và tồn tại x0∈D:fx0=M

    - Kí hiệu là: M=maxDfx

    b. Số m được gọi là giá trị nhỏ nhất của hàm số y=fx trên D nếu fx≥M ∀x∈D và tồn tại x0∈D:fx0=m

    - Kí hiệu là: m=minDfx

    2. Các bước tìm GTLN - GTNN của hàm số trên D hoặc trên một khoảng xác định.

    - Tìm TXĐ: D

    - Tính y'. Tìm những điểm mà y'=0 và y' không xác định

    - Lập bảng biến thiên

    - Dựa vào bảng biến thiên và kết luận GTLN; GTNN

    - Lưu ý: GTLN, GTNN của hàm số phải là số hữu hạn

    + Trong một vài TH (thường là hàm phân thức) GTLN, GTNN hữu hạn nhưng đạt tại x=±∞. Khi đó ta cũng kết luận là hàm số không có GTLN (GTNN).

    3. Cách tính GTLN và GTNN trên một đoạn

    a. Định lí: Mọi hàm số liên tục trên một đoạn đều có GTLN và GTNN trên đoạn đó.

    b. Quy tắc tìm GTLN, GTNN trên đoạn [a,b]

    - Tìm các điểm x1,x2,...xn trên khoảng a;b mà tại đó f'x=0 hoặc f'x không xác định

    - Tính fa,fx1,fx2,...fxn,fb.

    - Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.

    - Kết luận: maxa;bfx=M và mina;bfx=m

    - Chú ý: Đối với hàm phân thức y=ax+bcx+d. Khi tìm GTLN và GTNN của hàm này trên đoạn m;n.

    +) Nếu −dc∈m;n thì hàm số không có GTLN và GTNN

    +) Nếu −dc∉m;n thì GTLN và GTNN sẽ đạt tại các đầu mút.

    4. Các ví dụ

    VD1. Tìm GTLN và GTNN của các hàm số sau:

    a. y=x−3+1x  trên khoảng 0;+∞

    b. y=x4+x2 trên khoảng −∞;+∞

    Lời giải:

    a. Trên khoảng 0;+∞, ta có: y'=1−1x2;y'=0⇔x=1

    Bảng biến thiên

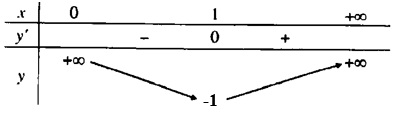
    Công thức tính GTNN - GTLN của hàm số chi tiết nhất - Toán lớp 12 (ảnh 1)

    Từ bảng biến thiên ta thấy min0;+∞y=y1=−1 và không tồn tại GTNN.

    b. y'=4+x2−2x24+x22=4−x24+x22.

    y'=0⇔x=±2

    Bảng biến thiên:

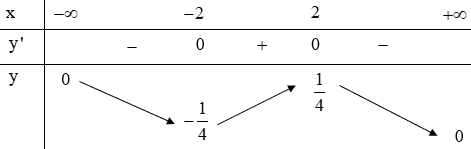
    Công thức tính GTNN - GTLN của hàm số chi tiết nhất - Toán lớp 12 (ảnh 1)

    Dựa vào bảng biến thiên ta thấy maxy=y2=14 và miny=y−2=−14

    VD2. Tìm GTLN, GTNN của các hàm số sau:

    a. y=x3+3x2−9x−7 trên đoạn −4;3

    b. y=x4−4x2+3 trên đoạn 1;3

    Lời giải:

    a.

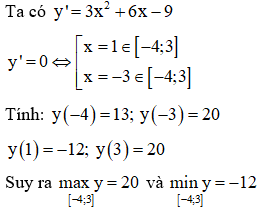
    Công thức tính GTNN - GTLN của hàm số chi tiết nhất - Toán lớp 12 (ảnh 1)

    b. 

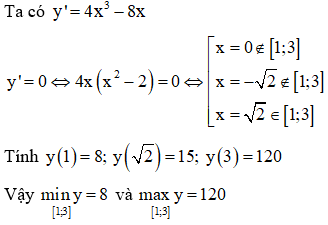
    Công thức tính GTNN - GTLN của hàm số chi tiết nhất - Toán lớp 12 (ảnh 1)

    5. Luyện tập

    Bài 1. Tìm GTLN và GTNN của hàm số:

    a. y=2x3−3x2−12x+8 trên đoạn −3;3

    b. y=x4−2x2+3 trên đoạn −2;0

    c. y=x−1x−2 trên đoạn −4;4

    Bài 2. Tìm GTLN, GTNN của các hàm số sau:

    a. y=1sinx trên đoạn π3;5π6

    b. y=x3−3x2−9x+35 trên các đoạn −4;4 và −5;3

    Bài 3. Tìm GTLN, GTNN các hàm số sau:

    a. y=x2−3x+3x−1

    b. 11+x4

    Bài 4. Tìm hai số có hiệu là 13 sao cho tích của chúng bé nhất.

    Bài 5. Một chất điểm chuyển động theo phương trình x=6t2−t3. Tính thời điểm t (giây) mà tại đó chất điểm có vận tốc lớn nhất.

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 5,415 18/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: